Solves a linear programming problem.
Synopsis
#include <imsl.h>
double
*imsl_d_linear_programming (int
m, int n, double
a[],
double
b[],
double c[], ¼, 0)
Required Arguments
int m
(Input)
Number of constraints.
int n
(Input)
Number of variables.
double a[]
(Input)
Array of size m ´ n containing a matrix with
coefficients of the m constraints.
double b[]
(Input)
Array with m components
containing the right-hand side of the constraints; if there are limits on both
sides of the constraints, then b contains the lower
limit of the constraints.
double c[]
(Input)
Array with n components
containing the coefficients of the objective function.
Return Value
A pointer to the solution x of the linear programming problem. To release this space, use free. If no solution can be computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
double
*imsl_d_linear_programming (int
m, int n, double
a[],
double
b[],
double
c[],
IMSL_A_COL_DIM, int
a_col_dim,
IMSL_UPPER_LIMIT, double
bu[],
IMSL_CONSTR_TYPE, int
irtype[],
IMSL_LOWER_BOUND, double
xlb[],
IMSL_UPPER_BOUND, double
xub[],
IMSL_REFINEMENT,
IMSL_EXTENDED_REFINEMENT,
IMSL_OBJ, double
*obj,
IMSL_RETURN_USER, double
x[],
IMSL_DUAL, double
**y,
IMSL_DUAL_USER, double
y[],
0)
Optional Arguments
IMSL_A_COL_DIM, int a_col_dim
(Input)
The column dimension of a.
Default: a_col_dim = n
IMSL_UPPER_LIMIT, double bu[]
(Input)
Array with m components
containing the upper limit of the constraints that have both the lower and the
upper bounds. If no such constraint exists, then
bu is not needed.
IMSL_CONSTR_TYPE, int irtype[]
(Input)
Array with m components
indicating the types of general constraints in the matrix a. Let ri = ai1x1 + ¼ + ainxn. Then, the value
of irtype[I] signifies the
following:
|
Irtype[I] |
Constraint |
|
0 |
ri = bi |
|
1 |
ri £ bui |
|
2 |
ri ³ bi |
|
3 |
bi £ ri £ bui |
|
4 |
Ignore this constraint |
Default: irtype = 0
IMSL_LOWER_BOUND, double xlb[]
(Input)
Array with n components
containing the lower bound on the variables. If there is no lower bound on a
variable, then 1030 should be set as the lower
bound.
Default: xlb = 0
IMSL_UPPER_BOUND,
double xub[]
(Input)
Array with n components
containing the upper bound on the variables. If there is no upper bound on a
variable, then −1030 should be
set as the upper bound.
Default: no upper bound
IMSL_REFINEMENT
(Input)
The coefficient matrices and other data are saved at the
beginning of the computation. When finished this data together with the
solution obtained is checked for consistency. If the discrepancy is too large,
the solution process is restarted using the problem data just after processing
the equalities, but with the final x values and final
active set.
Default: Refinement is not performed.
IMSL_EXTENDED_REFINEMENT
(Input)
This is similar to IMSL_REFINEMENT,
except it iterates until there is a sign that no further progress is possible
(recommended if all the accuracy possible is desired) .
Default:
Extended refinement is not performed.
IMSL_OBJ, double *obj
(Output)
Optimal value of the objective function.
IMSL_ITERATION_COUNT, int
*iterations (Output)
Number of iterations.
IMSL_RETURN_USER, double x[]
(Output)
Array with n components
containing the primal solution.
IMSL_DUAL, double **y
(Output)
The address of a pointer y to an array with
m components
containing the dual solution. On return, the necessary space is allocated by
imsl_d_linear_programming.
Typically, double *y is declared, and
&y is used
as an argument.
IMSL_DUAL_USER, double y[]
(Output)
A user-allocated array of size m. On return, y contains the dual
solution.
Description
The function imsl_d_linear_programming uses an active set strategy to solve linear programming problems, i.e., problems of the form
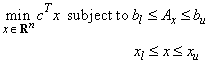
where c is the objective coefficient vector, A is the coefficient matrix, and the vectors bl, bu, xl, and xu are the lower and upper bounds on the constraints and the variables, respectively.
Examples
Example 1
The linear programming problem in the standard form

is solved.
#include
<imsl.h>
main()
{
int m = 4;
int n = 6;
double a[ ] = {1.0, 1.0, 1.0, 0.0,
0.0, 0.0,
1.0, 1.0, 0.0, -1.0, 0.0,
0.0,
1.0, 0.0, 0.0, 0.0, 1.0,
0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 1.0};
double b[ ]
= {1.5, 0.5, 1.0, 1.0};
double c[ ] = {-1.0, -3.0, 0.0, 0.0, 0.0,
0.0};
double
*x;
/* Solve the LP problem */
x = imsl_d_linear_programming
(m, n, a, b, c,
0);
/* Print x */
imsl_d_write_matrix
("x", 1, 6, x, 0);
}
Output
x
1
2
3
4
5
6
0.5 1.0
0.0
1.0
0.5 0.0
Example 2
This example demonstrates how the function imsl_d_read_mps can be used together with imsl_d_linear_programming to solve a linear programming problem defined in an MPS file. The MPS file used in this example is an uncompressed version of the file ‘afiro’, available from http://www.netlib.org/lp/data/. This example also demonstrates the use of the optional argument IMSL_REFINEMENT to activate iterative refinement in imsl_d_linear_programming.
#include <stdio.h>
#include <malloc.h>
#include <imsl.h>
void main()
{
#define A(I, J) a[(I)*problem->ncolumns+J]
Imsl_d_mps* problem;
int i, j, k, *irtype;
double *x, objective, *a, *b, *bl, *bu, *xlb, *xub;
/* Read the MPS file. */
problem = imsl_d_read_mps("afiro", 0);
/*
* Setup constraint type array.
*/
irtype = (int*)malloc(problem->nrows*sizeof(int));
for (i = 0; i < problem->nrows; i++)
irtype[i] = 3;
/*
* Setup the constraint matrix.
*/
a = (double*)calloc(problem->nrows*problem->ncolumns*sizeof(double),
sizeof(double));
for (k = 0; k < problem->nonzeros; k++) {
i = problem->constraint[k].row;
j = problem->constraint[k].col;
A(i, j) = problem->constraint[k].val;
}
/*
* Setup constraint bounds.
*/
bl = (double*)malloc(problem->nrows*sizeof(double));
bu = (double*)malloc(problem->nrows*sizeof(double));
for (i = 0; i < problem->nrows; i++) {
bl[i] = problem->lower_range[i];
bu[i] = problem->upper_range[i];
}
/*
* Setup variable bounds. Be sure to account for
* how unbounded variables should be set.
*/
xlb = (double*)malloc(problem->ncolumns*sizeof(double));
xub = (double*)malloc(problem->ncolumns*sizeof(double));
for (i = 0; i < problem->ncolumns; i++) {
xlb[i] = (problem->lower_bound[i] == problem->negative_infinity)?
1.0e30:problem->lower_bound[i];
xub[i] = (problem->upper_bound[i] == problem->positive_infinity)?
-1.0e30:problem->upper_bound[i];
}
/*
* Solve the LP problem.
*/
x = imsl_d_linear_programming(problem->nrows, problem->ncolumns,
a, bl, problem->objective,
IMSL_UPPER_LIMIT, bu,
IMSL_CONSTR_TYPE, irtype,
IMSL_LOWER_BOUND, xlb,
IMSL_UPPER_BOUND,
xub,
IMSL_REFINEMENT,
IMSL_OBJ, &objective,
0);
/*
* Output results.
*/
printf("Problem Name: %s\n", problem->name);
printf("objective : %e\n", objective);
imsl_d_write_matrix("Solution", problem->ncolumns, 1, x, 0);
/*
* Free memory.
*/
imsl_d_mps_free(problem);
free(irtype);
free(a);
free(bu);
free(bu);
free(xlb);
free(xub);
}
Output
Problem Name: AFIRO
objective : -4.647531e+02
Solution
1 80.0
2 25.5
3 54.5
4 84.8
5 57.9
6 0.0
7 0.0
8 0.0
9 0.0
10 0.0
11 0.0
12 0.0
13 18.2
14 39.7
15 61.3
16 500.0
17 475.9
18 24.1
19 0.0
20 215.0
21 363.9
22 0.0
23 0.0
24 0.0
25 0.0
26 0.0
27 0.0
28 0.0
29 339.9
30 20.1
31 156.5
32 0.0
Note Errors
IMSL_MULTIPLE_SOLUTIONS Multiple solutions giving essentially the same minimum exist.
Warning Errors
IMSL_SOME_CONSTRAINTS_DISCARDED Some constraints were discarded because they were too linearly dependent on other active constraints.
IMSL_ALL_CONSTR_NOT_SATISFIED All constraints are not satisfied. If a feasible solution is possible then try using refinement by supplying optional argument IMSL_REFINEMENT.
IMSL_CYCLING_OCCURRING The algorithm appears to be cycling. Using refinement may help.
Fatal Errors
IMSL_PROB_UNBOUNDED The problem is unbounded.
IMSL_PIVOT_NOT_FOUND An acceptable pivot could not be found.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |