Solves a linear programming problem using the revised simplex algorithm.
NOTE: For double precision, the function lin_prog has generally been superseded by the function linear_programming. Function lin_prog remains in place to ensure compatibility of existing calls.
Synopsis
#include <imsl.h>
float
*imsl_f_lin_prog (int
m, int n, float
a[],
float
b[],
float c[], ¼, 0)
The type double function is imsl_d_lin_prog.
Required Arguments
int m
(Input)
Number of constraints.
int n
(Input)
Number of variables.
float a[]
(Input)
Array of size m ´ n containing a matrix with
coefficients of the m constraints.
float b[]
(Input)
Array with m components
containing the right-hand side of the constraints; if there are limits on both
sides of the constraints, then b contains the lower
limit of the constraints.
float c[]
(Input)
Array with n components
containing the coefficients of the objective function.
Return Value
A pointer to the solution x of the linear programming problem. To release this space, use free. If no solution can be computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsl_f_lin_prog (int
m, int n, float
a[],
float
b[],
float
c[],
IMSL_A_COL_DIM, int
a_col_dim,
IMSL_UPPER_LIMIT, float
bu[],
IMSL_CONSTR_TYPE, int
irtype[],
IMSL_LOWER_BOUND, float
xlb[],
IMSL_UPPER_BOUND, float
xub[],
IMSL_MAX_ITN, int
max_itn,
IMSL_OBJ, float
*obj,
IMSL_RETURN_USER, float
x[],
IMSL_DUAL, float
**y,
IMSL_DUAL_USER, float
y[],
0)
Optional Arguments
IMSL_A_COL_DIM, int a_col_dim
(Input)
The column dimension of a.
Default: a_col_dim = n
IMSL_UPPER_LIMIT, float bu[]
(Input)
Array with m components
containing the upper limit of the constraints that have both the lower and the
upper bounds. If no such constraint exists, then
bu is not needed.
IMSL_CONSTR_TYPE, int irtype[]
(Input)
Array with m components
indicating the types of general constraints in the matrix a. Let ri = ai1x1 + ¼ + ainxn. Then, the value
of irtype(i) signifies the
following:
|
irtype(i) |
Constraint |
|
0 |
ri = bi |
|
1 |
ri £ bui |
|
2 |
ri ³ bi |
|
3 |
bi £ ri £ bui |
Default: irtype = 0
IMSL_LOWER_BOUND, float xlb[]
(Input)
Array with n components
containing the lower bound on the variables. If there is no lower bound on a
variable, then 1030 should be set as the lower
bound.
Default: xlb = 0
IMSL_UPPER_BOUND, float xub[]
(Input)
Array with n components
containing the upper bound on the variables. If there is no upper bound on a
variable, then −1030 should be
set as the upper bound.
Default: xub = ¥
IMSL_MAX_ITN, int max_itn
(Input)
Maximum number of iterations.
Default: max_itn = 10000
IMSL_OBJ, float *obj
(Output)
Optimal value of the objective function.
IMSL_RETURN_USER, float x[]
(Output)
Array with n components
containing the primal solution.
IMSL_DUAL, float **y
(Output)
The address of a pointer y to an array with
m components
containing the dual solution. On return, the necessary space is allocated by
imsl_f_lin_prog.
Typically, float *y is declared, and
&y is used
as an argument.
IMSL_DUAL_USER, float y[]
(Output)
A user-allocated array of size m. On return, y contains the dual
solution.
IMSL_USE_UPDATED_LP_ALGORITHM
(Input)
Calls the function imsl_d_linear_programming
to solve the problem. If this optional argument is present, then the
optional argument IMSL_MAX_ITN is
ignored. This optional argument is only valid in double precision.
Description
The function imsl_f_lin_prog uses a revised simplex method to solve linear programming problems, i.e., problems of the form
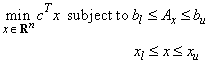
where c is the objective coefficient vector, A is the coefficient matrix, and the vectors bl, bu, xl, and xu are the lower and upper bounds on the constraints and the variables, respectively.
For a complete description of the revised simplex method, see Murtagh (1981) or Murty (1983).
Examples
Example 1
The linear programming problem in the standard form

is solved.
#include
<imsl.h>
main()
{
int m = 4;
int n = 6;
float a[ ] = {1.0, 1.0, 1.0, 0.0, 0.0,
0.0,
1.0, 1.0, 0.0, -1.0, 0.0,
0.0,
1.0, 0.0, 0.0, 0.0, 1.0,
0.0,
0.0, 1.0, 0.0, 0.0, 0.0, 1.0};
float b[ ] = {1.5, 0.5, 1.0,
1.0};
float c[ ] =
{-1.0, -3.0, 0.0, 0.0, 0.0, 0.0};
float
*x;
/* Solve the LP problem */
x = imsl_f_lin_prog
(m, n, a, b, c,
0);
/* Print x */
imsl_f_write_matrix ("x", 1, 6, x,
0);
}
Output
x
1
2
3
4
5
6
0.5
1.0
0.0
1.0
0.5 0.0
Example 2
The linear programming problem in the previous example can be formulated as follows:
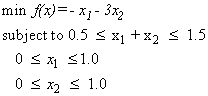
This problem can be solved more efficiently.
#include
<imsl.h>
main()
{
int irtype[ ] =
{3};
int m
= 1;
int n
= 2;
float xub[ ] =
{1.0, 1.0};
float a[
] = {1.0, 1.0};
float b[ ] =
{0.5};
float bu[
] = {1.5};
float
c[ ] = {-1.0, -3.0};
float d[1];
float obj,
*x;
/* Solve the LP problem
*/
x = imsl_f_lin_prog (m, n, a, b,
c,
IMSL_UPPER_LIMIT, bu,
IMSL_CONSTR_TYPE,
irtype,
IMSL_UPPER_BOUND,
xub,
IMSL_DUAL_USER,
d,
IMSL_OBJ,
&obj,
0);
/* Print x */
imsl_f_write_matrix ("x", 1, 2, x,
0);
/* Print d */
imsl_f_write_matrix ("d", 1, 1, d,
0);
printf("\n obj = %g \n", obj);
}
Output
x
1
2
0.5
1.0
d
-1
obj = -3.5
Warning Errors
IMSL_PROB_UNBOUNDED The problem is unbounded.
IMSL_TOO_MANY_ITN Maximum number of iterations exceeded.
IMSL_PROB_INFEASIBLE The problem is infeasible.
Fatal Errors
IMSL_NUMERIC_DIFFICULTY Numerical difficulty occurred (moved to a vertex that is poorly conditioned). If float is currently being used, using double precision may help.
IMSL_BOUNDS_INCONSISTENT The bounds are inconsistent.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |