Solves a real symmetric definite linear system using a conjugate gradient method. Using optional arguments, a preconditioner can be supplied.
Synopsis
#include <imsl.h>
float *imsl_f_lin_sol_def_cg (int n, void amultp ( ), float *b, ..., 0)
The type double function is imsl_d_lin_sol_def_cg.
Required Arguments
int n
(Input)
Number of rows in the matrix.
void amultp
(float
*p,
float
*z)
User-supplied function
which computes z = Ap.
float *b
(Input)
Vector of length n containing the
right-hand side.
Return Value
A pointer to the solution x of the linear system Ax = b. To release this space, use free. If no solution was computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsl_f_lin_sol_def_cg (int n, void amultp(), float
*b,
IMSL_RETURN_USER, float x[],
IMSL_MAX_ITER, int
*maxit,
IMSL_REL_ERR, float relative_error,
IMSL_PRECOND,
void precond(),
IMSL_JACOBI, float
*diagonal,
IMSL_FCN_W_DATA, void amultp(), void
*data,
IMSL_PRECOND_W_DATA, void precond(), void
*data,
0)
Optional Arguments
IMSL_RETURN_USER, float x[]
(Output)
A user-allocated array of length n containing the solution
x.
IMSL_MAX_ITER, int *maxit
(Input/Output)
A pointer to an integer, initially set to the maximum number
of iterations allowed. On exit, the number of iterations used is returned.
IMSL_REL_ERR, float
relative_error (Input)
The relative error
desired.
Default: relative_error =
sqrt(imsl_f_machine(4))
IMSL_PRECOND, void precond
(float
*r,
float
*z) (Input)
User supplied function which sets z =
M -1r,
where M is the preconditioning matrix.
IMSL_JACOBI, float
diagonal[] (Input)
Use the Jacobi preconditioner, i.e.
M = diag(A). The user-supplied vector diagonal should be set
so that diagonal[i] = Aii.
IMSL_FCN_W_DATA, void amultp
(float *p, float *z, void *data),
void
*data, (Input)
User supplied function which computes z =
Ap, which also accepts a pointer to data that is supplied by the
user. data
is a pointer to the data to be passed to the user-supplied function. See
the Introduction, Passing Data to User-Supplied Functions at the
beginning of this manual for more details.
IMSL_PRECOND_W_DATA, void precond
(float
*r,
float
*z, void
*data), void *data,
(Input)
User supplied function which sets z = M -1r, where M is the
preconditioning matrix, which also accepts a pointer to data that is supplied by
the user. data
is a pointer to the data to be passed to the user-supplied function.
See the Introduction, Passing Data to User-Supplied Functions at the
beginning of this manual for more details.
Description
The function imsl_f_lin_sol_def_cg solves the symmetric definite linear system Ax = b using the conjugate gradient method with optional preconditioning. This method is described in detail by Golub and Van Loan (1983, Chapter 10), and in Hageman and Young (1981, Chapter 7).
The preconditioning matrix M is a matrix that approximates A, and for which the linear system Mz = r is easy to solve. These two properties are in conflict; balancing them is a topic of much current research. In the default use of imsl_f_lin_sol_def_cg, M = I. If the option IMSL_JACOBI is selected, M is set to the diagonal of A.
The number of iterations needed depends on the matrix and the error tolerance. As a rough guide,
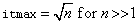
See the references mentioned above for details.
Let M be the preconditioning matrix, let b, p, r, x, and z be vectors and let τ be the desired relative error. Then the algorithm used is as follows:

Here λ is an estimate of λmax(G), the
largest eigenvalue of the iteration matrix
G = I
−M
-1 A. The stopping
criterion is based on the result (Hageman and Young 1981, pp. 148-151)
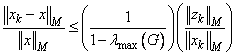
where
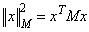
It is also known that
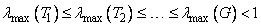
where the Tn are the symmetric, tridiagonal matrices

with μk= 1 − βk/αk-1 − 1/αk, μ1 = 1 − 1/α1 and
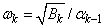
Usually the eigenvalue computation is needed for only a few of the iterations.
Example 1
In this example, the solution to a linear system is found. The coefficient matrix is stored as a full matrix.
#include <imsl.h>
static void amultp (float*, float*);
void main()
{
int n = 3;
float b[] = {27.0, -78.0, 64.0};
float *x;
x =
imsl_f_lin_sol_def_cg (n, amultp, b, 0);
imsl_f_write_matrix ("x", 1, n, x, 0);
}
static void amultp (float *p, float *z)
{
static float a[] = {1.0, -3.0, 2.0,
-3.0, 10.0, -5.0,
2.0, -5.0, 6.0};
int n = 3;
imsl_f_mat_mul_rect ("A*x",
IMSL_A_MATRIX, n, n, a,
IMSL_X_VECTOR, n, p,
IMSL_RETURN_USER, z,
0);
}
Output
x
1 2 3
1 -4 7
Example 2
In this example, two different preconditioners are used to find the solution of a linear system which occurs in a finite difference solution of Laplace’s equation on a regular c × c grid, c = 100. The matrix is A = E (c2, c). For the first solution, select Jacobi preconditioning and supply the diagonal, so M = diag (A). The number of iterations performed and the maximum absolute error are printed. Next, use a more complicated preconditioning matrix, M, consisting of the symmetric tridiagonal part of A.
Notice that the symmetric positive definite band solver is used to factor M once, and subsequently just perform forward and back solves. Again, the number of iterations performed and the maximum absolute error are printed. Note the substantial reduction in iterations.
#include <imsl.h>
static void amultp (float*, float*);
static void precond (float*, float*);
static Imsl_f_sparse_elem *a;
static int n = 2500;
static int c = 50;
static int nz;
void main()
{
int maxit = 1000;
int i;
int index;
float *b;
float *x;
float *mod_five;
float *diagonal;
float norm;
n = c*c;
mod_five = (float*) malloc (n*sizeof(*mod_five));
diagonal = (float*) malloc (n*sizeof(*diagonal));
b = (float*) malloc (n*sizeof(*b));
/* Generate coefficient matrix */
a =
imsl_f_generate_test_coordinate (n, c, &nz, 0);
/* Set a predetermined answer and diagonal */
for (i=0;
i<n; i++) {
mod_five[i] = (float) (i % 5);
diagonal[i] = 4.0;
}
/* Get right hand side */
amultp
(mod_five, b);
/* Solve with jacobi preconditioning */
x =
imsl_f_lin_sol_def_cg (n, amultp, b,
IMSL_MAX_ITER, &maxit,
IMSL_JACOBI, diagonal,
0);
/* Find max absolute error, print results */
norm =
imsl_f_vector_norm (n, x,
IMSL_SECOND_VECTOR, mod_five,
IMSL_INF_NORM, &index,
0);
printf ("iterations = %d, norm = %e\n", maxit, norm);
free (x);
/* Solve same system, with different preconditioner */
x =
imsl_f_lin_sol_def_cg (n, amultp, b,
IMSL_MAX_ITER, &maxit,
IMSL_PRECOND, precond,
0);
norm =
imsl_f_vector_norm (n, x,
IMSL_SECOND_VECTOR, mod_five,
IMSL_INF_NORM, &index,
0);
printf ("iterations = %d, norm = %e\n", maxit, norm);
}
/* Set z = Ap */
static void amultp (float *p, float *z)
{
imsl_f_mat_mul_rect_coordinate ("A*x",
IMSL_A_MATRIX, n, n, nz, a,
IMSL_X_VECTOR, n, p,
IMSL_RETURN_USER_VECTOR, z,
0);
}
/* Solve Mz = r */
static void precond (float *r, float *z)
{
static float *m;
static float *factor;
static int first = 1;
float *null = (float*) 0;
if (first)
{
/* Factor
the first time through */
m = imsl_f_generate_test_band (n, 1,
IMSL_SYMMETRIC_STORAGE, 0);
imsl_f_lin_sol_posdef_band (n, m, 1, null,
IMSL_FACTOR, &factor,
IMSL_FACTOR_ONLY,
0);
first = 1;
}
/* Perform the forward and back solves */
imsl_f_lin_sol_posdef_band (n, m, 1, r,
IMSL_FACTOR_USER, factor,
IMSL_SOLVE_ONLY,
IMSL_RETURN_USER, z,
0);
}
Output
iterations = 115, norm = 1.382828e-05
iterations = 75, norm = 7.319450e-05
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |