Solves a linear system Ax = b using the restarted generalized minimum residual (GMRES) method.
Synopsis
#include <imsl.h>
float *imsl_f_lin_sol_gen_min_residual (int n, void amultp (float *p, float *z), float *b, ..., 0)
The type double function is imsl_d_lin_sol_gen_min_residual.
Required Arguments
int n
(Input)
Number of rows in the matrix.
void amultp
(float *p, float *z)
User-supplied function which computes
z = Ap.
float *b
(Input)
Vector of length n containing the
right-hand side.
Return Value
A pointer to the solution x of the linear system Ax = b. To release this space, use free. If no solution was computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsl_f_lin_sol_gen_min_residual (int n, void amultp (),
float *b,
IMSL_RETURN_USER, float x[],
IMSL_MAX_ITER,
int *maxit,
IMSL_REL_ERR, float tolerance,
IMSL_PRECOND,
void precond(),
IMSL_MAX_KRYLOV_SUBSPACE_DIM, int
kdmax,
IMSL_HOUSEHOLDER_REORTHOG,
IMSL_FCN_W_DATA, void amultp
(), void *data,
IMSL_PRECOND_W_DATA, void
precond(), void *data,
0)
Optional Arguments
IMSL_RETURN_USER, float x[]
(Output)
A user-allocated array of length n containing the
solution x.
IMSL_MAX_ITER, int *maxit
(Input/Output)
A pointer to an integer, initially set to the maximum number
of GMRES iterations allowed. On exit, the number of iterations used is
returned.
Default: maxit = 1000
IMSL_REL_ERR, float tolerance
(Input)
The algorithm attempts to generate x such that ||b −
Ax||2 £ τ||b||2, where
τ = tolerance.
Default:
tolerance =
sqrt(imsl_f_machine(4))
IMSL_PRECOND, void precond
(float
*r,
float
*z) (Input)
User supplied function which sets z =
M -1r,
where M is the preconditioning matrix.
IMSL_MAX_KRYLOV_SUBSPACE_DIM, int kdmax,
(Input)
The maximum Krylov subspace dimension, i.e., the maximum allowable
number of GMRES iterations allowed before restarting.
Default: kdmax = imsl_i_min(n, 20)
IMSL_HOUSEHOLDER_REORTHOG,
Perform
orthogonalization by Householder transformations, replacing the Gram-Schmidt
process.
IMSL_FCN_W_DATA, void amultp
(float *p, float *z, void *data),
void *data,
(Input)
User supplied function which computes z = Ap, which
also accepts a pointer to data that is supplied by the user. data is a pointer to
the data to be passed to the user-supplied function. See the
Introduction, Passing Data to User-Supplied Functions at the beginning of
this manual for more details.
IMSL_PRECOND_W_DATA, void precond
(float
*r,
float
*z, void
*data), void *data
(Input)
User supplied function which sets z = M -1r, where M is the
preconditioning matrix, which also accepts a pointer to data that is supplied by
the user. data is a pointer to
the data to be passed to the user-supplied function. See the
Introduction, Passing Data to User-Supplied Functions at the beginning of
this manual for more details.
Description
The function imsl_f_lin_sol_gen_min_residual, based on the FORTRAN subroutine GMRES by H.F. Walker, solves the linear system Ax = b using the GMRES method. This method is described in detail by Saad and Schultz (1986) and Walker (1988).
The GMRES method begins with an approximate solution
x0 and an initial
residual
r0 = b −
Ax0. At iteration
m, a correction zm is determined in the
Krylov subspace
κm (v) = span (v, Av, …, Am-1v)
v = r0 which solves the least-squares problem
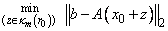
Then at iteration m, xm = x0 + zm.
Orthogonalization by Householder transformations requires less storage but more arithmetic than Gram-Schmidt. However, Walker (1988) reports numerical experiments which suggest the Householder approach is more stable, especially as the limits of residual reduction are reached.
Examples
Example 1
As an example, consider the following matrix:

Let xT = (1, 2, 3, 4, 5, 6) so that Ax = (10, 7, 45, 33, −34, 31)T. The function imsl_f_mat_mul_rect_coordinate is used to form the product Ax.
#include <imsl.h>
void amultp (float*, float*);
main()
{
float b[] = {10.0, 7.0, 45.0, 33.0, -34.0, 31.0};
int n = 6;
float *x;
x =
imsl_f_lin_sol_gen_min_residual (n, amultp, b,
0);
imsl_f_write_matrix ("Solution, x, to Ax = b", 1, n, x, 0);
}
void amultp (float *p, float *z)
{
Imsl_f_sparse_elem a[] = {0, 0, 10.0,
1, 1, 10.0,
1, 2, -3.0,
1, 3, -1.0,
2, 2, 15.0,
3, 0, -2.0,
3, 3, 10.0,
3, 4, -1.0,
4, 0, -1.0,
4, 3, -5.0,
4, 4, 1.0,
4, 5, -3.0,
5, 0, -1.0,
5, 1, -2.0,
5, 5, 6.0};
int n = 6;
int nz = 15;
imsl_f_mat_mul_rect_coordinate ("A*x",
IMSL_A_MATRIX, n, n, nz, a,
IMSL_X_VECTOR, n, p,
IMSL_RETURN_USER_VECTOR, z,
0);
}
Output
Solution, x, to Ax = b
1 2 3 4 5 6
1 2 3 4 5 6
Example 2
In this example, the same system given in the first example is solved. This time a preconditioner is provided. The preconditioned matrix is chosen as the diagonal of A.
#include <imsl.h>
void amultp (float*, float*);
void precond (float*, float*);
main()
{
float b[] = {10.0, 7.0, 45.0, 33.0, -34.0, 31.0};
int n = 6;
float *x;
int maxit = 1000;
x =
imsl_f_lin_sol_gen_min_residual (n, amultp, b,
IMSL_MAX_ITER, &maxit,
IMSL_PRECOND, precond,
0);
imsl_f_write_matrix ("Solution, x, to Ax = b", 1, n, x, 0);
printf ("\nNumber of iterations taken = %d\n", maxit);
}
/* Set z = Ap */
void amultp (float *p, float *z)
{
static Imsl_f_sparse_elem a[] = {0, 0, 10.0,
1, 1, 10.0,
1, 2, -3.0,
1, 3, -1.0,
2, 2, 15.0,
3, 0, -2.0,
3, 3, 10.0,
3, 4, -1.0,
4, 0, -1.0,
4, 3, -5.0,
4, 4, 1.0,
4, 5, -3.0,
5, 0, -1.0,
5, 1, -2.0,
5, 5, 6.0};
int n = 6;
int nz = 15;
imsl_f_mat_mul_rect_coordinate ("A*x",
IMSL_A_MATRIX, n, n, nz, a,
IMSL_X_VECTOR, n, p,
IMSL_RETURN_USER_VECTOR, z,
0);
}
/* Solve Mz = r */
void precond (float *r, float *z)
{
static float diagonal_inverse[] =
{0.1, 0.1, 1.0/15.0, 0.1, 1.0, 1.0/6.0};
int n = 6;
int i;
for (i=0;
i<n; i++)
z[i] = diagonal_inverse[i]*r[i];
}
Output
Solution, x, to Ax = b
1 2 3 4 5 6
1 2 3 4 5 6
Number of iterations taken = 5
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |