Fits a multiple linear regression model using least squares.
Synopsis
#include <imsl.h>
float
*imsl_f_regression (int
n_observations, int
n_independent,
float
x[],
float
y[], ¼, 0)
The type double function is imsl_d_regression.
Required Arguments
int
n_observations (Input)
The number of observations.
int
n_independent (Input)
The number of independent
(explanatory) variables.
float x[]
(Input)
Array of size n_observations ´ n_independent
containing the matrix of independent (explanatory) variables.
float y[]
(Input)
Array of length n_observations
containing the dependent (response) variable.
Return Value
If the optional argument IMSL_NO_INTERCEPT is not used, imsl_f_regression returns a pointer to an array of length n_independent + 1 containing a least-squares solution for the regression coefficients. The estimated intercept is the initial component of the array.
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsl_f_regression (int
n_observations, int
n_independent,
float
x[],
float
y[],
IMSL_X_COL_DIM, int
x_col_dim,
IMSL_NO_INTERCEPT,
IMSL_TOLERANCE, float
tolerance,
IMSL_RANK, int
*rank,
IMSL_COEF_COVARIANCES, float
**p_coef_covariances,
IMSL_COEF_COVARIANCES_USER, float
coef_covariances[],
IMSL_COV_COL_DIM, int
cov_col_dim,
IMSL_X_MEAN, float
**p_x_mean,
IMSL_X_MEAN_USER, float
x_mean[],
IMSL_RESIDUAL, float
**p_residual,
IMSL_RESIDUAL_USER, float
residual[],
IMSL_ANOVA_TABLE, float
**p_anova_table,
IMSL_ANOVA_TABLE_USER, float
anova_table[],
IMSL_RETURN_USER, float
coefficients[],
0)
Optional Arguments
IMSL_X_COL_DIM, int x_col_dim
(Input)
The column dimension of x.
Default: x_col_dim = n_independent
IMSL_NO_INTERCEPT
By
default, the fitted value for observation i is
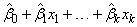
where k = n_independent. If IMSL_NO_INTERCEPT is specified, the intercept term
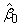
is omitted from the model.
IMSL_TOLERANCE, float tolerance
(Input)
The tolerance used in determining linear dependence. For imsl_f_regression,
tolerance = 100 ´ imsl_f_machine(4) is
the default choice. For imsl_d_regression,
tolerance = 100 ´ imsl_d_machine(4) is
the default. See imsl_f_machine
(page .p<.CMCH12.DOC!MACHINE_FLOAT;635;).
IMSL_RANK, int *rank
(Output)
The rank of the fitted model is returned in *rank.
IMSL_COEF_COVARIANCES, float
**p_coef_covariances (Output)
The address of a pointer to
the m ´ m array
containing the estimated variances and covariances of the estimated regression
coefficients. Here, m is the number of regression coefficients in the
model. If IMSL_NO_INTERCEPT is
specified, m = n_independent;
otherwise, m = n_independent + 1.
On return, the pointer is initialized (through a memory allocation request to
malloc), and the
array is stored there. Typically, float *p_coef_covariances is
declared; &p_coef_covariances
is used as an argument to this function; and free(p_coef_covariances) is
used to free this array.
IMSL_COEF_COVARIANCES_USER, float
coef_covariances[] (Output)
If specified, coef_covariances is an
array of length m ´ m containing the estimated
variances and covariances of the estimated coefficients where m is the
number of regression coefficients in the model.
IMSL_COV_COL_DIM, int
cov_col_dim (Input)
The column dimension of array coef_covariance.
Default:
cov_col_dim = m
where m is the number of regression coefficients in the model.
IMSL_X_MEAN, float
**p_x_mean (Output)
The address of a pointer to the array
containing the estimated means of the independent variables. On return, the
pointer is initialized (through a memory allocation request to malloc), and the array
is stored there. Typically, float *p_x_mean is declared;
&p_x_mean is
used as an argument to this function; and free(p_x_mean) is used to
free this array.
IMSL_X_MEAN_USER, float x_mean[]
(Output)
If specified, x_mean is an array of
length n_independent provided
by the user. On return, x_mean contains the
means of the independent variables.
IMSL_RESIDUAL, float
**p_residual (Output)
The address of a pointer to the
array containing the residuals. On return, the pointer is initialized (through a
memory allocation request to malloc), and the array
is stored there. Typically, float *p_residual is
declared; &p_residual is
used as argument to this function; and free(p_residual) is used to
free this array.
IMSL_RESIDUAL_USER, float
residual[] (Output)
If specified, residual is an array
of length n_observations
provided by the user. On return, residual contains the
residuals.
IMSL_ANOVA_TABLE, float
**p_anova_table (Output)
The address of a pointer to the
array containing the analysis of variance table. On return, the pointer is
initialized (through a memory allocation request to malloc), and the array
is stored there. Typically, float *p_anova_table is
declared; &p_anova_table is
used as argument to this function; and free(p_anova_table) is used
to free this array.
The analysis of variance statistics are given as follows:
|
Element |
Analysis of Variance Statistics |
|
0 |
degrees of freedom for the model |
|
1 |
degrees of freedom for error |
|
2 |
total (corrected) degrees of freedom |
|
3 |
sum of squares for the model |
|
4 |
sum of squares for error |
|
5 |
total (corrected) sum of squares |
|
6 |
model mean square |
|
7 |
error mean square |
|
8 |
overall F-statistic |
|
9 |
p-value |
|
10 |
R2 (in percent) |
|
11 |
adjusted R2 (in percent) |
|
12 |
estimate of the standard deviation |
|
13 |
overall mean of y |
|
14 |
coefficient of variation (in percent) |
IMSL_ANOVA_TABLE_USER, float
anova_table[] (Output)
If specified, the 15 analysis of
variance statistics listed above are computed and stored in the array anova_table provided
by the user.
IMSL_RETURN_USER, float
coefficients[] (Output)
If specified, the least-squares
solution for the regression coefficients is stored in array coefficients provided
by the user. If IMSL_NO_INTERCEPT is
specified, the array requires m = n_independent units of
memory; otherwise, the number of units of memory required to store the
coefficients is m = n_independent + 1.
Description
The function imsl_f_regression fits a multiple linear regression model with or without an intercept. By default, the multiple linear regression model is
yi = b0 + b1xi1 +b2xi2 + ¼ + bkxik + ei i = 1, 2, ¼, n
where the observed values of the yi’s (input in y) are the responses or values of the dependent variable; the xi1’s, xi2’s, ¼, xik’s (input in x) are the settings of the k (input in n_independent) independent variables; β0, β1, ¼, βk are the regression coefficients whose estimated values are to be output by imsl_f_regression; and the ɛi’s are independently distributed normal errors each with mean zero and variance σ2. Here, n is the number of rows in the augmented matrix (x,y), i.e., n equals n_observations. Note that by default, β0 is included in the model.
The function imsl_f_regression computes estimates of the regression coefficients by minimizing the sum of squares of the deviations of the observed response yi from the fitted response
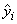
for the n observations. This minimum sum of squares (the error sum of squares) is output as one of the analysis of variance statistics if IMSL_ANOVA_TABLE (or IMSL_ANOVA_TABLE_USER) is specified and is computed as
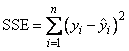
Another analysis of variance statistic is the total sum of squares. By default, the total sum of squares is the sum of squares of the deviations of yi from its mean
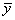
the so-called corrected total sum of squares. This statistic is computed as
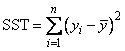
When IMSL_NO_INTERCEPT is specified, the total sum of squares is the sum of squares of yi, the so-called uncorrected total sum of squares. This is computed as
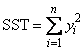
See Draper and Smith (1981) for a good general treatment of the multiple linear regression model, its analysis, and many examples.
In order to compute a least-squares solution, imsl_f_regression performs an orthogonal reduction of the matrix of regressors to upper-triangular form. The reduction is based on one pass through the rows of the augmented matrix (x, y) using fast Givens transformations. (See Golub and Van Loan 1983, pp. 156−162; Gentleman 1974.) This method has the advantage that the loss of accuracy resulting from forming the crossproduct matrix used in the normal equations is avoided.
By default, the current means of the dependent and
independent variables are used to internally center the data for improved
accuracy. Let xi be a column vector
containing the j-th row of data for the independent variables. Let
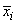represent the mean
vector for the independent variables given the data for rows 1, 2, ¼, i. The current mean vector is
defined to be
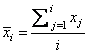
The i-th row of data has 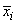subtracted from it and is
then weighted by i/(i − 1). Although a
crossproduct matrix is not computed, the validity of this centering operation
can be seen from the following formula for the sum of squares and crossproducts
matrix:
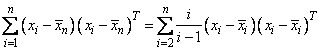
An orthogonal reduction on the centered matrix is computed. When the final computations are performed, the intercept estimate and the first row and column of the estimated covariance matrix of the estimated coefficients are updated (if IMSL_COEF_COVARIANCES or IMSL_COEF_COVARIANCES_USER is specified) to reflect the statistics for the original (uncentered) data. This means that the estimate of the intercept is for the uncentered data.
As part of the final computations, imsl_regression checks for linearly dependent regressors. In particular, linear dependence of the regressors is declared if any of the following three conditions are satisfied:
• A regressor equals zero.
• Two or more regressors are constant.
•
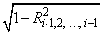is less than or equal
to tolerance.
Here, Ri.1,2, ¼, i-1 is the
multiple correlation coefficient of the i-th independent variable with
the first
i − 1 independent
variables. If no intercept is in the model, the “multiple correlation”
coefficient is computed without adjusting for the mean.
On completion of the final computations, if the i-th regressor is declared to be linearly dependent upon the previous i − 1 regressors, then the i-th coefficient estimate and all elements in the i-th row and i-th column of the estimated variance-covariance matrix of the estimated coefficients (if IMSL_COEF_COVARIANCES or IMSL_COEF_COVARIANCES_USER is specified) are set to zero. Finally, if a linear dependence is declared, an informational (error) message, code IMSL_RANK_DEFICIENT, is issued indicating the model is not full rank.
Examples
Example 1
A regression model
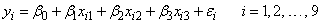
is fitted to data taken from Maindonald (1984, pp. 203−204).
#include
<imsl.h>
#define INTERCEPT
1
#define N_INDEPENDENT 3
#define N_COEFFICIENTS
(INTERCEPT + N_INDEPENDENT)
#define N_OBSERVATIONS
9
main()
{
float *coefficients;
float x[][N_INDEPENDENT] = {7.0, 5.0,
6.0,
2.0,-1.0,
6.0,
7.0, 3.0,
5.0,
-3.0, 1.0,
4.0,
2.0,-1.0,
0.0,
2.0, 1.0,
7.0,
-3.0,-1.0,
3.0,
2.0, 1.0,
1.0,
2.0, 1.0, 4.0};
float
y[] = {7.0,-5.0, 6.0, 5.0, 5.0, -2.0, 0.0, 8.0, 3.0};
coefficients = imsl_f_regression(N_OBSERVATIONS, N_INDEPENDENT,
(float *)x, y, 0);
imsl_f_write_matrix("Least-Squares
Coefficients", 1, N_COEFFICIENTS,
coefficients,
IMSL_COL_NUMBER_ZERO,
0);
}
Output
Least-Squares
Coefficients
0
1
2
3
7.733
-0.200 2.333
-1.667
Example 2
A weighted least-squares fit is computed using the model
yi = b0xi0 +b1xi1 + b2xi2 + ei i = 1, 2, ¼, 4
and weights 1/i2 discussed by Maindonald (1984, pp. 67−68). In order to compute the weighted least-squares fit, using an ordinary least-squares function (imsl_f_regression), the regressors (including the column of ones for the intercept term) and the responses must be transformed prior to invocation of imsl_f_regression. Specifically, the i-th response and regressors are multiplied by a square root of the i-th weight. IMSL_NO_INTERCEPT must be specified since the column of ones corresponding to the intercept term in the untransformed model is transformed by the weights and is regarded as an additional independent variable.
In the example, IMSL_ANOVA_TABLE is specified. The minimum sum of squares for error in terms of the original untransformed regressors and responses for this weighted regression is
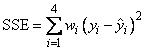
where wi = 1/i2. Also, since IMSL_NO_INTERCEPT is specified, the uncorrected total sum-of-squares terms of the original untransformed responses is
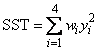
#include
<imsl.h>
#include <math.h>
#define
N_INDEPENDENT 3
#define N_COEFFICIENTS
N_INDEPENDENT
#define N_OBSERVATIONS
4
main()
{
int i, j;
float *coefficients, w, anova_table[15],
power;
float
x[][N_INDEPENDENT] = {1.0, -2.0, 0.0,
1.0, -1.0, 2.0,
1.0, 2.0,
5.0,
1.0, 7.0, 3.0};
float y[] = {-3.0, 1.0, 2.0,
6.0};
char
*anova_row_labels[] =
{
"degrees of freedom for regression",
"degrees of freedom for error",
"total (uncorrected) degrees of
freedom",
"sum of squares for regression",
"sum of squares for error",
"total (uncorrected) sum of
squares",
"regression mean square",
"error mean square",
"F-statistic",
"p-value", "R-squared (in percent)",
"adjusted
R-squared (in
percent)",
"est. standard deviation of model error",
"overall mean of y",
"coefficient of variation (in percent)"};
power =
0.0;
for (i = 0; i < N_OBSERVATIONS;
i++) {
power +=
1.0;
/* The square root of the weight
*/
w = sqrt(1.0 /
(power*power));
/* Transform response */
y[i] *=
w;
/* Transform regressors */
for (j
= 0; j < N_INDEPENDENT;
j++)
x[i][j] *= w;
}
coefficients =
imsl_f_regression(N_OBSERVATIONS, N_INDEPENDENT,
(float *)x,
y,
IMSL_NO_INTERCEPT,
IMSL_ANOVA_TABLE_USER,
anova_table, 0);
imsl_f_write_matrix("Least-Squares
Coefficients",
1,
N_COEFFICIENTS, coefficients, 0);
imsl_f_write_matrix("* *
* Analysis of Variance * * *\n", 15, 1,
anova_table, IMSL_ROW_LABELS,
anova_row_labels,
IMSL_WRITE_FORMAT, "%10.2f", 0);
}
Output
Least-Squares Coefficients
1 2
3
-1.431
0.658
0.748
* * *
Analysis of Variance * * *
degrees of freedom for
regression
3.00
degrees of freedom for
error
1.00
total (uncorrected) degrees of
freedom 4.00
sum of squares for
regression
10.93
sum of squares for
error
1.01
total (uncorrected) sum of
squares
11.94
regression mean
square
3.64
error mean
square
1.01
F-statistic
3.60
p-value
0.37
R-squared (in
percent)
91.52
adjusted R-squared (in
percent)
66.08
est. standard deviation of model
error 1.01
overall mean of y
-0.08
coefficient
of variation (in percent) -1207.73
Warning Errors
IMSL_RANK_DEFICIENT The model is not full rank. There is not a unique least-squares solution.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |