Computes a least-squares spline approximation.

Synopsis

#include <imsl.h>

Imsl_f_spline *imsl_f_spline_least_squares (int ndata, float xdata[], float fdata[], int spline_space_dim, ¼, 0)

The type Imsl_d_spline function is imsl_d_spline_least_squares.

Required Arguments

int ndata   (Input)
Number of data points.

float xdata[]   (Input)
Array with ndata components containing the abscissas of the least-squares problem.

float fdata[]   (Input)
Array with ndata components containing the ordinates of the least-squares problem.

int spline_space_dim   (Input)
The linear dimension of the spline subspace. It should be smaller than ndata and greater than or equal to order (whose default value is 4).

Return Value

A pointer to the structure that represents the spline fit. If a fit cannot be computed, then NULL is returned. To release this space, use free.

Synopsis with Optional Arguments

#include <imsl.h>

Imsl_f_spline *imsl_f_spline_least_squares (int ndata, float xdata[], float fdata[], int spline_space_dim,
IMSL_SSE, float *sse_err,
IMSL_WEIGHTS, float weights[],
IMSL_ORDER, int order,
IMSL_KNOTS, float knots[],
IMSL_OPTIMIZE,
0)

Optional Arguments

IMSL_SSE, float *sse   (Output)
This option places the weighted error sum of squares in the place pointed to by sse.

IMSL_WEIGHTS, float weights[]   (Input)
This option requires the user to provide the weights.
Default: all weights equal one.

IMSL_ORDER, int order   (Input)
The order of the spline subspace for which the knots are desired. This option is used to communicate the order of the spline subspace.
Default: order = 4, (i.e., cubic splines).

IMSL_KNOTS, float knots[]   (Input)
This option requires the user to provide the knots. The user must provide a knot sequence of length spline_space_dimension + order.
Default: an appropriate knot sequence is selected. See below for more details.

IMSL_OPTIMIZE
This option optimizes the knot locations, by attempting to minimize the least-squares error as a function of the knots. The optimal knots are available in the returned spline structure.

Description

Let’s make the identifications

n = ndata

x = xdata

f = fdata

m = spline_space_dim

k = order

For convenience, we assume that the sequence x is increasing, although the function does not require this.

By default, k = 4, and the knot sequence we select equally distributes the knots through the distinct xi’s. In particular, the m + k knots will be generated in [x1, xn] with k knots stacked at each of the extreme values. The interior knots will be equally spaced in the interval.

Once knots t and weights w are determined (and assuming that the option IMSL_OPTIMIZE is not chosen), then the function computes the spline least-squares fit to the data by minimizing over the linear coefficients aj

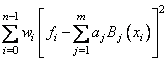
where the Bj, j = 1, ¼, m are a (B-spline) basis for the spline subspace.

The optional argument IMSL_ORDER allows the user to choose the order of the spline fit. The optional argument IMSL_KNOTS allows user specification of knots. The function imsl_f_spline_least_squares is based on the routine L2APPR by de Boor (1978, p. 255).

If the option IMSL_OPTIMIZE is chosen, then the procedure attempts to find the best placement of knots that will minimize the least-squares error to the given data by a spline of order k with m coefficients. For this problem to make sense, it is necessary that m > k. We then attempt to find the minimum of the functional

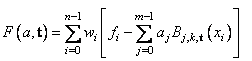
The technique employed here uses the fact that for a fixed knot sequence t the minimization in a is a linear least-squares problem that can be easily solved. Thus, we can think of our objective function F as a function of just t by setting

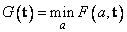
A Gauss-Seidel (cyclic coordinate) method is then used to reduce the value of the new objective function G. In addition to this local method, there is a global heuristic built into the algorithm that will be useful if the data arise from a smooth function. This heuristic is based on the routine NEWNOT of de Boor (1978, pp. 184 and 258−261).

The initial guess, tg, for the knot sequence is either provided by the user or is the default. This guess must be a valid knot sequence for splines of order k with

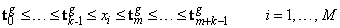
with tg nondecreasing, and

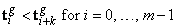
In regard to execution speed, this function can be several orders of magnitude slower than a simple least-squares fit.

The return value for this function is a pointer of type Imsl_f_spline. The calling program must receive this in a pointer Imsl_f_spline *sp. This structure contains all the information to determine the spline (stored in B-spline form) that is computed by this function. For example, the following code sequence evaluates this spline a x and returns the value in y.

y = imsl_f_spline_value (x, sp, 0);

In the figure below two cubic splines are fit to

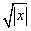
Both splines are cubics with the same spline_space_dim = 8. The first spline is computed with the default settings, while the second spline is computed by optimizing the knot locations using the keyword IMSL_OPTIMIZE.

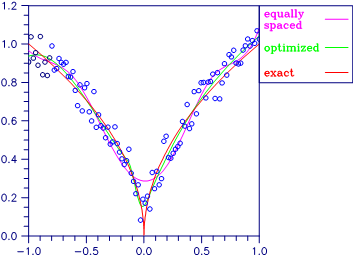
Figure 3- 4   Two Fits to Noisy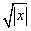

Examples

Example 1

This example fits data generated from a trigonometric polynomial

1 + sinx + 7 sin3x + e

where ɛ is a random uniform deviate over the range [-1, 1]. The data are obtained by evaluating this function at 90 equally spaced points on the interval [0, 6]. This data is fitted with a cubic spline with 12 degrees of freedom (eight equally spaced interior knots). The error at 10 equally spaced points is printed out.

#include <imsl.h>
#include <stdio.h>
#include <math.h>

#define NDATA   90
                                /* Define function */
#define F(x)    (float)(1.+ sin(x)+7.*sin(3.0*x))

main()
{
    int                 i, spline_space_dim = 12;
    float               fdata[NDATA], xdata[NDATA], *random;
    Imsl_f_spline       *sp;
                                /* Generate random numbers */
    imsl_random_seed_set(123457);
    random = imsl_f_random_uniform(NDATA, 0);
                                /* Set up data */
    for (i = 0;  i < NDATA;  i++) {
        xdata[i] = 6.*(float)i /((float)(NDATA-1));
        fdata[i] = F(xdata[i]) + 2.*(random[i]-.5);
    }
    sp = imsl_f_spline_least_squares(NDATA, xdata, fdata,
                                         spline_space_dim, 0);
    printf("       x         error  \n");
    for(i = 0;  i < 10;  i++) {
        float x, error;
        x = 6.*i/9.;
        error = F(x) - imsl_f_spline_value(x, sp, 0);
        printf("%10.3f  %10.3f\n", x, error);
    }
}

Output

   x        Error 
0.000      -0.356
0.667      -0.004
1.333       0.434
2.000      -0.069
2.667      -0.494
3.333       0.362
4.000      -0.273
4.667      -0.247
5.333       0.303
6.000       0.578

Example 2

This example continues with the first example in which we fit data generated from the trigonometric polynomial

1 + sinx + 7 sin3x + e

where ɛ is random uniform deviate over the range [−1, 1]. The data is obtained by evaluating this function at 90 equally spaced points on the interval [0, 6]. This data was fitted with a cubic spline with 12 degrees of freedom (in this case, the default gives us eight equally spaced interior knots) and the error sum of squares was printed. In this example, the knot locations are optimized and the error sum of squares is printed. Then, the error at 10 equally spaced points is printed.

#include <imsl.h>
#include <stdio.h>
#include <math.h>

#define NDATA   90
                                /* Define function */
#define F(x)        (float)(1.+ sin(x)+7.*sin(3.0*x))

main()
{
    int                 i, spline_space_dim = 12;
    float               fdata[NDATA], xdata[NDATA], *random, sse1, sse2;
    Imsl_f_spline        *sp;
                                /* Generate random numbers */
    imsl_random_seed_set(123457);
    random = imsl_f_random_uniform(NDATA, 0);
                                /* Set up data */
    for (i = 0; i < NDATA; i++) {
        xdata[i] = 6.*(float)i /((float)(NDATA-1));
        fdata[i] = F(xdata[i]) + 2.*(random[i]-.5);
    }
    sp = imsl_f_spline_least_squares(NDATA, xdata, fdata,
                                                       spline_space_dim,
                                     IMSL_SSE, &sse1,
                                     0);
    sp = imsl_f_spline_least_squares(NDATA, xdata, fdata,
                                                      spline_space_dim,
                                     IMSL_OPTIMIZE,
                                     IMSL_SSE, &sse2,
                                     0);
    printf("The error sum of squares before optimizing is %10.1f\n",
           sse1);
    printf("The error sum of squares  after optimizing is %10.1f\n\n",            sse2);
    printf("       x         error\n");
    for(i = 0; i < 10;  i++){
        float   x, error;
        x = 6.*i/9.;
        error = F(x) - imsl_f_spline_value(x, sp, 0);
        printf("%10.3f  %10.3f\n", x, error);
    }
}

Output

The error sum of squares before optimizing is       32.6
The error sum of squares  after optimizing is       27.0

       x         Error
     0.000      -0.656
     0.667       0.107
     1.333       0.055
     2.000      -0.243
     2.667      -0.063
     3.333      -0.015
     4.000      -0.424
     4.667      -0.138
     5.333       0.133
     6.000       0.494

Warning Errors

IMSL_OPT_KNOTS_STACKED_1                The knots found to be optimal are stacked more than order. This indicates fewer knots will produce the same error sum of squares. The knots have been separated slightly.

Fatal Errors

IMSL_XDATA_TOO_LARGE                         The array xdata must satisfy xdatai ≤ tndata, for i = 1, ¼, ndata.

IMSL_XDATA_TOO_SMALL                         The array xdata must satisfy
 xdatai ³ torder-1, for i = 1, ¼, ndata.

IMSL_NEGATIVE_WEIGHTS                       All weights must be greater than or equal to zero.

IMSL_KNOT_MULTIPLICITY                     Multiplicity of the knots cannot exceed the order of the spline.

IMSL_KNOT_NOT_INCREASING                The knots must be nondecreasing.

IMSL_OPT_KNOTS_STACKED_2                The knots found to be optimal are stacked more than order. This indicates fewer knots will produce the same error sum of squares.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260