Finds the real zeros of a real function using Müller’s method.

Synopsis

#include <imsl.h>

float *imsl_f_zeros_fcn (float fcn(), ¼, 0)

The type double function is imsl_d_zeros_fcn.

Required Arguments

float fcn (float x)   (Input/Output)
User-supplied function to compute the value of the function of which the zeros will be found, where x is the point at which the function is evaluated.

Return Value

A pointer to the zeros x of the function. To release this space, use free. If no zeros can be found, then NULL is returned.

Synopsis with Optional Arguments

#include <imsl.h>

float *imsl_f_zeros_fcn (float fcn(),
IMSL_XGUESS, float xguess[],
IMSL_NUM_ROOTS, int nroot,
IMSL_ERR_ABS, float err_abs,
IMSL_ERR_REL, float err_rel,
IMSL_ETA, float eta,
IMSL_EPS, float eps,
IMSL_MAX_ITN, int max_itn,
IMSL_RETURN_USER, float x[],
IMSL_INFO, int **info,
IMSL_INFO_USER, int info[],
IMSL_FCN_W_DATA, float fcn ( ), void *data,
0)

Optional Arguments

IMSL_XGUESS, float xguess[]   (Input)
Array with nroot components containing the initial guesses for the zeros.
Default: xguess = 0

IMSL_NUM_ROOTS, int nroot   (Input)
The number of zeros to be found by imsl_f_zeros_fcn.
Default: nroot = 1

IMSL_ERR_ABS, float err_abs   (Input)
First stopping criterion. A zero xi is accepted if |f(xi)| < err_abs.
Default:

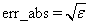
where e is the machine precision

IMSL_ERR_REL, float err_rel   (Input)
Second stopping criterion. A zero xi is accepted if the relative change of two successive approximations to xi is less than err_rel.
Default:

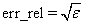
where ɛ is the machine precision

IMSL_ETA, float eta   (Input)
Spread criteria for multiple zeros. If the zero xi has been computed and
|xi − xj| < eps, where xj is a previously computed zero, then the computation is restarted with a guess equal to xi + eta.
Default: eta = 0.01

IMSL_EPS, float eps   (Input)
See eta.
Default:

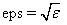
where ɛ is the machine precision

IMSL_MAX_ITN, int max_itn   (Input)
The maximum allowable number of iterations per zero.
Default: max_itn = 100

IMSL_RETURN_USER, float x[]   (Output)
Array with nroot components containing the computed zeros.

IMSL_INFO, int **info   (Output)
The address of a pointer info to an array of length nroot containing convergence information. On return, the necessary space is allocated by imsl_f_zeros_fcn. The value info[j − 1] is the number of iterations used in finding the j-th zero when convergence is achieved. If convergence is not obtained in max_itn iterations, info[j − 1] would be greater than max_itn.

IMSL_INFO_USER, int info[]   (Output)
A user-allocated array with nroot components. On return, the value
info[j − 1] is the number of iterations used in finding the j-th zero when convergence is achieved. If convergence is not obtained in max_itn iterations, info[j − 1] would be greater than max_itn.

IMSL_FCN_W_DATA, float fcn (float x, void *data) , void *data (Input)
User supplied function to compute the value of the function of which the zeros will be found, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.   See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

Description

The function imsl_f_zeros_fcn computes n real zeros of a real function f. Given a user-supplied function f(x) and an n-vector of initial guesses x1, x2, ¼, xn, the function uses Müller’s method to locate n real zeros of f. The function has two convergence criteria: the first requires that

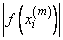
be less than err_abs; the second requires that the relative change of any two successive approximations to an xi be less than err_rel. Here,

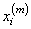
is the m-th approximation to xi. Let err_abs be denoted by ɛ1 and err_rel be denoted by ɛ2. The criteria may be stated mathematically as follows:

Criterion 1:

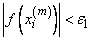
Criterion 2:

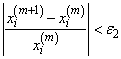
“Convergence” is the satisfaction of either criterion.

Examples

Example 1

This example finds a real zero of the third-degree polynomial

f(x) = x3 − 3x2 + 3x − 1

#include <imsl.h>

float           fcn(float x);

main()
{
    float       *x;
                                /* Solve fcn(x)=0  for  x  */
    x = imsl_f_zeros_fcn (fcn, 0);
                                /* Print x */
    imsl_f_write_matrix ("x", 1, 1, x, 0);
}

float fcn(float x)
{
    return  x * x * x - 3.0 * x * x + 3.0 * x - 1.0;
}

Output

     x
         1

 

Example 2

This example finds three real zeros of the third-degree polynomial

f(x) = x3 + 3x2 − 4x − 6

with the three initial guesses (4.6, 0.0, −193.3).

#include <imsl.h>

float           fcn(float x);

main()
{
    float       xguess[ ] =  {4.6, 0.0, -193.3};
    int         nroot = 3;
    float       eps = 1.0e-5;
    float       err_abs = 1.0e-5;
    float       err_rel = 1.0e-5;
    float       eta = 1.0e-2;
    int         max_itn = 100;
    float       *x;
                                /* Solve fcn(x)=0  for  x  */
    x = imsl_f_zeros_fcn (fcn,
                          IMSL_XGUESS, xguess,
                          IMSL_ERR_REL, err_rel,
                          IMSL_ERR_ABS, err_abs,
                          IMSL_ETA, eta,
                          IMSL_EPS, eps,
                          IMSL_NUM_ROOTS, nroot,
                          IMSL_MAX_ITN, max_itn,
                          0);
                                /* Print x */
    imsl_f_write_matrix ("x", 1, 3, x, 0);
}

float fcn(float x)
{
    return  x * x * x + 3.0 * x * x - 4.0 * x - 6.0;
}

Output

                 x
         1           2           3
     1.646      -1.000      -3.646

In the following plot, the initial guesses x = 0.0 and x = 4.6 are marked with hollow circles, and the solutions are marked with filled circles. The other initial guess
x = −193.3 does not fit on this plot.

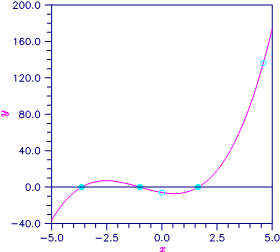
Figure 7- 1 Plot of x3 + 3x2 − 4x − 6

Warning Errors

IMSL_NO_CONVERGE_MAX_ITER              Failure to converge within max_itn             iterations for at least one of the nroot              roots.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260