Solves a system of n nonlinear equations f(x) = 0 using a modified Powell hybrid algorithm.

Synopsis

#include <imsl.h>

float *imsl_f_zeros_sys_eqn (void fcn(), int n, ¼, 0)

The type double function is imsl_d_zeros_sys_eqn.

Required Arguments

void fcn (int n, float x[], float f[])   (Input/Output)
User-supplied function to evaluate the system of equations to be solved, where n is the size of x and f, x is the point at which the functions are evaluated, and f contains the computed function values at the point x.

int n   (Input)
The number of equations to be solved and the number of unknowns.

Return Value

A pointer to the vector x that is a solution of the system of equations. To release this space, use free. If no solution can be computed, then NULL is returned.

Synopsis with Optional Arguments

#include <imsl.h>

float *imsl_f_zeros_sys_eqn (void fcn(), int n,
IMSL_XGUESS, float xguess[],
IMSL_JACOBIAN, void jacobian(),
IMSL_ERR_REL, float err_rel,
IMSL_MAX_ITN, int max_itn,
IMSL_RETURN_USER, float x[],
IMSL_FNORM, float *fnorm,
IMSL_FCN_W_DATA, void fcn ( ), void *data,
IMSL_JACOBIAN_W_DATA, void jacobian(), void *data,
0)

Optional Arguments

IMSL_XGUESS, float xguess[]   (Input)
Array with n components containing the initial estimate of the root.
Default: xguess = 0

IMSL_JACOBIAN, void jacobian (int n, float x[], float fjac[])   (Input/Output)
User-supplied function to evaluate the Jacobian, where n is the number of components in x, x is the point at which the Jacobian is evaluated, and fjac is the computed n ´ n Jacobian matrix at the point x. Note that each derivative
¶fi ∕ ¶xj  should be returned in fjac[(i-1)*n+j-1].

IMSL_ERR_REL, float err_rel   (Input)
Stopping criterion. The root is accepted if the relative error between two successive approximations to this root is less than err_rel.
Default:

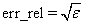
where ɛ is the machine precision

IMSL_MAX_ITN, int max_itn   (Input)
The maximum allowable number of iterations.
Default:  max_itn = 200

IMSL_RETURN_USER, float x[]   (Output)
Array with n components containing the best estimate of the root found by f_zeros_sys_eqn.

IMSL_FNORM, float *fnorm   (Output)
Scalar with the value

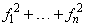
at the point x.

IMSL_FCN_W_DATA, void fcn (int n, float x[], float f[] , void *data) , void *data (Input)
User supplied function to evaluate the system of equations to be solved, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.  See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_JACOBIAN_W_DATA, void jacobian (int m, int n, float x[], float fjac[], int fjac_col_dim, void *data), void *data  (Input)
User supplied function to compute the Jacobian, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.  See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

Description

The function imsl_f_zeros_sys_eqn is based on the MINPACK subroutine HYBRDJ, which uses a modification of the hybrid algorithm due to M.J.D. Powell. This algorithm is a variation of Newton’s method, which takes precautions to avoid undesirable large steps or increasing residuals. For further description, see Moré et al. (1980).

Examples

Example 1

The following 2 ´ 2 system of nonlinear equations

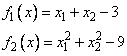
is solved.

#include <imsl.h>
#include <stdio.h>

#define N       2

void            fcn(int, float[], float[]);

void main()
{
    float       *x;

    x = imsl_f_zeros_sys_eqn(fcn, N, 0);
    imsl_f_write_matrix("The solution to the system is", 1, N, x, 0);
}


void fcn(int n, float x[], float f[])
{
    f[0] = x[0] + x[1] - 3.0;
    f[1] = x[0]*x[0] + x[1] * x[1] - 9.0;
}

Output

The solution to the system is
            1           2
            0           3

Example 2

The following 3 ´ 3 system of nonlinear equations

is solved with the initial guess (4.0, 4.0, 4.0).

#include <imsl.h>
#include <stdio.h>
#include <math.h>

#define N       3

void            fcn(int, float[], float[]);

void main()
{
    int         maxitn = 100;
    float       *x, err_rel = 0.0001, fnorm;
    float       xguess[N] = {4.0, 4.0, 4.0};

    x = imsl_f_zeros_sys_eqn(fcn, N,
                             IMSL_ERR_REL, err_rel,
                             IMSL_MAX_ITN, maxitn,
                             IMSL_XGUESS, xguess,
                             IMSL_FNORM, &fnorm,
                             0);
    imsl_f_write_matrix("The solution to the system is", 1, N, x, 0);
    printf("\nwith fnorm = %5.4f\n", fnorm);
}


void fcn(int n, float x[], float f[])
{
    f[0] = x[0] + exp(x[0] - 1.0) + (x[1] + x[2]) * (x[1] + x[2]) - 27.0;
    f[1] = exp(x[1] - 2.0) / x[0] + x[2] * x[2] - 10.0;
    f[2] = x[2] + sin(x[1] - 2.0) + x[1] * x[1] - 7.0;   
}

Output

The solution to the system is
      1           2           3
      1           2           3

with fnorm = 0.0000

Warning Errors

IMSL_TOO_MANY_FCN_EVALS                  The number of function evaluations has exceeded max_itn. A new initial guess may be tried.

IMSL_NO_BETTER_POINT                         Argument err_rel is too small. No further improvement in the approximate solution is possible.

IMSL_NO_PROGRESS                                   The iteration has not made good progress. A new initial guess may be tried.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260