anova_nested

Chapter 4: Analysis of Variance and Designed Experiments

anova_nested

Analyzes a completely nested random model with possibly unequal numbers in the subgroups.

Synopsis

#include <imsls.h>

float *imsls_f_anova_nested (int n_factors, int equal_option, int n_levels[], float y[], ..., 0)

The type double function is imsls_d_anova_nested.

Required Arguments

int n_factors (Input)
Number of factors (number of subscripts) in the model, including error.

int equal_option (Input)
Equal numbers option.

equal_option Description

0 Unequal numbers in the subgroups

1 Equal numbers in the subgroups

int n_levels[] (Input)
Array with the number of levels.

If equal_option = 1, n_levels is of length n_factors and contains the number of levels for each of the factors. In this case, the following additional variables are referred to in the description of anova_nested:

Variable Description

LNL n_levels[0] + n_levels[0] * n_levels[1] + ... + n_levels[0] * n_levels[1] * ... * n_levels[n_factors – 2]

LNLNF n_levels[0] * n_levels[1] * ...* n_levels[n_factors – 2]

NOBS The number of observations. NOBS equals n_levels[0] * n_levels[1] * ... * n_levels[n_factors-1].

If equal_option = 0, n_levels contains the number of levels of each factor at each level of the factor in which it is nested. In this case, the following additional variables are referred to in the description of anova_nested:

Variable Description

LNL Length of n_levels.

LNLNF Length of the subvector of n_levels for the last factor.

NOBS Number of observations. NOBS equals the sum of the last LNLNF elements of n_levels.

For example, a random one-way model with two groups, five responses in the first group and ten in the second group, would have LNL= 3, LNLNF= 2, NOBS = 15, n_levels[0] = 2, n_levels[1] = 5, and
n_levels[2] = 10.

float y[] (Input)
Array of length NOBS containing the responses. The elements of Y are ordered lexicographically, i.e., the last model subscript changes most rapidly, the next to last model subscript changes the next most rapidly, and so forth, with the first subscript changing the slowest.

Return Value

The p-value for the F-statistic, anova_table[9].

Synopsis with Optional Arguments

#include <imsls.h>

float * imsls_f_anova_nested (int n_factors, int equal_option, int n_levels[], float y[],

IMSLS_ANOVA_TABLE, float **anova_table,

IMSLS_ANOVA_TABLE_USER, float anova_table[]
IMSLS_CONFIDENCE, float confidence, IMSLS_VARIANCE_COMPONENTS, float **variance_components, IMSLS_VARIANCE_COMPONENTS_USER, float variance_components[], IMSLS_EMS, float **expect_mean_sq, IMSLS_EMS_USER, float expect_mean_sq[], IMSLS_Y_MEANS, float **y_means, IMSLS_Y_MEANS_USER, float y_means[],
0)

Optional Arguments

IMSLS_ANOVA_TABLE, float **anova_table, (Output)
Address of a pointer to an internally allocated array of size 15
containing the analysis of variance table. The analysis of variance statistics are as follows:

Element Analysis of Variance Statistics

0 Degrees of freedom for the model

1 Degrees of freedom for error

2 Total (corrected) degrees of freedom

3 Sum of squares for the model

4 Sum of squares for error

5 Total (corrected) sum of squares

6 Model mean square

7 Error mean square

8 Overall F-statistic

9 p-value

10 R2 (in percent)

11 Adjusted R2 (in percent)

12 Estimate of the standard deviation

13 Overall mean of y

14 Coefficient of variation (in percent)

IMSLS_ANOVA_TABLE_USER, float anova_table[] (Output)
Storage for array anova_table is provided by the user.
See IMSLS_ANOVA_TABLE.

IMSLS_CONFIDENCE, float confidence (Input)
Confidence level for two-sided interval estimates on the variance components, in percent. confidence percent confidence intervals are computed, hence, confidence must be in the interval
[0.0, 100.0). confidence often will be 90.0, 95.0,
or 99.0. For one-sided intervals with confidence level ONECL, ONECL in the interval [50.0, 100.0), set
confidence = 100.0 - 2.0 * (100.0 - ONECL).
Default: confidence = 95.0

IMSLS_VARIANCE_COMPONENTS, float **variance_components, (Output) Address to a pointer to an internally allocated array. variance_components is an n_factors by 9 matrix containing statistics relating to the particular variance components in the model. Rows of variance_components correspond to the n_factors factors. Columns of variance_components are as follows:

Column Description

1 Degrees of freedom

2 Sum of squares

3 Mean squares

4 F -statistic

5 p-value for F test

6 Variance component estimate

7 Percent of variance of variance explained by variance component

8 Lower endpoint for a confidence interval on the variance component

9 Upper endpoint for a confidence interval on the variance component

A test for the error variance equal to zero cannot be performed. variance_components(n_factors, 4) and variance_components(n_factors, 5) are set to NaN (not a number).

IMSLS_VARIANCE_COMPONENTS_USER, float variance_components[] (Output) Storage for array variance_components is provided by the user. See IMSLS_VARIANCE_COMPONENTS.

IMSLS_EMS, float **expect_mean_sq, (Output) Address to a pointer to an internally allocated array of length
with expected mean square coefficients.

IMSLS_EMS_USER, float expect_mean_sq[], (Output) Storage for array expect_mean_sq is provided by the user.
See IMSLS_EMS.

IMSLS_Y_MEANS, float **y_means (Output)
Address to a pointer to an internally allocated array containing the subgroup means.

Equal options Length of y means

0 1 + n_levels[0] + n_levels[1] + … n_levels[(LNL - LNLNF)-1] (See the description of argument n_levels for definitions of LNL and LNLNF.)

1 1 + n_levels[0] + n_levels[0] * n_levels[1] + … + n_levels[0]* n_levels[1] * … * n_levels[n_factors – 2]

If the factors are labeled A, B, C, and error, the ordering of the means is grand mean, A means, AB means, and then ABC means.

IMSLS_Y_MEANS_USER, float y_means[], Storage for array y_means
is provided by the user. See IMSLS_Y_MEANS

Description

Routine imsls_f_anova_nested analyzes a nested random model with equal or unequal numbers in the subgroups. The analysis includes an analysis of variance table and computation of subgroup means and variance component estimates. Anderson and Bancroft (1952, pages 325−330) discuss the methodology. The analysis of variance method is used for estimating the variance components. This method solves a linear system in which the mean squares are set to the expected mean squares. A problem that Hocking (1985, pages
324−330) discusses is that this method can yield negative variance component estimates. Hocking suggests a diagnostic procedure for locating the cause of a negative estimate. It may be necessary to reexamine the assumptions of the model.

Example 1

An analysis of a three-factor nested random model with equal numbers in the subgroups is performed using data discussed by Snedecor and Cochran (1967, Table 10.16.1, pages 285−288). The responses are calcium concentrations
(in percent, dry basis) as measured in the leaves of turnip greens. Four plants are taken at random, then three leaves are randomly selected from each plant.
Finally, from each selected leaf two samples are taken to determine calcium concentration. The model is

yijk = m + ai + bij + eijk i = 1, 2, 3, 4; j = 1, 2, 3; k = 1, 2

where yijk is the calcium concentration for the k-th sample of the j-th leaf of the
i-th plant, the ai’s are the plant effects and are taken to be independently distributed

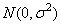
the bij’s are leaf effects each independently distributed

and the eijk’s are errors each independently distributed N(0, s2). The effects are all assumed to be independently distributed. The data are given in the following table:

Plant

Leaf

Samples

3.28

3.52

2.88

3.09

3.48

2.80

2.46

1.87

2.19

2.44

1.92

2.19

2.77

3.74

2.55

2.66

3.44

2.55

3.78

4.07

3.31

3.87

4.12

3.31

#include <imsls.h>

#include <stdio.h>

#define Mfloat float

void main()

{

Mfloat pvalue, *aov, *varc, *ymeans, *ems;

Mfloat y[] = {3.28, 3.09, 3.52, 3.48, 2.88, 2.80, 2.46, 2.44, 1.87,

1.92, 2.19, 2.19, 2.77, 2.66, 3.74, 3.44, 2.55, 2.55, 3.78,

3.87, 4.07, 4.12, 3.31, 3.31};

int n_levels[] = {4, 3, 2};

char *aov_labels[] = {

"degrees of freedom for model",

"degrees of freedom for error",

"total (corrected) degrees of freedom",

"sum of squares for model",

"sum of squares for error",

"total (corrected) sum of squares",

"model mean square",

"error mean square",

"F-statistic",

"p-value",

"R-squared (in percent)",

"adjusted R-squared (in percent)",

"est. standard deviation of within error",

"overall mean of y",

"coefficient of variation (in percent)"};

char *ems_labels[] = {

"Effect A and Error",

"Effect A and Effect B",

"Effect A and Effect A",

"Effect B and Error",

"Effect B and Effect B",

"Error and Error"};

char *means_labels[] = {

"Grand mean",

" A means 1",

" A means 2",

" A means 3",

" A means 4",

"AB means 1 1",

"AB means 1 2",

"AB means 1 3",

"AB means 2 1",

"AB means 2 2",

"AB means 2 3",

"AB means 3 1",

"AB means 3 2",

"AB means 3 3",

"AB means 4 1",

"AB means 4 2",

"AB means 4 3"};

char *components_labels[] = {

"degrees of freedom for A",

"sum of squares for A",

"mean square of A",

"F-statistic for A",

"p-value for A",

"Estimate of A",

"Percent Variation Explained by A",

"95% Confidence Interval Lower Limit for A",

"95% Confidence Interval Upper Limit for A",

"degrees of freedom for B",

"sum of squares for B",

"mean square of B",

"F-statistic for B",

"p-value for B",

"Estimate of B",

"Percent Variation Explained by B",

"95% Confidence Interval Lower Limit for B",

"95% Confidence Interval Upper Limit for B",

"degrees of freedom for Error",

"sum of squares for Error",

"mean square of Error",

"F-statistic for Error",

"p-value for Error",

"Estimate of Error",

"Percent Explained by Error",

"95% Confidence Interval Lower Limit for Error",

"95% Confidence Interval Upper Limit for Error"};

pvalue = imsls_f_anova_nested(3, 1, n_levels, y,

IMSLS_ANOVA_TABLE, &aov,

IMSLS_Y_MEANS, &ymeans,

IMSLS_VARIANCE_COMPONENTS, &varc,

IMSLS_EMS, &ems,

0);

printf("pvalue = %f\n", pvalue);

imsls_f_write_matrix("* * * Analysis of Variance * * *", 15, 1, aov,

IMSLS_ROW_LABELS, aov_labels,

IMSLS_WRITE_FORMAT, "%10.5f",

0);

imsls_f_write_matrix("* * * Expected Mean Square Coefficients * * *"
6, 1, ems,

IMSLS_ROW_LABELS, ems_labels,

IMSLS_WRITE_FORMAT, "%6.2f",

0);

imsls_f_write_matrix("* * * Means * * *", 17, 1, ymeans,

IMSLS_ROW_LABELS, means_labels,

IMSLS_WRITE_FORMAT, "%6.2f",

0);

imsls_f_write_matrix("* * Analysis of Variance / Variance Components * *",

27, 1, varc,

IMSLS_ROW_LABELS, components_labels,

IMSLS_WRITE_FORMAT, "%10.5f",

0);

}

Output

pvalue = 0.079854

* * * Analysis of Variance * * *

degrees of freedom for model 11.00000

degrees of freedom for error 12.00000

total (corrected) degrees of freedom 23.00000

sum of squares for model 10.19054

sum of squares for error 0.07985

total (corrected) sum of squares 10.27040

model mean square 0.92641

error mean square 0.00665

F-statistic 139.21599

p-value 0.00000

R-squared (in percent) 99.22248

adjusted R-squared (in percent) 98.50976

est. standard deviation of within error 0.08158

overall mean of y 3.01208

coefficient of variation (in percent) 2.70826

* * * Expected Mean Square Coefficients * * *

Effect A and Error 1.00

Effect A and Effect B 2.00

Effect A and Effect A 6.00

Effect B and Error 1.00

Effect B and Effect B 2.00

Error and Error 1.00

* * * Means * * *

Grand mean 3.01

A means 1 3.17

A means 2 2.18

A means 3 2.95

A means 4 3.74

AB means 1 1 3.18

AB means 1 2 3.50

AB means 1 3 2.84

AB means 2 1 2.45

AB means 2 2 1.89

AB means 2 3 2.19

AB means 3 1 2.72

AB means 3 2 3.59

AB means 3 3 2.55

AB means 4 1 3.82

AB means 4 2 4.10

AB means 4 3 3.31

* * Analysis of Variance / Variance Components * *

degrees of freedom for A 3.00000

sum of squares for A 7.56034

mean square of A 2.52011

F-statistic for A 7.66516

p-value for A 0.00973

Estimate of A 0.36522

Percent Variation Explained by A 68.53015

95% Confidence Interval Lower Limit for A 0.03955

95% Confidence Interval Upper Limit for A 5.78674

degrees of freedom for B 8.00000

sum of squares for B 2.63020

mean square of B 0.32878

F-statistic for B 49.40642

p-value for B 0.00000

Estimate of B 0.16106

Percent Variation Explained by B 30.22121

95% Confidence Interval Lower Limit for B 0.06967

95% Confidence Interval Upper Limit for B 0.60042

degrees of freedom for Error 12.00000

sum of squares for Error 0.07985

mean square of Error 0.00665

F-statistic for Error ***********

p-value for Error ***********

Estimate of Error 0.00665

Percent Explained by Error 1.24864

95% Confidence Interval Lower Limit for Error 0.00342

95% Confidence Interval Upper Limit for Error 0.01813

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260