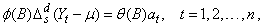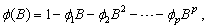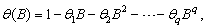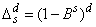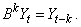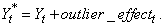Automatically identifies time
series outliers, determines parameters of a multiplicative seasonal ARIMA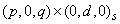 model and produces forecasts
that incorporate the effects of outliers whose effects persist beyond the end of
the series.
model and produces forecasts
that incorporate the effects of outliers whose effects persist beyond the end of
the series.
Synopsis
float *imsls_f_auto_arima (int n_obs, int tpoints[], float x[],...,0)
The type double function is imsls_d_auto_arima.
Required Arguments
int n_obs
(Input)
Number of observations in the original time series. Assuming
that the series is defined at time points 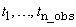 , the actual length of the
series, including missing observations is
, the actual length of the
series, including missing observations is 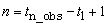 .
.
int tpoints[]
(Input)
A vector of length n_obs containing the
time points 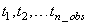 the
time series was observed. It is required that
the
time series was observed. It is required that 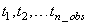 are in strictly ascending
order.
are in strictly ascending
order.
float x[] (Input)
A
vector of length n_obs containing the
observed time series values 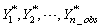 . This series can contain outliers and missing
observations. Outliers are identified by this routine and missing values are
identified by the time values in vector tpoints. If the time
interval between two consecutive time points is greater than one, i.e.
. This series can contain outliers and missing
observations. Outliers are identified by this routine and missing values are
identified by the time values in vector tpoints. If the time
interval between two consecutive time points is greater than one, i.e.
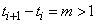 , then
, then 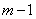 missing values are assumed
to exist between
missing values are assumed
to exist between 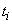 and
and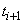 at
times
at
times 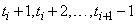 . Therefore, the
gap free series is assumed to be defined for equidistant time points . Missing
values are automatically estimated prior to identifying outliers and producing
forecasts. Forecasts are generated for both missing and observed values.
. Therefore, the
gap free series is assumed to be defined for equidistant time points . Missing
values are automatically estimated prior to identifying outliers and producing
forecasts. Forecasts are generated for both missing and observed values.
Return Value
Pointer to an array of length 1 + p + q with the
estimated constant, AR and MA parameters used to fit the outlier-free series
using an ARIMA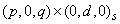 model. Upon completion, if d=model[3]=0, then an ARMA(p, q) model or AR(p) model is fitted to the outlier-free version of the
observed series
model. Upon completion, if d=model[3]=0, then an ARMA(p, q) model or AR(p) model is fitted to the outlier-free version of the
observed series 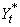 .
If d=model[3]>0, these parameters are computed for an ARMA(p,q) representation of the
seasonally adjusted series
.
If d=model[3]>0, these parameters are computed for an ARMA(p,q) representation of the
seasonally adjusted series 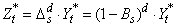 , where
, where 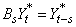 and s=model[2]³1.
and s=model[2]³1.
If
an error occurred, NULL
is returned.
Synopsis with Optional Arguments
float
*imsls_f_auto_arima(int n_obs, int tpoints[], float x[],
IMSLS_RETURN_USER, float
parameters[],
IMSLS_METHOD, int method,
IMSLS_MAX_LAG, int
maxlag,
IMSLS_MODEL, int model[],
IMSLS_DELTA, float
delta,
IMSLS_CRITICAL, float critical,
IMSLS_EPSILON, float
epsilon,
IMSLS_RESIDUAL, float **residual,
IMSLS_RESIDUAL_USER,
float residual[],
IMSLS_RESIDUAL_SIGMA, float
*res_sigma,
IMSLS_NUM_OUTLIERS, int *num_outliers,
IMSLS_P_INITIAL,
int n_p_initial, int p_initial[],
IMSLS_Q_INITIAL, int
n_q_initial, int q_initial[],
IMSLS_S_INITIAL, int n_s_initial,
int s_initial[],
IMSLS_D_INITIAL, int n_d_initial, int
d_initial[],
IMSLS_OUTLIER_STATISTICS, int
**outlier_stat,
IMSLS_OUTLIER_STATISTICS_USER, int
outlier_stat[],
IMSLS_AIC, float *aic,
IMSLS_OUT_FREE_SERIES,
float **outfree_series,
IMSLS_OUT_FREE_SERIES_USER, float
outfree_series[],
IMSLS_CONFIDENCE, float
confidence,
IMSLS_NUM_PREDICT, int
n_predict,
IMSLS_OUT_FREE_FORECAST, float
**outfree_forecast,
IMSLS_OUT_FREE_FORECAST_USER, float
outfree_forecast[],
IMSLS_OUTLIER_FORECAST, float
**outlier_forecast,
IMSLS_OUTLIER_FORECAST_USER, float
outlier_forecast[],
0)
Optional Arguments
IMSLS_METHOD, int
method (Input)
The method used in model selection:
1 —
Automatic ARIMA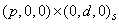 selection
selection
2 — Grid search
Requires arguments
IMSLS_P_INITIAL and IMSLS_Q_INITIAL.
3 — Specified
ARIMA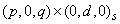 model
model
Requires argument IMSLS_MODEL.
Default: method = 1
For more
information, see the Description section.
IMSLS_MAX_LAG, int maxlag (Input)
The maximum lag allowed when fitting an AR(p) model.
Default:
maxlag = 10
IMSLS_MODEL, int
model[] (Input/Output)
Array of length 4
containing the values for p, q, s, d. If method=3 is chosen,
then the values for p and q must be
defined. If IMSLS_S_INITIAL and IMSLS_D_INITIAL are
not defined, then also s and d
must be given. If method=1 or method=2, then model
is ignored as an input array. On output, model contains the optimum values
for p, q, s, d in model[0], model[1], model[2]
and model[3], respectively.
IMSLS_DELTA, float
delta (Input)
The
dampening effect parameter used in the detection of a Temporary Change Outlier
(TC), 0<delta<1.
Default: delta = 0.7
IMSLS_CRITICAL, float
critical (Input)
Critical value
used as a threshold for outlier detection, critical > 0.
Default: critical = 3.0
IMSLS_EPSILON, float
epsilon (Input)
Positive tolerance value
controlling the accuracy of parameter estimates during outlier
detection.
Default: epsilon = 0.001
IMSLS_RESIDUAL, float
**residual (Output)
Address of a
pointer to an internally allocated array of length 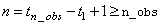 , containing
, containing 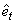 , the estimates of the white
noise in the outlier free original series.
, the estimates of the white
noise in the outlier free original series.
IMSLS_RESIDUAL_USER, float
residual[] (Output)
Storage for array
residual is provided
by the user. See IMSLS_RESIDUAL.
IMSLS_RESIDUAL_SIGMA, float
*res_sigma (Output)
Residual standard
error (RSE) of the outlier free original series.
IMSLS_NUM_OUTLIERS,
int *num_outliers
(Output)
The number of
outliers detected.
IMSLS_P_INITIAL, int
n_p_initial, int
p_initial[] (Input)
An array with n_p_initial elements
containing the candidate values for p, from which the
optimum is being selected. All candidate values in p_initial[] must be
non-negative and n_p_initial ³ 1. If method=2, then IMSLS_P_INITIAL must
be defined. Otherwise, n_p_initial and p_initial are
ignored.
IMSLS_Q_INITIAL,
int n_q_initial,
int q_initial[]
(Input)
An array with n_q_initial elements
containing the candidate values for q, from which the
optimum is being selected. All candidate values in q_initial[] must be
non-negative and n_q_initial ³ 1. If method=2, then IMSLS_Q_INITIAL must
be defined. Otherwise, n_q_initial and q_initial are
ignored.
IMSLS_S_INITIAL,
int n_s_initial,
int s_initial[]
(Input)
A vector of length
n_s_initial containing
the candidate values for s, from which the
optimum is being selected. All candidate values in s_initial[] must be
positive and n_s_initial ³
1.
Default: n_s_initial=1, s_initial={1}
IMSLS_D_INITIAL,
int n_d_initial,
int d_initial[]
(Input)
A vector of length n_d_initial containing
the candidate values for d, from which the optimum is being
selected. All candidate values in d_initial[] must be
non-negative and n_d_initial ³ 1.
Default: n_d_initial=1, d_initial={0}
IMSLS_OUTLIER_STATISTICS,
int **outlier_stat
(Output)
Address of a
pointer to an internally allocated array of length num_outliers by 2
containing outlier statistics. The first column contains the time at which
the outlier was observed (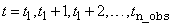 ) and the second column contains
an identifier indicating the type of outlier observed. Outlier types fall
into one of five categories:
) and the second column contains
an identifier indicating the type of outlier observed. Outlier types fall
into one of five categories:
If num_outliers=0, NULL is returned.
IMSLS_OUTLIER_STATISTICS_USER,
int outlier_stat[]
(Output)
A user allocated
array of length n ´ 2 containing
outlier statistics in its first num_outliers rows.
Here, 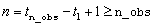 .
.
See IMSLS_OUTLIER_STATISTICS.
If
num_outliers = 0, outlier_stat stays
unchanged.
IMSLS_AIC,
float *aic
(Output)
Akaike’s
information criterion (AIC) for the optimum model.
IMSLS_OUT_FREE_SERIES, float **outfree_series
(Output)
Address of a pointer to an internally allocated array of
length n by 2, where 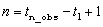 . The first column of outfree_series
contains the n_obs observations
from the original series,
. The first column of outfree_series
contains the n_obs observations
from the original series, 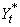 , plus estimated values for any time gaps. The second
column contains the same values as the first column adjusted by removing any
outlier effects. In effect, the second column contains estimates of the
underlying outlier-free series,
, plus estimated values for any time gaps. The second
column contains the same values as the first column adjusted by removing any
outlier effects. In effect, the second column contains estimates of the
underlying outlier-free series, 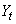 . If no outliers are detected then both columns will
contain identical values.
. If no outliers are detected then both columns will
contain identical values.
IMSLS_OUT_FREE_SERIES_USER,
float outfree_series[]
(Output)
A user allocated array of length n by 2, where 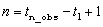 . For further details, see IMSLS_OUT_FREE_SERIES.
. For further details, see IMSLS_OUT_FREE_SERIES.
IMSLS_CONFIDENCE,
float confidence
(Input)
Confidence level for computing forecast confidence limits,
taken from the exclusive interval (0, 100). Typical choices for confidence are 90.0,
95.0 and 99.0.
Default: confidence = 95.0
IMSLS_NUM_PREDICT,
int n_predict
(Input)
The number of forecasts requested. Forecasts are made at
origin 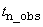 , i.e. from the
last observed value of the series.
, i.e. from the
last observed value of the series.
Default: n_predict = 0
IMSLS_OUT_FREE_FORECAST,
float **outfree_forecast
(Output)
Address of a pointer to an internally allocated array of
length n_predict by 3. The first column contains the forecasted values for the
original outlier free series for t=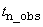 +1,
+1,
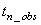 +
2,...,
+
2,..., 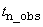 + n_predict. The second column contains standard errors for these forecasts,
and the third column contains the psi weights of the infinite order moving
average form of the model.
+ n_predict. The second column contains standard errors for these forecasts,
and the third column contains the psi weights of the infinite order moving
average form of the model.
IMSLS_OUT_FREE_FORECAST_USER,
float outfree_forecast[]
(Output)
A user allocated array of length n_predict by 3. For more information, see IMSLS_OUT_FREE_FORECAST.
IMSLS_OUTLIER_FORECAST,
float **outlier_forecast
(Output)
Address of a pointer to an internally allocated array of
length n_predict by 3. The first column contains the forecasted values for the
original series for t=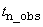 +1,
+1,
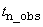 +2,...,
+2,..., 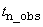 +n_predict. The second column contains standard errors for these forecasts,
and the third column contains the
+n_predict. The second column contains standard errors for these forecasts,
and the third column contains the 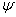 weights of the infinite order moving average form of the model.
weights of the infinite order moving average form of the model.
IMSLS_OUTLIER_FORECAST_USER,
float outlier_forecast[]
(Output)
A user allocated array of length n_predict by 3. For more
information, see IMSLS_OUTLIER_FORECAST.
IMSLS_RETURN_USER,
float x[]
(Output)
A user allocated array containing the estimated constant,
AR and MA parameters in its first 1+p+q locations. The values p
and q can be estimated by upper bounds: If method=1, an upper
bound for p would be maxlag, and
q= 0.
If method=2, upper bounds
for p and q would be the maximum values in arrays p_initial and
q_initial,
respectively. If method=3,
p= model[0] and
q= model[1].
Description
Function imsls_f_auto_arima determines the parameters of a multiplicative seasonal ARIMA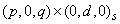 model, and then uses the
fitted model to identify outliers and prepare forecasts. The order of this model
can be specified or automatically determined.
model, and then uses the
fitted model to identify outliers and prepare forecasts. The order of this model
can be specified or automatically determined.
The
ARIMA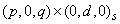 model
handled by imsls_f_auto_arima
has the following form:
model
handled by imsls_f_auto_arima
has the following form:
It is assumed that all roots of 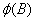 and
and 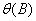 lie outside the unit
circle. Clearly, if
lie outside the unit
circle. Clearly, if 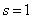 this reduces to the traditional ARIMA(p, d, q) model.
this reduces to the traditional ARIMA(p, d, q) model.
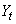 is
the unobserved, outlier-free time series with mean
is
the unobserved, outlier-free time series with mean 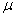 , and white noise
, and white noise 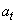 . This model is referred to as
the underlying, outlier-free model. Function imsls_f_auto_arima
does not assume that this series is observable. It assumes that the observed
values might be contaminated by one or more outliers, whose effects are added to
the underlying outlier-free series:
. This model is referred to as
the underlying, outlier-free model. Function imsls_f_auto_arima
does not assume that this series is observable. It assumes that the observed
values might be contaminated by one or more outliers, whose effects are added to
the underlying outlier-free series:
Outlier identification uses the algorithm developed by Chen and Liu (1993). Outliers are classified into 1 of 5 types:
Once outliers are identified, imsls_f_auto_arima
estimates 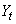 , the
outlier-free series representation of the data, by removing the estimated
outlier effects.
, the
outlier-free series representation of the data, by removing the estimated
outlier effects.
Using the information about the adjusted ARIMA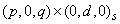 model and the removed outliers, forecasts are then
prepared for the outlier-free series. Outlier effects are added to these
forecasts to produce a forecast for the observed series,
model and the removed outliers, forecasts are then
prepared for the outlier-free series. Outlier effects are added to these
forecasts to produce a forecast for the observed series, 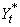 . If there are no outliers,
then the forecasts for the outlier-free series and the observed series will be
identical.
. If there are no outliers,
then the forecasts for the outlier-free series and the observed series will be
identical.
Model Selection
Users have an option of either specifying specific values for p, q , s and d or have imsls_f_auto_arima automatically select best fit values. Model selection can be conducted in one of three methods listed below depending upon the value of variable method.
Method 1: Automatic ARIMA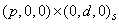 Selection
Selection
This method initially searches for the AR(p) representation with minimum AIC for the noisy data, where p =0,...,maxlag.
If IMSLS_D_INITIAL
is defined then the values in s_initial
and d_initial
are included in the search to find an optimum ARIMA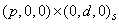 representation of the series.
Here, every possible combination of values for p, s in s_initial
and d in d_initial
is examined. The best found ARIMA
representation of the series.
Here, every possible combination of values for p, s in s_initial
and d in d_initial
is examined. The best found ARIMA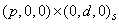 representation is then used as input for the outlier detection
routine.
representation is then used as input for the outlier detection
routine.
The optimum values for p, q, s and d are returned in model[0], model[1], model[2] and model[3], respectively.
Method 2: Grid Search
The second automatic method conducts a grid search for p and q using all possible combinations of candidate values in p_initial and q_initial. Therefore, for this method the definition of IMSLS_P_INITIAL and IMSLS_Q_INITIAL is required.
If IMSLS_D_INITIAL is defined, the grid search is extended to include the candidate values for s and d given in s_initial and d_initial, respectively.
If IMSLS_D_INITIAL is not defined, no seasonal adjustment is attempted, and the grid search is restricted to searching for optimum values of p and q only.
The optimum values of p, q, s and d are returned in model[0], model[1], model[2] and model[3], respectively.
Method 3: Specified ARIMA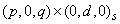 Model
Model
In the third method, specific values for p, q, s and
d are given. The
values for p and
q must be
defined in model[0] and model[1],
respectively. If IMSLS_S_INITIAL
and IMSLS_D_INITIAL
are not defined, then values 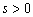 and
and 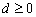 must be specified in model[2]
and model[3]. If IMSLS_S_INITIAL
and IMSLS_D_INITIAL are defined, then a grid
search for the optimum values of s and d is conducted using all possible
combinations of input values in s_initial
and d_initial.
The optimum values of s and d can be found in model[2]
and model[3],
respectively.
must be specified in model[2]
and model[3]. If IMSLS_S_INITIAL
and IMSLS_D_INITIAL are defined, then a grid
search for the optimum values of s and d is conducted using all possible
combinations of input values in s_initial
and d_initial.
The optimum values of s and d can be found in model[2]
and model[3],
respectively.
Outliers
The algorithm of Chen and Liu (1993) is used to identify outliers. The number of outliers identified is returned in num_outliers. Both the time and classification for these outliers are returned in outlier_stat[]. Outliers are classified into one of five categories based upon the standardized statistic for each outlier type. The time at which the outlier occurred is given in the first column of outlier_stat. The outlier identifier returned in the second column is according to the descriptions in the following table:
Except for additive outliers (AO), the effect of an outlier persists to observations following that outlier. Forecasts produced by imsls_f_auto_arima take this into account.
Examples
Example 1
This example uses time series LNU03327709 from the US Department of Labor, Bureau of Labor Statistics. It contains the unadjusted special unemployment rate, taken monthly from Janurary 1994 through September 2005. The values 01/2004 – 03/2005 are used by imsls_f_auto_arima for outlier detection and parameter estimation. In this example, Method 1 without seasonal adjustment is chosen to find an appropriate AR(p) model. A forecast is done for the following six months and compared with the actual values 04/2005 – 09/2005.
float *parameters = NULL, *outlier_forecast = NULL;
int n_obs, n_predict, i, num_outliers;
12.8,12.2,11.9,10.9,10.6,11.3,11.1,10.4,10.0,9.7,9.7,9.7,
11.1,10.5,10.3,9.8,9.8,10.4,10.4,10.0,9.7,9.3,9.6,9.7,
10.8,10.7,10.3,9.7,9.5,10.0,10.0,9.3,9.0,8.8,8.9,9.2,
10.4,10.0,9.6,9.0,8.5,9.2,9.0,8.6,8.3,7.9,8.0,8.2,
9.3,8.9,8.9,7.7,7.6,8.4,8.5,7.8,7.6,7.3,7.2,7.3,
8.5,8.2,7.9,7.4,7.1,7.9,7.7,7.2,7.0,6.7,6.8,6.9,
7.8,7.6,7.4,6.6,6.8,7.2,7.2,7.0,6.6,6.3,6.8,6.7,
8.1,7.9,7.6,7.1,7.2,8.2,8.1,8.1,8.2,8.7,9.0,9.3,
10.5,10.1,9.9,9.4,9.2,9.8,9.9,9.5,9.0,9.0,9.4,9.6,
11.0,10.8,10.4,9.8,9.7,10.6,10.5,10.0,9.8,9.5,9.7,9.6,
10.9,10.3,10.4,9.3,9.3,9.8,9.8,9.3,8.9,9.1,9.1,9.1,
10.2,9.9,9.4,8.7,8.6,9.3,9.1,8.8,8.5};
13,14,15,16,17,18,19,20,21,22,23,24,
25,26,27,28,29,30,31,32,33,34,35,36,
37,38,39,40,41,42,43,44,45,46,47,48,
49,50,51,52,53,54,55,56,57,58,59,60,
61,62,63,64,65,66,67,68,69,70,71,72,
73,74,75,76,77,78,79,80,81,82,83,84,
85,86,87,88,89,90,91,92,93,94,95,96,
97,98,99,100,101,102,103,104,105,106,107,108,
109,110,111,112,113,114,115,116,117,118,119,120,
121,122,123,124,125,126,127,128,129,130,131,132,
133,134,135,136,137,138,139,140,141};
parameters = imsls_f_auto_arima(n_obs, times, x, IMSLS_MODEL, model,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS, &outlier_stat,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_OUTLIER_FORECAST, &outlier_forecast,
printf("\nMethod 1: Automatic ARIMA model selection,"
printf("\nModel chosen: p=%d, q=%d, s=%d, d=%d\n", model[0],
model[1], model[2], model[3]);
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n\n");
printf("Time point\t\tOutlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d\t\t%d\n", outlier_stat[2*i], outlier_stat[2*i+1]);
printf("RSE = %lf\n\n", res_sigma);
for (i=0; i<=model[0]+model[1]; i++)
printf("parameters[%d]=%lf\n", i, parameters[i]);
forecast_table[4*i] = x[n_obs+i];
forecast_table[4*i+1] = outlier_forecast[3*i];
forecast_table[4*i+2] = outlier_forecast[3*i+1];
forecast_table[4*i+3] = outlier_forecast[3*i+2];
imsls_f_write_matrix("\t* * * Forecast Table * * *"
"\nOrig. series\t forecast\tprob. limits\tpsi weights\n",
n_predict, 4, forecast_table, IMSLS_WRITE_FORMAT, "%11.4f", 0);
Output
Method 1: Automatic ARIMA model selection, no differencing
Model chosen: p=5, q=0, s=1, d=0
Orig. series forecast prob. limits psi weights
Example 2
This is the same as Example 1,
except now imsls_f_auto_arima
uses Method 2 with a possible seasonal adjustment. As a result,
the unadjusted model with 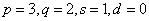 is chosen as optimum.
is chosen as optimum.
int n_obs, n_predict, i, num_outliers;
int n_p_initial = 4, n_q_initial = 4;
float outfree_series_user[282];
float outlier_forecast_user[24];
12.8,12.2,11.9,10.9,10.6,11.3,11.1,10.4,10.0,9.7,9.7,9.7,
11.1,10.5,10.3,9.8,9.8,10.4,10.4,10.0,9.7,9.3,9.6,9.7,
10.8,10.7,10.3,9.7,9.5,10.0,10.0,9.3,9.0,8.8,8.9,9.2,
10.4,10.0,9.6,9.0,8.5,9.2,9.0,8.6,8.3,7.9,8.0,8.2,
9.3,8.9,8.9,7.7,7.6,8.4,8.5,7.8,7.6,7.3,7.2,7.3,
8.5,8.2,7.9,7.4,7.1,7.9,7.7,7.2,7.0,6.7,6.8,6.9,
7.8,7.6,7.4,6.6,6.8,7.2,7.2,7.0,6.6,6.3,6.8,6.7,
8.1,7.9,7.6,7.1,7.2,8.2,8.1,8.1,8.2,8.7,9.0,9.3,
10.5,10.1,9.9,9.4,9.2,9.8,9.9,9.5,9.0,9.0,9.4,9.6,
11.0,10.8,10.4,9.8,9.7,10.6,10.5,10.0,9.8,9.5,9.7,9.6,
10.9,10.3,10.4,9.3,9.3,9.8,9.8,9.3,8.9,9.1,9.1,9.1,
10.2,9.9,9.4,8.7,8.6,9.3,9.1,8.8,8.5};
13,14,15,16,17,18,19,20,21,22,23,24,
25,26,27,28,29,30,31,32,33,34,35,36,
37,38,39,40,41,42,43,44,45,46,47,48,
49,50,51,52,53,54,55,56,57,58,59,60,
61,62,63,64,65,66,67,68,69,70,71,72,
73,74,75,76,77,78,79,80,81,82,83,84,
85,86,87,88,89,90,91,92,93,94,95,96,
97,98,99,100,101,102,103,104,105,106,107,108,
109,110,111,112,113,114,115,116,117,118,119,120,
121,122,123,124,125,126,127,128,129,130,131,132,
133,134,135,136,137,138,139,140,141};
imsls_f_auto_arima(n_obs, times, x, IMSLS_MODEL, model,
IMSLS_P_INITIAL, n_p_initial, p_initial,
IMSLS_Q_INITIAL, n_q_initial, q_initial,
IMSLS_S_INITIAL, n_s_initial, s_initial,
IMSLS_D_INITIAL, n_d_initial, d_initial,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS_USER, outlier_stat_user,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_OUTLIER_FORECAST_USER, outlier_forecast_user,
IMSLS_RETURN_USER, parameters_user,
forecast_table[4*i] = x[n_obs+i];
forecast_table[4*i+1] = outlier_forecast_user[3*i];
forecast_table[4*i+2] = outlier_forecast_user[3*i+1];
forecast_table[4*i+3] = outlier_forecast_user[3*i+2];
printf("\nMethod 2: Grid search, differencing allowed\n");
printf("\nModel chosen: p=%d, q=%d, s=%d, d=%d\n", model[0],
model[1], model[2], model[3]);
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n\n");
printf("Time point\t\tOutlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d\t\t%d\n", outlier_stat_user[2*i],
printf("RSE = %lf\n\n", res_sigma);
for (i=0; i<=model[0]+model[1]; i++)
printf("parameters[%d]=%lf\n", i, parameters_user[i]);
imsls_f_write_matrix("\n\t* * * Forecast Table * * *"
"\nOrig. series\t forecast\tprob. limits\tpsi weights\n",
n_predict, 4, forecast_table, IMSLS_WRITE_FORMAT, "%11.4f", 0);
Output
Method 2: Grid search, differencing allowed
Model chosen: p=3, q=2, s=1, d=0
Orig. series forecast prob. limits psi weights
Example 3
This example is the same as Example 2 but
now Method 3 with the optimum model parameters 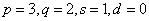 from Example 2 are chosen
for outlier detection and forecasting.
from Example 2 are chosen
for outlier detection and forecasting.
float *parameters = NULL, *outlier_forecast = NULL;
int n_obs, n_predict, i, num_outliers;
12.8,12.2,11.9,10.9,10.6,11.3,11.1,10.4,10.0,9.7,9.7,9.7,
11.1,10.5,10.3,9.8,9.8,10.4,10.4,10.0,9.7,9.3,9.6,9.7,
10.8,10.7,10.3,9.7,9.5,10.0,10.0,9.3,9.0,8.8,8.9,9.2,
10.4,10.0,9.6,9.0,8.5,9.2,9.0,8.6,8.3,7.9,8.0,8.2,
9.3,8.9,8.9,7.7,7.6,8.4,8.5,7.8,7.6,7.3,7.2,7.3,
8.5,8.2,7.9,7.4,7.1,7.9,7.7,7.2,7.0,6.7,6.8,6.9,
7.8,7.6,7.4,6.6,6.8,7.2,7.2,7.0,6.6,6.3,6.8,6.7,
8.1,7.9,7.6,7.1,7.2,8.2,8.1,8.1,8.2,8.7,9.0,9.3,
10.5,10.1,9.9,9.4,9.2,9.8,9.9,9.5,9.0,9.0,9.4,9.6,
11.0,10.8,10.4,9.8,9.7,10.6,10.5,10.0,9.8,9.5,9.7,9.6,
10.9,10.3,10.4,9.3,9.3,9.8,9.8,9.3,8.9,9.1,9.1,9.1,
10.2,9.9,9.4,8.7,8.6,9.3,9.1,8.8,8.5};
13,14,15,16,17,18,19,20,21,22,23,24,
25,26,27,28,29,30,31,32,33,34,35,36,
37,38,39,40,41,42,43,44,45,46,47,48,
49,50,51,52,53,54,55,56,57,58,59,60,
61,62,63,64,65,66,67,68,69,70,71,72,
73,74,75,76,77,78,79,80,81,82,83,84,
85,86,87,88,89,90,91,92,93,94,95,96,
97,98,99,100,101,102,103,104,105,106,107,108,
109,110,111,112,113,114,115,116,117,118,119,120,
121,122,123,124,125,126,127,128,129,130,131,132,
133,134,135,136,137,138,139,140,141};
parameters = imsls_f_auto_arima(n_obs, times, x, IMSLS_MODEL, model,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS, &outlier_stat,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_OUTLIER_FORECAST, &outlier_forecast,
printf("\nMethod 3: Specified ARIMA model\n");
printf("\nModel: p=%d, q=%d, s=%d, d=%d\n", model[0], model[1],
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n\n");
printf("Time point\t\tOutlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d\t\t%d\n", outlier_stat[2*i], outlier_stat[2*i+1]);
printf("RSE = %lf\n", res_sigma);
for (i=0; i<=model[0]+model[1]; i++)
printf("parameters[%d]=%lf\n", i, parameters[i]);
forecast_table[4*i] = x[n_obs+i];
forecast_table[4*i+1] = outlier_forecast[3*i];
forecast_table[4*i+2] = outlier_forecast[3*i+1];
forecast_table[4*i+3] = outlier_forecast[3*i+2];
imsls_f_write_matrix("\t* * * Forecast Table * * *"
"\nOrig. series\t forecast\tprob. limits\tpsi weights\n",
n_predict, 4, forecast_table, IMSLS_WRITE_FORMAT, "%11.4f", 0);
Output
Method 3: Specified ARIMA model
Orig. series forecast prob. limits psi weights
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |