.p>.CSCH11.DOC!BETA_INVERSE_CDF;beta_inverse_cdf
Evaluates the inverse of the beta distribution function.
Synopsis
#include <imsls.h>
float imsls_f_beta_inverse_cdf (float p, float pin, float qin)
The type double function is imsls_d_beta_inverse_cdf.
Required Arguments
float p
(Input)
Probability for which the inverse of the beta distribution function
is to be evaluated.
Argument p must be in the open
interval (0.0, 1.0).
float pin
(Input)
First beta distribution parameter. Argument pin must be
positive.
float qin
(Input)
Second beta distribution parameter. Argument qin must be
positive.
Return Value
Function imsls_f_beta_inverse_cdf returns the inverse distribution function of a beta random variable with parameters pin and qin.
Description
With P = p, p = pin, and q = qin, the beta_inverse_cdf returns x such that
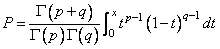
where Γ (×) is the gamma function. The probability that the random variable takes a value less than or equal to x is P.
Example
Suppose X is a beta random variable with parameters 12 and 12 (X has a symmetric distribution). In this example, we find the value x such that the probability that X is less than or equal to x is 0.9.
#include
<imsls.h>
main()
{
float p, pin, qin,
x;
pin =
12.0;
qin =
12.0;
p =
0.9;
x =
imsls_f_beta_inverse_cdf(p, pin,
qin);
printf(" X is less than
%6.4f with probability
0.9.\n",
x);
}
Output
X is less than 0.6299 with probability 0.9.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |