Evaluates the bivariate normal distribution function.

Synopsis

#include <imsls.h>

float imsls_f_bivariate_normal_cdf (float x, float y, float rho)

The type double function is imsls_d_bivariate_normal_cdf.

Required Arguments

float x   (Input)
The x-coordinate of the point for which the bivariate normal distribution function is to be evaluated.

float y   (Input)
The y-coordinate of the point for which the bivariate normal distribution function is to be evaluated.

float rho   (Input)
Correlation coefficient.

Return Value

The probability that a bivariate normal random variable with correlation rho takes a value less than or equal to x and less than or equal to y.

Description

Function imsls_f_bivariate_normal_cdf evaluates the distribution function F of a bivariate normal distribution with means of zero, variances of one, and correlation of rho; that is, with r = rho, and |r| < 1,

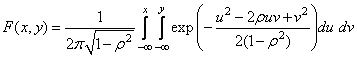
To determine the probability that U £ u0 and V £ v0, where (U, V)T is a bivariate normal random variable with mean m = (mU, mV)T and variance-covariance matrix

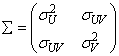
transform (U, V)T to a vector with zero means and unit variances. The input
to imsls_f_bivariate_normal_cdf would be X = (u0 - mU)/sU, Y = (v0 - mV)/sV, and r = sUV/(sUsV).

Function imsls_f_bivariate_normal_cdf uses the method of Owen (1962, 1965). Computation of Owen’s T-function is based on code by M. Patefield and D. Tandy (2000). For |r| = 1, the distribution function is computed based on the univariate statistic, Z = min(x, y), and on the normal distribution function imsls_f_normal_cdf.

Example

Suppose (X, Y) is a bivariate normal random variable with mean (0, 0) and variance-covariance matrix as follows:

In this example, we find the probability that X is less than −2.0 and Y is less than 0.0.

#include <imsls.h>

main()
{
        float           p, rho, x, y;

        x = -2.0;
        y = 0.0;
        rho = 0.9;
        p = imsls_f_bivariate_normal_cdf(x, y, rho);
        printf(" The probability that X is less than -2.0\n"
               " and Y is less than 0.0 is %6.4f\n", p);

}

Output

The probability that X is less than -2.0
and Y is less than 0.0 is 0.0228

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260