Analyzes data from balanced and unbalanced completely randomized experiments. Funtion crd_factorial does permit a factorial treatment structure. However, unlike anova_factorial, function crd_factorial allows for missing data, unequal replication and one or more locations.
Synopsis
#include <imsls.h>
float * imsls_f_crd_factorial (int n_obs, int n_locations,
int n_factors, int n_levels[],
int
model[], float y[],…, 0)
The type double function is imsls_d_crd_factorial.
Required Arguments
int n_obs
(Input)
Number of missing and non-missing experimental
observations.
int n_locations
(Input)
Number of locations. n_locations must be
one or greater.
int n_factors
(Input)
Number of factors in the model.
int n_levels[]
(Input)
Array of length n_factors+1. The
n_levels[0]
through n_levels[n_factors-1] contain
the number of levels for each factor. The last element, n_levels[n_factors], contains
the number of replicates for each treatment combination within a location.
int model[] (Input)
A
n_obs by (n_factors+1) array
identifying the location and factor levels associated with each
observation in y. The first
column must contain the location identifier and the remaining columns the factor
level identifiers in the same order used in n_levels. If
n_locations = 1,
the first column is still required, but its contents are ignored.
float y[] (Input)
An aray
of length n_obs
containing the experimental observations and any missing values. Missing
values are indicated by placing a NaN (not a number) in y. The NaN value can
be set using either the function imsls_f_machine(6) or
imsls_d_machine(6),
depending upon whether single or double precision is being used,
respectively.
Return Value
A pointer to the memory location of a two dimensional, n_anova by 6 array containing the ANOVA table, where:
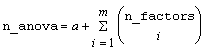 ,
,
where
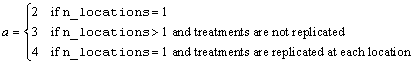
Each row in this array contains values for one of the effects in the ANOVA table. The first value in each row, anova_tablei,0 = anova_table[i*6], is the source identifier which identifies the type of effect associated with values in that row. The remaining values in a row contain the ANOVA table values using the following convention:
|
J |
anova_tablei,j = anova_table[i*6+j] |
|
0 |
Source Identifier (values described below) |
|
1 |
Degrees of freedom |
|
2 |
Sum of squares |
|
3 |
Mean squares |
|
4 |
F-statistic |
|
5 |
p-value for this F-statistic |
The values for the mean squares, F-statistic and p-value are set to NaN for the residual and corrected total effects.
The Source Identifiers in the first column of anova_tablei,j are the only negative values in anova_table. The absolute value of the source identifier is equal to the order of the effect in that row. Main effects, for example, have a source identifier of –1. Two-way interactions use a source identifier of –2, and so on.
|
Source Identifier |
|
|
-1 |
Main Effects † |
|
-2 |
Two-Way Interactions ‡ |
|
-3 |
Three-Way Interactions ‡ |
|
. |
. |
|
. |
. |
|
. |
. |
|
-n_factors |
(n_factors)-way Interactions ‡ |
|
-n_factors-1 |
Effects Error Term |
|
-n_factors-2 |
Residual Ý |
|
-n_factors-3 |
Corrected Total |
Notes: By default, model_order = n_factors when treatments are replicated, or n_locations >1. However, if treatments are not replicated and n_locations =1, model_order = n_factors -1.
† The number of main effects is equal to n_factors+1 if n_locations >1, and n_factors if n_locations =1. The first row of values, anova_table[0] through anova_table[5] contain the location effect if n_locations >1. If n_locations=1, then these values are the effects for factor 1.
Ý The residual term is only provided when treatments are replicated, i.e., n_levels[n_factors]>1.
‡ The number of interaction effects for the nth-way interactions is equal to
 .
.
The order of these terms is in ascending order by treatment subscript. The interactions for factor 1 appear first, followed by factor 2, factor 3, and so on.
Synopsis with Optional Arguments
#include <imsls.h>
float *
imsls_f_crd_factorial (int
n_obs,
int n_locations,
int
n_factors,
int n_levels[], int
model[],
float y[],
IMSLS_RETURN_USER,
float anova_table[]
IMSLS_N_MISSING, int
*n_missing,
IMSLS_CV, float
*cv,
IMSLS_GRAND_MEAN, float
*grand_mean,
IMSLS_FACTOR_MEANS, float
**factor_means,
IMSLS_FACTOR_MEANS_USER, float
factor_means[],
IMSLS_FACTOR_STD_ERRORS, float
**factor_std_err,
IMSLS_FACTOR_STD_ERRORS_USER,
float factor_std_err[],
IMSLS_TWO_WAY_MEANS,
float **two_way_means,
IMSLS_TWO_WAY_MEANS_USER,
float two_way_means[],
IMSLS_TWO_WAY_STD_ERRORS, float
**two_way_std_err,
IMSLS_TWO_WAY_STD_ERRORS_USER, float
two_way_std_err[],
IMSLS_TREATMENT_MEANS, float
**treatment_means,
IMSLS_TREATMENT_MEANS_USER, float
treatment_means[],
IMSLS_TREATMENT_STD_ERROR, float
**treatment_std_err,
IMSLS_TREATMENT_STD_ERROR_USER,
float
treatment_std_err[],
IMSLS_ANOVA_ROW_LABELS, char
***anova_row_labels
IMSLS_ANOVA_ROW_LABELS_USER, char
*anova_row_labels[],
0)
Optional Arguments
IMSLS_RETURN_USER,
float
anova_table[] (Output)
User defined n_anova by 6 array for
the anova_table.
IMSLS_N_MISSING, int
*n_missing (Output)
Number of missing
values, if any, found in y. Missing
values are denoted with a NaN (Not a Number) value.
IMSLS_CV, float
*cv
(Output)
Coefficient of Variation computed by:
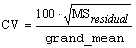
IMSLS_GRAND_MEAN, float *grand_mean
(Output)
Mean of all the data across every location.
IMSLS_FACTOR_MEANS, float **factor_means
(Output)
Address of a pointer to an internally allocated array
of length n_levels[0]+n_levels[1]+…+n_levels[n_factors-1] containing the
factor means.
IMSLS_FACTOR_MEANS_USER, float factor_means[]
(Output)
Storage for the array factor_means, provided
by the user.
IMSLS_FACTOR_STD_ERRORS, float
**factor_std_err (Output)
Address of a pointer to an
internally allocated n_factors by 2 array
containing factor standard errors and their associated degrees of freedom.
The first column contains the standard errors for comparing two factor means and
the second its associated degrees of freedom.
IMSLS_FACTOR_STD_ERRORS_USER,
float factor_std_err[]
(Output)
Storage for the array factor_std_err,
provided by the user.
IMSLS_TWO_WAY_MEANS,
float
**two_way_means (Output)
Address of a pointer to an
internally allocated one-dimensional array containing the two-way means for all
two by two combinations of the factors. The total length of this array
when n_factors >
1 is equal to:

If n_factors = 1, NULL is returned. If n_factors>1, the means would first be produced for all combinations of the first two factors followed by all combinations of the remaining factors using the subscript order suggested by the above formula. For example, if the experiment is a 2x2x2 factorial, the 12 two-way means would appear in the following order: A1B1, A1B2, A2B1, A2B2, A1C1, A1C2, A2C1, A2C2, B1C1, B1C2, B2C1, and B2C2.
IMSLS_TWO_WAY_MEANS_USER,
float
two_way_means[] (Output)
Storage for the array two_way_means,
provided by the user.
IMSLS_TWO_WAY_STD_ERRORS,
float
**two_way_std_err (Output)
Address of a pointer to an
internally allocated n_two_way by 2 array
containing factor standard errors and their associated degrees of freedom.,
where
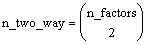
The first column contains the standard errors for comparing two 2-way
interaction means and the second its associated degrees of freedom. The
ordering of the rows in this array is similar to that used in
IMSLS
TWO_WAY_MEANS. For example if n_factors=4, then
n_two_way =6
with the order AB, AC, AD, BC, BD, CD.
IMSLS_TWO_WAY_STD_ERRORS_USER,
float two_way_std_err[]
(Output)
Storage for the array two_way_std_err,
provided by the user.
IMSLS_TREATMENT_MEANS,
float
**treatment_means (Output)
Address of a pointer to an
internally allocated array of size
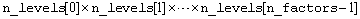
containing the treatment means. The order of the means is organized in ascending order by the value of the factor identifier. For example, if the experiment is a 2x2x2 factorial, the 8 means would appear in the following order: A1B1C1, A1B1C2, A1B2C1, A1B1C2, A2B1C1, A2B1C2, A2B2C1, and A2B2C2.
IMSLS_TREATMENT_MEANS_USER,
float treatment_means[]
(Output)
Storage for the array treatment_means,
provided by the user.
IMSLS_TREATMENT_STD_ERROR, float
**treatment_std_err (Output)
The array of length 2
containing standard error for comparing treatments based upon the average number
of replicates per treatment and its associated degrees of freedom.
IMSLS_TREATMENT_STD_ERROR_USER,
float treatment_std_err[]
(Output)
Storage for the array treatment_std_err, provided by the
user.
IMSLS_ANOVA_ROW_LABELS, char
***anova_row_labels (Output)
Address of a pointer to a
pointer to an internally allocated array containing the labels for each of
the n_anova rows of the
returned ANOVA table. The label for the i-th
row of the ANOVA table can be printed with printf("%s",
anova_row_labels[i]);
The memory associated with anova_row_labels can be freed with a single call to free(anova_row_labels).
IMSLS_ANOVA_ROW_LABELS_USER,
char
*anova_row_labels[] (Output) Storage for the anova_row_labels,
provided by the user. The amount of space required will vary depending
upon the number of factors and n_anova.
An upperbound on the required memory is
char *anova_row_labels[n_anova* 60].
Description
The function imsls_f_crd_factorial analyzes factorial experiments replicated in different locations. Unequal replication for each treatment and missing observations are allowed. All factors are regarded as fixed effects in the analysis. However, if multiple locations appear in the data, i.e., n_locations > 1, then all effects involving locations are treated as random effects.
If n_locations = 1, then the residual mean square is used as the error mean square in calculating the F-tests for all other effects. That is
 , when n_locations = 1.
, when n_locations = 1.
If n_locations > 1 then the error mean squares for all factor F-tests is the pooled location interaction. For example, if n_factors = 2 then the error sum of squares, degrees of freedom and mean squares are calculated by:

Example
The following example is based upon data from a 3x2x2 completely randomized design conducted at one location. For demonstration purposes, observation 9 is set to missing.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "imsls.h"
void ex_crd_doc(){
int n_obs = 12;
int n_locations = 1;
int n_factors = 3;
int n_levels[4] ={3, 2, 2, 1};
int page_width = 132;
/* model information */
int model[]={
1, 1, 1, 1,
1, 1, 1, 2,
1, 1, 2, 1,
1, 1, 2, 2,
1, 2, 1, 1,
1, 2, 1, 2,
1, 2, 2, 1,
1, 2, 2, 2,
1, 3, 1, 1,
1, 3, 1, 2,
1, 3, 2, 1,
1, 3, 2, 2
};
/* response data */
float y[] ={
4.42725419998168950,
2.12795543670654300,
2.55254390835762020,
1.21479606628417970,
2.47588264942169190,
5.01306104660034180,
4.73502767086029050,
4.58392113447189330,
5.01421167794615030,
4.11972457170486450,
6.51671624183654790,
4.73365202546119690
};
int model_order;
int i, j, k, l, m, n_missing, i2, j2;
int n_factor_levels=0, n_treatments=1;
int n_two_way_means=0, n_two_way_std_err=0;
int n_two_way_interactions=0;
int n_subscripts, n_anova_table=2;
float cv, grand_mean;
float *anova_table;
float *two_way_means, *two_way_std_err;
float *treatment_means, *treatment_std_err;
float *factor_means;
float *factor_std_err;
float aNaN = imsls_f_machine(6);
char **anova_row_labels;
char *col_labels[] = {" ", "\nID", "\nDF", "\nSSQ ",
"Mean \nsquares", "\nF-Test", "\np-Value"};
/*
* Compute the length of some of the output arrays.
*/
model_order = n_factors-1;
for (i=0; i < n_factors; i++){
n_factor_levels = n_factor_levels + n_levels[i];
n_treatments = n_treatments*n_levels[i];
for (j=i+1; j < n_factors; j++){
n_two_way_interactions++;
}
}
n_two_way_std_err = n_two_way_interactions;
for (i=0; i < n_factors-1; i++){
for (j=i+1; j < n_factors; j++){
n_two_way_means = n_two_way_means + n_levels[i]*n_levels[j];
}
}
n_subscripts = n_factors;
n_anova_table = 2;
for (i=1; i <= model_order; i++){
n_anova_table += (int)imsls_f_binomial_coefficient(n_subscripts, i);
}
/* Set observation 9 to missing. */
y[8] = aNaN;
anova_table = imsls_f_crd_factorial(n_obs, n_locations, n_factors,
n_levels, model, y,
IMSLS_N_MISSING, &n_missing,
IMSLS_CV, &cv,
IMSLS_GRAND_MEAN, &grand_mean,
IMSLS_FACTOR_MEANS, &factor_means,
IMSLS_FACTOR_STD_ERRORS, &factor_std_err,
IMSLS_TWO_WAY_MEANS, &two_way_means,
IMSLS_TWO_WAY_STD_ERRORS, &two_way_std_err,
IMSLS_TREATMENT_MEANS, &treatment_means,
IMSLS_TREATMENT_STD_ERROR, &treatment_std_err,
IMSLS_ANOVA_ROW_LABELS, &anova_row_labels,
0) ;
/* Output results. */
imsls_page(IMSLS_SET_PAGE_WIDTH, &page_width);
/* Print ANOVA table. */
imsls_f_write_matrix(" *** ANALYSIS OF VARIANCE TABLE ***",
n_anova_table, 6, anova_table,
IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.3f%8.3f%8.3f%8.3f",
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_COL_LABELS, col_labels,
0);
printf("\n\nNumber of Missing Values Estimated: %d", n_missing);
printf("\nGrand Mean: %7.3f", grand_mean);
printf("\nCoefficient of Variation: %7.3f", cv);
m=0;
/* Print Factor Means. */
printf("\n\nFactor Means\n");
for(i=0; i < n_factors; i++){
printf(" Factor %d: ", i+1);
for(j=0; j < n_levels[i]; j++){
printf(" %f ", factor_means[m]);
m++;
}
k = (int)factor_std_err[2*i+1];
printf("\n std. err.(df): %f(%d) \n",
factor_std_err[2*i], k);
}
/* Print Two-Way Means. */
printf("\n\nTwo-Way Means");
m = 0;
l=0;
for(i=0; i < n_factors-1; i++){
for(j=i+1; j < n_factors; j++){
printf("\n Factor %d by Factor %d: \n", i+1, j+1);
for(i2=0; i2 < n_levels[i]; i2++){
for(j2=0; j2 < n_levels[j]; j2++){
printf(" %f ",two_way_means[m]);
m++;
}
printf("\n");
}
k = (int)two_way_std_err[l+1];
printf(" std. err.(df): = %f(%d) \n", two_way_std_err[l], k);
l+=2;
}
}
/* Print Treatment Means. */
printf("\n\nTreatment Means\n");
m = 0;
for(i=0; i < n_levels[0]; i++){
for(j=0; j < n_levels[1]; j++){
for(k=0; k < n_levels[2]; k++){
printf(" Treatment[%d][%d][%d] Mean: %f \n",
i+1, j+1, k+1, treatment_means[m]);
m++;
}
}
}
k = (int)treatment_std_err[1];
printf("\n Treatment Std. Err (df) %f(%d) \n",
treatment_std_err[0], k);
}
Output
*** ANALYSIS OF VARIANCE TABLE ***
Mean
ID DF SSQ squares F-Test p-Value
[1] -1 2 13.060 6.530 7.843 0.245
[2] -1 1 0.107 0.107 0.129 0.780
[3] -1 1 1.301 1.301 1.563 0.429
[1]x[2] -2 2 3.768 1.884 2.263 0.425
[1]x[3] -2 2 5.253 2.626 3.154 0.370
[2]x[3] -2 1 0.560 0.560 0.672 0.563
Residual -4 1 1.665 1.665 ........ ........
Total -5 10 25.715 ........ ........ ........
Number of Missing Values Estimated: 1
Grand Mean: 3.961
Coefficient of Variation: 32.574
Factor Means
Factor 1: 2.580637 4.201973 5.101885
std. err.(df): 0.912459(1)
Factor 2: 3.866888 4.056109
std. err.(df): 0.745020(1)
Factor 3: 4.290812 3.632185
std. err.(df): 0.745020(1)
Two-Way Means
Factor 1 by Factor 2:
3.277605 1.883670
3.744472 4.659474
4.578587 5.625184
std. err.(df): = 1.290412(1)
Factor 1 by Factor 3:
3.489899 1.671376
3.605455 4.798491
5.777082 4.426688
std. err.(df): = 1.290412(1)
Factor 2 by Factor 3:
3.980195 3.753580
4.601429 3.510790
std. err.(df): = 1.053617(1)
Treatment Means
Treatment[1][1][1] Mean: 4.427254
Treatment[1][1][2] Mean: 2.127955
Treatment[1][2][1] Mean: 2.552544
Treatment[1][2][2] Mean: 1.214796
Treatment[2][1][1] Mean: 2.475883
Treatment[2][1][2] Mean: 5.013061
Treatment[2][2][1] Mean: 4.735028
Treatment[2][2][2] Mean: 4.583921
Treatment[3][1][1] Mean: 5.037448
Treatment[3][1][2] Mean: 4.119725
Treatment[3][2][1] Mean: 6.516716
Treatment[3][2][2] Mean: 4.733652
Treatment Std. Err (df) 1.824919(1)
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |