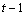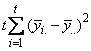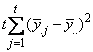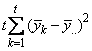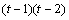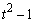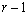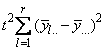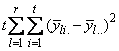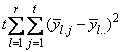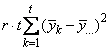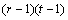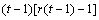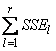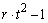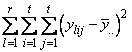Analyzes data from latin-square experiments. Function latin_square also analyzes latin-square experiments replicated at several locations.
Synopsis
#include <imsls.h>
float *
imsls_f_latin_square (int
n,
int n_locations,
int n_treatments, int
row[],
int col[], int
treatment[],
float y[], …, 0)
The type double function is imsls_d_latin_square.
Required Arguments
int n
(Input)
Number of missing and non-missing experimental observations.
imsls_f_latin_square
verifies that:
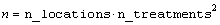
hint n_locations
(Input)
Number of locations. n_locations must be
one or greater. If n_locations>1 then
the optional array locations[] must be
included as input to imsls_f_latin_square.
int n_treatments
(Input)
Number of treatments. n_treatments must be
greater than one. In addition the number of rows and columns must be equal
to n_treatments.
int row[]
(Input)
An array of length n containing the row
identifiers for each observation in y. Each row must
be assigned values from 1 to n_treatments.
imsls_f_latin_square
verifies that the number of unique factor A identifiers is equal to n_treatments.
int
col[]
(Input)
An array of length n containing the
column identifiers for each observation in y. Each column
must be assigned values from 1 to n_treatments.
imsls_f_latin_square
verifies that the number of unique column identifiers is equal to n_treatments.
int treatment[]
(Input)
An array of length n containing the
treatment identifiers for each observation in y. Each
treatment must be assigned values from 1 to n_treatments.
imsls_f_latin_square
verifies that the number of unique treatment identifiers is equal to n_treatments.
float y[] (Input)
An
array of length n containing the
experimental observations and any missing values. Missing values cannot be
omitted. They are indicated by placing a NaN (not a number) in y. The NaN value can be
set using either the function imsls_f_machine(6) or
imsls_d_machine((6),
depending upon whether single or double precision is being used,
respectively. The location, row, column, and treatment number for each
observation in y
are identified by the corresponding values in the arguments locations, row, col, and treatment.
Return Value
Address of a pointer to the memory location of a two
dimensional, 7 by 6 array containing the ANOVA table. Each row in this
array contains values for one of the effects in the ANOVA table. The first
value in each row,
anova_tablei,0
=
anova_table[i*6],
identifies the source for the effect associated with values in that row.
The remaining values in a row contain the ANOVA table values using the following
convention:
|
J |
anova_tablei,j = anova_table[i*6+j] |
|
0 |
Source Identifier (values described below) |
|
1 |
Degrees of freedom |
|
2 |
Sum of squares |
|
3 |
Mean squares |
|
4 |
F-statistic |
|
5 |
p-value for this F-statistic |
The Source Identifiers in the first column of anova_tablei,j are the only negative values in anova_table[]. Assignments of identifiers to ANOVA sources use the following coding:
|
Source Identifier |
ANOVA Source |
|
-1 |
LOCATIONS † |
|
-2 |
ROWS |
|
-3 |
COLUMNS |
|
-4 |
TREATMENTS |
|
-5 |
LOCATIONS × TREATMENTS † |
|
-6 |
ERROR WITHIN LOCATIONS |
|
-7 |
CORRECTED TOTAL |
Notes: † If n_locations=1 rows involving location are set to missing (NaN).
Synopsis with Optional Arguments
#include <imsl.h>
float *
imsls_f_latin_square (int n, int n_locations, int n_treatments, int row[], int
col[], int treatment[], float y[],
IMSLS_RETURN_USER,
float anova_table[],
IMSLS_LOCATIONS, int
locations[],
IMSLS_N_MISSING, int *n_missing,
IMSLS_CV,
float *cv,
IMSLS_GRAND_MEAN, float
*grand_mean,
IMSLS_TREATMENT_MEANS, float
**treatment_means,
IMSLS_TREATMENT_MEANS_USER, float
treatment_means[],
IMSLS_STD_ERRORS, float
**std_err,
IMSLS_STD_ERRORS_USER, float
std_err[],
IMSLS_LOCATION_ANOVA_TABLE float
**location_anova_table,
IMSLS_LOCATION_ANOVA_TABLE_USER,
float location_anova_table[],
IMSLS_ANOVA_ROW_LABELS,
char ***anova_row_labels,
IMSLS_ANOVA_ROW_LABELS_USER, char
*anova_row_labels[],
0)
Optional Arguments
IMSLS_RETURN_USER,
float anova_table[]
(Output)
User defined array of length 42 for storage of the 7 by 6 anova
table described as the return argument for this routine. For a detailed
description of the format for this table, see the previous description of the
return arguments for imsls_f_latin_square.
IMSLS_LOCATIONS,
int locations[]
(Input)
An array of length n containing the
location identifiers for each observation in y. Unique
integers must be assigned to each location in the study. This argument is
required when n_locations>1.
IMSLS_N_MISSING,
int *n_missing
(Output)
Number of missing values, if any, found in y. Missing
values are denoted with a NaN (Not a Number) value.
IMSLS_CV, float
*cv
(Output)
The coefficient of variation computed by using the within
location standard deviation.
IMSLS_GRAND_MEAN,
float *grand_mean
(Output)
Mean of all the data across every location.
IMSLS_TREATMENT_MEANS,
float **treatment_means
(Output)
Address of a pointer to an internally allocated array of
size n_treatments
containing the treatment means.
IMSLS_TREATMENT_MEANS_USER,
float treatment_means[]
(Output)
Storage for the array treatment_means,
provided by the user.
IMSLS_STD_ERRORS,
float **std_err
(Output)
Address of a pointer to an internally allocated array
of length 2 containing the standard error and associated degrees of
freedom for comparing two treatment means. std_err[0] contains the
standard error and its degrees of freedom are returned in std_err[1].
IMSLS_STD_ERRORS_USER,
float std_err[]
(Output)
Storage for the array std_err, provided by
the user.
IMSLS_LOCATION_ANOVA_TABLE,
float **location_anova_table
(Output)
Address of a pointer to an internally allocated
3-dimensional array of size n_locations by 7 by 6
containing the anova tables associated with each location. For each
location, the 7 by 6 dimensional array corresponds to the anova table for that
location. For example, location_anova_table[(i-1)×42+(j-1)×6 + (k-1)] contains the value
in the kth column and jth row of the anova-table for the
ith location.
IMSLS_LOCATION_ANOVA_TABLE_USER, float anova_table[] (Output)
Storage for the array location_anova_table, provided by the user.
IMSLS_ANOVA_ROW_LABELS,
char ***anova_row_labels
(Output)
Address of a pointer to a pointer to an internally allocated array
containing the labels for each of the n_anova rows of the
returned ANOVA table. The label for the ith row of the ANOVA table
can be printed with printf("%s", anova_row_labels[i]).
The memory associated with anova_row_labels can be freed with a single call to free(anova_row_labels).
IMSLS_ANOVA_ROW_LABELS_USER,
char *anova_row_labels[]
(Output)
Storage for the array anova_row_labels,
provided by the user. The amount of space required will vary depending
upon the number of factors and n_anova. An
upperbound on the required memory is
char *anova_row_labels[600].
Description
The function imsls_f_latin_square analyzes latin-square experiments, possibly replicated at multiple locations. Latin-square experiments block treatments using two factors: rows and columns. The number of levels associated with rows and columns must equal the number of treatments. Treatments are blocked by rows and columns in a balanced arrangement to ensure that every row contain one replicate of every treatment. The same balance is required for every column, see Table 1. Notice that the four treatments, T1, T2, T3, and T4, appear exactly once in every column and every row.
|
|
|
Columns | |||
|
|
|
C1 |
C2 |
C3 |
C4 |
|
|
R1 |
T1 |
T2 |
T3 |
T4 |
|
R2 |
T2 |
T3 |
T4 |
T1 | |
|
R3 |
T3 |
T4 |
T1 |
T2 | |
|
R4 |
T4 |
T1 |
T2 |
T3 | |
Table 1 Latin-Square Experiment with Four Treatments
A necessary assumption in Latin-Square experiments is that there are no interactions between treatments and the row and column blocking factors. For data collected at a single location, the Anova table for a Latin-Square experiment is usually organized into five rows, see Table 2.
|
SOURCE |
DF |
Sum of Squares |
Mean Squares |
|
ROWS |
|
SSR= |
MSR |
|
COLUMNS |
|
SSC= |
MSC |
|
TREATMENTS |
|
SST= |
MST |
|
ERROR |
|
SSE=SSTot-SSR-SSC-SST |
MSE |
|
TOTAL |
|
SSTot= | |
Table 2 – The ANOVA Table for a Latin-Square Experiment at one Location
The statistical model used to represent data is from a single location:
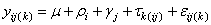 ,
,
where
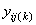 is
the observation for the kth treatment in the ith row and
jth column of the Latin Square, and,
is
the observation for the kth treatment in the ith row and
jth column of the Latin Square, and,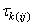 is the effect associated with the
kth treatment.
is the effect associated with the
kth treatment.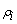 and
and
 are the ith row
and jth column effects, respectively, and
are the ith row
and jth column effects, respectively, and 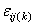 is the noise associated with this
observation.
is the noise associated with this
observation.
If multiple locations are involved, imsls_f_latin_square assumes that treatments are crossed with locations, but that row and column effects are nested within locations, see Table 3. The statistical model used to represent these data is:
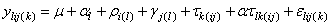 ,
,
where
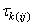
is the effect associated with the kth treatment, and
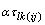
is the interaction effect between location l and treatment k.
|
SOURCE |
DF |
Sum of Squares |
Mean Squares |
|
LOCATIONS |
|
SSL= |
MSL |
|
ROWS |
|
SSR= |
MSR |
|
COLUMNS |
|
SSC= |
MSC |
|
TREATMENTS |
|
SST= |
MST |
|
LOCATIONS X TREATMENTS |
|
SSLT by difference |
MSLT |
|
ERROR |
|
SSE= |
MSE |
|
TOTAL |
|
SSTot= |
|
Table 3 – The ANOVA Table for a Latin-Square Experiment at Multiple Locations
Example
This example uses four treatments organized into a latin square. This example also uses the function l_print_LSD(), which is defined in the first example for imsls_f_lattice().
#include <stdio.h>
#include <math.h>
#include "imsls.h"
void l_print_LSD(int n1, int* equalMeans, float *means);
void main()
{
char **anova_row_labels;
char *col_labels[] = {" ", "\nID", "\nDF", "\nSSQ ",
"Mean \nsquares", "\nF-Test", "\np-Value"};
float alpha = 0.05;
int i, l, page_width = 132;
int n = 16; /* Total number of observations */
int n_locations = 1; /* Number of locations */
int n_treatments = 4; /* Number of rows, columns and treatments */
int n_aov_rows = 7; /* Number of rows in the latin-square anova table */
int col[]={1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4};
int row[]={3, 2, 4, 1, 1, 4, 2, 3, 2, 3, 1, 4, 4, 1, 3, 2};
int treatment[]={1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4};
float y[]={
1.167, 1.185, 1.655, 1.345, 1.64, 1.29, 1.665, 1.29,
1.475, 0.71, 1.425, 0.66, 1.565, 1.29, 1.4, 1.18};
float grand_mean;
float cv;
float *aov;
float *treatment_means;
float *std_err;
int df;
int *equal_means;
printf("\n\n*** Experimental Design ***");
printf("\n===============================");
printf("\n| COL | 1 | 2 | 3 | 4 |");
printf("\n===============================");
printf("\n|ROW 1 | 2 | 4 | 3 | 1 |");
printf("\n===============================");
printf("\n|ROW 2 | 3 | 1 | 2 | 4 |");
printf("\n===============================");
printf("\n|ROW 3 | 1 | 3 | 4 | 2 |");
printf("\n===============================");
printf("\n|ROW 4 | 4 | 2 | 1 | 3 |");
printf("\n===============================");
aov = imsls_f_latin_square(n, n_locations, n_treatments, row, col,
treatment, y,
IMSLS_GRAND_MEAN, &grand_mean,
IMSLS_CV, &cv,
IMSLS_TREATMENT_MEANS, &treatment_means,
IMSLS_STD_ERRORS, &std_err,
IMSLS_ANOVA_ROW_LABELS, &anova_row_labels,
0);
/* Output results. */
imsls_page(IMSLS_SET_PAGE_WIDTH, &page_width);
/* Print ANOVA table. */
imsls_f_write_matrix("\n *** ANALYSIS OF VARIANCE TABLE ***",
7, 6, aov,
IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.3f%8.3f%8.3f%8.3f",
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_COL_LABELS, col_labels,
0);
printf("\n\nGrand Mean: %7.3f", grand_mean);
printf("\n\nCoefficient of Variation: %7.3f\n\n", cv);
l = 0;
printf("Treatment Means: \n");
for (i=0; i < n_treatments; i++){
printf("treatment[%2d] %7.4f \n", i+1, treatment_means[l++]);
}
df = (int)std_err[1];
printf("\n\nStandard Error for Comparing Two Treatment Means: %f \n(df=%d)\n",
std_err[0], df);
equal_means = imsls_f_multiple_comparisons(n_treatments, treatment_means, df,
std_err[0]/sqrt(2.0),
IMSLS_LSD,
IMSLS_ALPHA, alpha,
0);
l_print_LSD(n_treatments, equal_means, treatment_means);
}
Output
*** Experimental Design ***
===============================
| COL | 1 | 2 | 3 | 4 |
===============================
|ROW 1 | 2 | 4 | 3 | 1 |
===============================
|ROW 2 | 3 | 1 | 2 | 4 |
===============================
|ROW 3 | 1 | 3 | 4 | 2 |
===============================
|ROW 4 | 4 | 2 | 1 | 3 |
===============================
*** ANALYSIS OF VARIANCE TABLE ***
Mean
ID DF SSQ squares F-Test p-Value
Locations ................. -1 ... ........ ........ ........ ........
Rows within Locations ..... -2 3 0.185 0.062 2.064 0.207
Columns within Locations .. -3 3 0.589 0.196 6.579 0.025
Treatments ................ -4 3 0.352 0.117 3.927 0.073
Locations x Treatments .... -5 ... ........ ........ ........ ........
Error within Locations .... -6 6 0.179 0.030 ........ ........
Corrected Total ........... -7 15 1.305 ........ ........ ........
Grand Mean: 1.309
Coefficient of Variation: 13.204
Treatment Means:
treatment[ 1] 1.3380
treatment[ 2] 1.4712
treatment[ 3] 1.0675
treatment[ 4] 1.3587
Standard Error for Comparing Two Treatment Means: 0.122202
(df=6)
[group] Mean LSD Grouping
[3] 1.067500 *
[1] 1.338000 * *
[4] 1.358750 * *
[2] 1.471250 *
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |