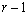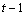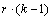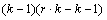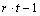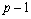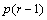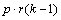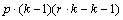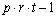Analyzes balanced and partially-balanced lattice experiments. In these experiments, a requirement is that the number of treatments be equal to the square of an integer, such as 9, 16, or 25 treatments. Function lattice also analyzes repetitions of lattice experiments.
Synopsis
#include <imsls.h>
float *
imsls_f_lattice
(int n, int
n_locations,
int n_reps,
int
n_blocks,
int n_treatments, int
rep[],
int block[],
int
treatment[],
float y[],…, 0)
The type double function is imsls_d_lattice.
Required Arguments
int n
(Input)
Number of missing and non-missing experimental
observations. imsls_f_balanced_lattice
verifies that:
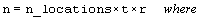
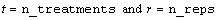 .
.
int n_locations
(Input)
Number of locations or repetitions of the lattice
experiments. n_locations must be
one or greater. If n_locations>1 then
the optional arguments IMSLS_LOCATIONS must
be included as input to imsls_f_lattice.
int n_reps
(Input)
Number of replicates per location. Each replicate
should consist of
t = n_treatments organized
into  blocks.
blocks.
int n_blocks
(Input)
Number of blocks per location. For every location,
n_blocks must be
equal to n_blocks=
r·k, where r = n_reps and
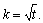
int n_treatments
(Input)
Number of treatments t = n_treatments must be
equal to k2.
int rep[]
(Input)
An array of length n containing the
replicate identifiers for each observation in y. For a
balanced-lattice, the number of replicate identifiers must be equal to n_reps=(k+1). For a partially-balanced
lattice, the number of replicate identifiers depends upon whether the design is
a simple lattice, triple lattice, etc. imsls_f_lattice
verifies that the number of unique replicate identifiers is equal to n_reps. If
multiple locations or repetitions of the experiment is conducted, i.e., n_locations>1, then
the replicate and block numbers contained in rep and block must agree
between repetitions.
int block[]
(Input)
An array of length n containing the block
identifiers for each observation in y. imsls_f_lattice
verifies that the number of unique block identifiers is equal to n_blocks. If
multiple locations or repetitions of the experiment is conducted, i.e., n_locations>1, then
block numbers must agree between repetitions. That is, the ith
block in every location or repetition must contain the same treatments.
int treatment[]
(Input)
An array of length n containing the
treatment identifiers for each observation in y. Each
treatment must be assigned values from 1 to n_treatments.
imsls_f_lattice
verifies that the number of unique treatment identifiers is equal to n_treatments.
float y[] (Input)
An
array of length n containing the
experimental observations and any missing values. Missing values cannot be
omitted. They are indicated by placing a NaN (not a number) in y. The NaN value can
be set using either the function imsls_f_machine(6) or imsls_d_machine(6), depending upon
whether single or double precision is being used, respectively. The
location, replicate, block, and treatment number for each observation in y are identified by
the corresponding values in the arguments locations, rep, block, and treatment.
Return Value
Address of a pointer to the memory location of a two
dimensional, 7 by 6 array containing the ANOVA table. Each row in this
array contains values for one of the effects in the ANOVA table. The first
value in each row,
anova_tablei,0
=
anova_table[i*6],
identifies the source for the effect associated with values in that row.
The remaining values in a row contain the ANOVA table values using the following
convention:
|
J |
anova_tablei,j = anova_table[i*6+j] |
|
0 |
Source Identifier (values described below) |
|
1 |
Degrees of freedom |
|
2 |
Sum of squares |
|
3 |
Mean squares |
|
4 |
F-statistic |
|
5 |
p-value for this F-statistic |
The Source Identifiers in the first column of anova_tablei,j are the only negative values in anova_table[]. Assignments of identifiers to ANOVA sources use the following coding:
|
Source Identifier |
ANOVA Source |
|
-1 |
LOCATIONS † |
|
-2 |
REPLICATES |
|
-3 |
TREATMENTS(unadjusted) |
|
-4 |
TREATMENTS(adjusted) |
|
-5 |
BLOCKS(adjusted) |
|
-6 |
INTRA-BLOCK ERROR |
|
-7 |
CORRECTED TOTAL |
Notes: † If n_locations=1, all entries in this row are set to missing (NaN).
Synopsis with Optional Arguments
#include <imsl.h>
float
*
imsls_f_lattice(int
n,
int n_locations, int
n_reps,
int n_blocks, int
n_treatments, int
rep[],
int block[],
int
treatment[], float
y[],
IMSLS_RETURN_USER, float
anova_table[]
IMSLS_LOCATIONS, int
locations[],
IMSLS_N_MISSING, int
*n_missing,
IMSLS_CV, float
*cv,
IMSLS_GRAND_MEAN, float
*grand_mean,
IMSLS_TREATMENT_MEANS, float
**treatment_means,
IMSLS_TREATMENT_MEANS_USER, float
treatment_means[],
IMSLS_STD_ERRORS, float
**std_err,
IMSLS_STD_ERRORS_USER, float
std_err[],
IMSLS_LOCATION_ANOVA_TABLE float
**location_anova_table,
IMSLS_LOCATION_ANOVA_TABLE_USER,
float
location_anova_table[],
IMSLS_ANOVA_ROW_LABELS, char
***anova_row_labels,
IMSLS_ANOVA_ROW_LABELS_USER, char
*anova_row_labels[],
0)
Optional Arguments
IMSLS_RETURN_USER,
float anova_table[]
(Output)
User defined array of length 42 for storage of the 7 by 6 anova
table described as the return argument for imsls_f_lattice.
For a detailed description of the format for this table, see the previous
description of the return arguments for imsls_d_lattice.
IMSLS_LOCATIONS,
int locations[]
(Input)
An array of length n containing the
location or repetition identifiers for each observation in y. Unique
integers must be assigned to each location in the study. This argument is
required when n_locations>1.
IMSLS_N_MISSING,
int *n_missing
(Output)
Number of missing values, if any, found in y. Missing
values are denoted with a NaN (Not a Number) value.
IMSLS_CV, float
*cv
(Output)
The coefficient of variation computed by using the
location standard deviation.
IMSLS_GRAND_MEAN,
float
*grand_mean (Output)
The overall adjusted mean averaged over
every location.
IMSLS_TREATMENT_MEANS,
float **treatment_means
(Output)
Address of a pointer to an internally allocated array of
size n_treatments
containing the adjusted treatment means.
IMSLS_TREATMENT_MEANS_USER,
float
treatment_means[] (Output)
Storage for the array treatment_means,
provided by the user.
IMSLS_STD_ERRORS,
float **std_err
(Output)
Address of a pointer to an internally allocated array
of length 4 containing the standard error and associated degrees of
freedom for comparing two treatment means. std_err[0] contains
the standard error for comparing two treatments that appear in the same block at
least once. std_err[1] contains
the standard error for comparing two treatments that never appear in the same
block together. std_err[2] contains
the standard error for comparing, on average, two treatments from the experiment
averaged over cases in which the treatments do or do not appear in the same
block. Finally, std_err[3]
contains the degrees of freedom associated with each of these standard
errors, i.e., std_err[3]= degrees of
freedom for intra-block error.
IMSLS_STD_ERRORS_USER,
float std_err[]
(Output)
Storage for the array std_err, provided by
the user.
IMSLS_LOCATION_ANOVA_TABLE,
float **location_anova_table
(Output)
Address of a pointer to an internally allocated 3-dimensional array
of size n_locations by 7
by 6 containing the anova tables associated with each location or repetition of
the lattice experiment. For each location, the 7 by 6 dimensional array
corresponds to the anova table for that location.
For example, location_anova_table[(i-1)×42+(j-1)×6
+ (k-1)] contains the value in the
kth column and jth row of the anova-table for the ith
location.
IMSLS_LOCATION_ANOVA_TABLE_USER,
float anova_table[]
(Output)
Storage for the array location_anova_table,
provided by the user.
IMSLS_ANOVA_ROW_LABELS,
char ***anova_row_labels
(Output)
Address of a pointer to a pointer to an internally allocated array
containing the labels for each of the n_anova rows of the
returned ANOVA table. The label for the ith row of the ANOVA table can be
printed with printf("%s",
anova_row_labels[i]);
The memory associated with anova_row_labels
can be freed with a single call to free(anova_row_labels).
IMSLS_ANOVA_ROW_LABELS_USER,
char *anova_row_labels[]
(Output)
Storage for the array anova_row_labels,
provided by the user. The amount of space required will vary depending
upon the number of factors and n_anova. An upperbound
on the required memory is
char *anova_row_labels[600];
Description
The function imsls_f_lattice analyzes both balanced and partially-balanced lattice experiments, possibly repeated at multiple locations. These designs were originally described by Yates (1936). A defining characteristic of these classes of lattice experiments is that the number of treatments is always the square of an integer, such as t=9, 16, 25, etc. where t is equal to the number of treatments.
Another characteristic of lattice experiments is that
blocks are organized into replicates, where each replicate contains one
observation for each treatment. This requires the number of blocks
in each replicate to be equal to the number of observations per block.
That is, the number of blocks per replicate and the number of observations per
block are both equal to  .
.
For balanced lattice
experiments the number of replicates is always 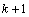 . For
partially-balanced lattice experiments, the number of replicates is less than
. For
partially-balanced lattice experiments, the number of replicates is less than
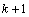 . Tables of balanced-lattice experiments are tabulated
in Cochran & Cox (1950) for t=9, 16, 25, 49, 64 and 81.
. Tables of balanced-lattice experiments are tabulated
in Cochran & Cox (1950) for t=9, 16, 25, 49, 64 and 81.
The analysis of balanced and partially-balanced experiments is detailed in Cochran & Cox (1950) and Kuehl (2000).
Consider, for example, a 3x3 balanced-lattice, i.e., k=3 and t=9. Notice that the number of replicates is 4 and the number of blocks per replicate is equal to 3. The total number of blocks is equal to
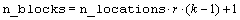 .
.
For a balanced-lattice,
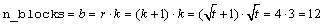 .
.
|
Replicate I |
Replicate II |
|
Block 1 (T1, T2, T3) |
Block 4 (T1, T4, T7) |
|
Block 2 (T4, T5, T6) |
Block 5 (T2, T5, T8) |
|
Block 3 (T7, T8, T9) |
Block 6 (T3, T6, T9) |
|
Replicate III |
Replicate IV |
|
Block 7 (T1, T5, T9) |
Block 10 (T1, T6, T8) |
|
Block 8 (T2, T6, T7) |
Block 11 (T2, T4, T9) |
|
Block 9 (T3, T4, T8) |
Block 12 (T3, T5, T7) |
Table 4- 1 A 3x3 Balanced-Lattice for 9 Treatments in Four Replicates.
The analysis of variance for data from a balanced-lattice experiment, takes the form familiar to other balanced incomplete block experiments. In these experiments, the error term is divided into two components: the Inter-Block Error and the Intra-Block Error. For single and multiple locations, the general format of the anova tables is illustrated in the Tables 2 and 3.
|
SOURCE |
DF |
Sum of Squares |
Mean Squares |
|
REPLICATES |
|
SSR |
MSR |
|
TREATMENTS(unadj) |
|
SST |
MST |
|
TREATMENTS(adj) |
|
SSTa |
MSTa |
|
BLOCKS(adj) |
|
SSBa |
MSBa |
|
INTRA-BLOCK ERROR |
|
SSI |
MSI |
|
TOTAL |
|
SSTot | |
Table 4- 2 The ANOVA Table for a Lattice Experiment at one Location
|
SOURCE |
DF |
Sum of Squares |
Mean Squares |
|
LOCATIONS |
|
SSL |
MSL |
|
REPLICATES WITHIN LOCATIONS |
|
SSR |
MSR |
|
TREATMENTS(unadj) |
|
SST |
MST |
|
TREATMENTS(adj) |
|
SSTa |
MSTa |
|
BLOCKS(adj) |
|
SSB |
MSB |
|
INTRA-BLOCK ERROR |
|
SSI |
MSI |
|
TOTAL |
|
SSTot | |
Table 4- 3 The ANOVA Table for a Lattice Experiment at Multiple Locations
Example 1
This example is a lattice design for 16 treatments conducted at one location. A lattice design with t=k2=16 treatments is a balanced lattice design with r= k+1=5 replicates and r·k=5(4)=20 blocks.
#include <stdlib.h>
#include <math.h>
#include "imsls.h"
void l_print_LSD(int n1, int* equalMeans, float *means);
void main()
{
char **anova_row_labels = NULL;
char *col_labels[] = {" ", "\nID", "\nDF", "\nSSQ ",
"Mean \nsquares", "\nF-Test", "\np-Value"};
float alpha = 0.05;
int i, l, page_width = 132;
int n = 80; /* Total number of observations */
int n_locations = 1; /* Number of locations */
int n_treatments =16; /* Number of treatments */
int n_reps = 5; /* Number of replicates */
int n_blocks =20; /* Total number of blocks */
int n_aov_rows = 7; /* Number of rows in the anova table */
int rep[]={
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5
};
int block[]={
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4,
5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8,
9, 9, 9, 9, 10, 10, 10, 10, 11, 11, 11, 11, 12, 12, 12, 12,
13, 13, 13, 13, 14, 14, 14, 14, 15, 15, 15, 15, 16, 16, 16, 16,
17, 17, 17, 17, 18, 18, 18, 18, 19, 19, 19, 19, 20, 20, 20, 20
};
int treatment[]={
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
1, 5, 9, 13, 10, 2, 14, 6, 7, 15, 3, 11, 16, 8, 12, 4,
1, 6, 11, 16, 5, 2, 15, 12, 9, 14, 3, 8, 13, 10, 7, 4,
1, 14, 7, 12, 13, 2, 11, 8, 5, 10, 3, 16, 9, 6, 15, 4,
1, 10, 15, 8, 9, 2, 7, 16, 13, 6, 3, 12, 5, 14, 11, 4
};
float y[] ={
147, 152, 167, 150, 127, 155, 162, 172,
147, 100, 192, 177, 155, 195, 192, 205,
140, 165, 182, 152, 97, 155, 192, 142,
155, 182, 192, 192, 182, 207, 232, 162,
155, 132, 177, 152, 182, 130, 177, 165,
137, 185, 152, 152, 185, 122, 182, 192,
220, 202, 175, 205, 205, 152, 180, 187,
165, 150, 200, 160, 155, 177, 185, 172,
147, 112, 177, 147, 180, 205, 190, 167,
172, 212, 197, 192, 177, 220, 205, 225
};
float grand_mean;
float cv;
float *aov;
float *treatment_means;
float *std_err;
int *equal_means;
int df;
aov = imsls_f_lattice(n, n_locations, n_reps, n_blocks,
n_treatments, rep, block, treatment, y,
IMSLS_GRAND_MEAN, &grand_mean,
IMSLS_CV, &cv,
IMSLS_TREATMENT_MEANS, &treatment_means,
IMSLS_STD_ERRORS, &std_err,
IMSLS_ANOVA_ROW_LABELS, &anova_row_labels,
0);
imsls_page(IMSLS_SET_PAGE_WIDTH, &page_width);
/* Print the ANOVA table. */
imsls_f_write_matrix(" *** ANALYSIS OF VARIANCE TABLE ***",
7, 6, aov,
IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.2f%7.2f%7.2f%7.3f",
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_COL_LABELS, col_labels,
0);
printf("\n\nAdjusted Grand Mean: %7.3f", grand_mean);
printf("\n\nCoefficient of Variation: %7.3f\n\n", cv);
l = 0;
printf("Adjusted Treatment Means: \n");
for (i=0; i < n_treatments; i++){
printf("treatment[%2d] %7.4f \n", i+1, treatment_means[l++]);
}
df = (int)std_err[3];
printf("\nStandard Error for Comparing Two Adjusted Treatment Means: %f \n(df=%d)\n",
std_err[2], df);
equal_means = imsls_f_multiple_comparisons(n_treatments, treatment_means, df,
std_err[2]/sqrt(2.0),
IMSLS_LSD,
IMSLS_ALPHA, alpha,
0);
l_print_LSD(n_treatments, equal_means, treatment_means);
}
/*
* Function to display means comparison.
*/
void l_print_LSD(int n, int *equalMeans, float *means){
float x=0.0;
int i, j, k;
int iSwitch;
int *idx;
idx = (int *) malloc(n * sizeof (int));
for (k=0; k < n; k++) {
idx[k] =k+1;
}
/* Sort means in ascending order*/
iSwitch=1;
while (iSwitch != 0){
iSwitch = 0;
for (i = 0; i < n-1; i++){
if (means[i] > means[i+1]){
iSwitch = 1;
x = means[i];
means[i] = means[i+1];
means[i+1] = x;
j = idx[i];
idx[i] = idx[i+1];
idx[i+1] = j;
}
}
}
printf("[group] \t Mean \t\tLSD Grouping \n");
for (i=0; i < n; i++){
printf(" [%d] \t\t%f", idx[i], means[i]);
for (j=1; j < i+1; j++){
if(equalMeans[j-1] >= i+2-j){
printf("\t *");
}else{
if(equalMeans[j-1]>0) printf("\t");
}
}
if (i < n-1 && equalMeans[i]>0) printf("\t *");
printf("\n");
}
free(idx);
idx = NULL;
return;
}
Output
*** ANALYSIS OF VARIANCE TABLE ***
Mean
ID DF SSQ squares F-Test p-Value
Locations ................. -1 ... ........ ....... ....... .......
Replicates ................ -2 4 6524.38 1631.10 ....... .......
Treatments (unadjusted) ... -3 15 27297.13 1819.81 4.12 0.000
Treatments (adjusted) ..... -4 15 21271.29 1418.09 4.21 0.000
Blocks (adjusted) ......... -5 15 11339.28 755.95 ....... .......
Intra-Block Error ......... -6 45 15173.09 337.18 ....... .......
Corrected Total ........... -7 79 60333.88 ....... ....... .......
Adjusted Grand Mean: 171.450
Coefficient of Variation: 10.710
Adjusted Treatment Means:
treatment[ 1] 166.4533
treatment[ 2] 160.7527
treatment[ 3] 183.6289
treatment[ 4] 175.6298
treatment[ 5] 162.6806
treatment[ 6] 167.6717
treatment[ 7] 168.3821
treatment[ 8] 176.5731
treatment[ 9] 162.6928
treatment[10] 118.5197
treatment[11] 189.0615
treatment[12] 190.4607
treatment[13] 169.4514
treatment[14] 197.0827
treatment[15] 185.3560
treatment[16] 168.8029
Standard Error for Comparing Two Adjusted Treatment Means: 13.221801
(df=45)
[group] Mean LSD Grouping
[10] 118.519737
[2] 160.752731 *
[5] 162.680649 * *
[9] 162.692841 * *
[1] 166.453323 * * *
[6] 167.671661 * * *
[7] 168.382111 * * *
[16] 168.802887 * * *
[13] 169.451370 * * *
[4] 175.629776 * * * *
[8] 176.573090 * * * *
[3] 183.628906 * * * *
[15] 185.355988 * * * *
[11] 189.061508 * * *
[12] 190.460724 * *
[14] 197.082703 *
Example 2
This example consists of a 5 × 5 partially-balanced lattice repeated twice. In this case, the number of replicates is not k+1 = 6, it is only n_reps = 2. Each lattice consists of total of 50 observations which is repeated twice. The first observation in this experiment is missing.
#include <stdlib.h>
#include <math.h>
#include "imsls.h"
void l_print_LSD(int n1, int* equalMeans, float *means);
void main()
{
char **anova_row_labels = NULL;
char **loc_row_labels = NULL;
char *col_labels[] = {" ", "\nID", "\nDF", "\nSSQ ",
"Mean \nsquares", "\nF-Test", "\np-Value"};
float alpha = 0.05;
int i, l, page_width = 132;
int n = 100; /* Total number of observations */
int n_locations = 2; /* Number of locations */
int n_treatments =25; /* Number of treatments */
int n_reps = 2; /* Number of replicates/location */
int n_blocks =10; /* Total number of blocks/location */
int n_aov_rows = 7; /* Number of rows in the anova table */
int rep[]={
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2,
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
1, 1, 1, 1, 1,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2,
2, 2, 2, 2, 2
};
int block[]={
1, 1, 1, 1, 1,
2, 2, 2, 2, 2,
3, 3, 3, 3, 3,
4, 4, 4, 4, 4,
5, 5, 5, 5, 5,
6, 6, 6, 6, 6,
7, 7, 7, 7, 7,
8, 8, 8, 8, 8,
9, 9, 9, 9, 9,
10, 10, 10, 10, 10,
1, 1, 1, 1, 1,
2, 2, 2, 2, 2,
3, 3, 3, 3, 3,
4, 4, 4, 4, 4,
5, 5, 5, 5, 5,
6, 6, 6, 6, 6,
7, 7, 7, 7, 7,
8, 8, 8, 8, 8,
9, 9, 9, 9, 9,
10, 10, 10, 10, 10
};
int treatment[]={
1, 2, 3, 4, 5,
6, 7, 8, 9, 10,
11, 12, 13, 14, 15,
16, 17, 18, 19, 20,
21, 22, 23, 24, 25,
1, 6, 11, 16, 21,
2, 7, 12, 17, 22,
3, 8, 13, 18, 23,
4, 9, 14, 19, 24,
5, 10, 15, 20, 25,
1, 2, 3, 4, 5,
6, 7, 8, 9, 10,
11, 12, 13, 14, 15,
16, 17, 18, 19, 20,
21, 22, 23, 24, 25,
1, 6, 11, 16, 21,
2, 7, 12, 17, 22,
3, 8, 13, 18, 23,
4, 9, 14, 19, 24,
5, 10, 15, 20, 25
};
int location[]={
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2
};
float y[] ={
6, 7, 5, 8, 6,
16, 12, 12, 13, 8,
17, 7, 7, 9, 14,
18, 16, 13, 13, 14,
14, 15, 11, 14, 14,
24, 13, 24, 11, 8,
21, 11, 14, 11, 23,
16, 4, 12, 12, 12,
17, 10, 30, 9, 23,
15, 15, 22, 16, 19,
13, 26, 9, 13, 11,
15, 18, 22, 11, 15,
19, 10, 10, 10, 16,
21, 16, 17, 4, 17,
15, 12, 13, 20, 8,
16, 7, 20, 13, 21,
15, 10, 11, 7, 14,
7, 11, 15, 15, 16,
19, 14, 20, 6, 16,
17, 18, 20, 15, 14
};
float grand_mean;
float cv;
float *aov;
float *location_anova_table;
float *loc_anova_table;
float *treatment_means;
float *std_err;
int df;
int n_missing;
int *equal_means;
/* Set first observation to missing. */
y[0] = imsls_f_machine(6);
aov = imsls_f_lattice(n, n_locations, n_reps, n_blocks,
n_treatments, rep, block, treatment, y,
IMSLS_LOCATIONS, location,
IMSLS_GRAND_MEAN, &grand_mean,
IMSLS_CV, &cv,
IMSLS_TREATMENT_MEANS, &treatment_means,
IMSLS_STD_ERRORS, &std_err,
IMSLS_LOCATION_ANOVA_TABLE, &location_anova_table,
IMSLS_ANOVA_ROW_LABELS, &anova_row_labels,
IMSLS_N_MISSING, &n_missing,
0);
/* Output results. */
imsls_page(IMSLS_SET_PAGE_WIDTH, &page_width);
/* Print the ANOVA table. */
imsls_f_write_matrix(" *** ANALYSIS OF VARIANCE TABLE ***",
7, 6, aov,
IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.2f%7.2f%7.2f%7.3f",
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_COL_LABELS, col_labels,
0);
/* Print the location ANOVA tables. */
for (i=0; i < n_locations; i++){
printf("\n\n\t\t\t\tLOCATION %d", i+1);
imsls_f_write_matrix(" *** ANALYSIS OF VARIANCE TABLE ***",
7, 6, &(location_anova_table[i*42]),
IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.2f%7.2f%7.2f%7.3f",
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_COL_LABELS, col_labels,
0);
}
printf("\n\nAdjusted Grand Mean: %7.3f", grand_mean);
printf("\n\nCoefficient of Variation: %7.3f\n\n", cv);
l = 0;
printf("Adjusted Treatment Means: \n");
for (i=0; i < n_treatments; i++){
printf("treatment[%2d] %7.4f \n", i+1, treatment_means[l++]);
}
df = std_err[3];
printf("\nStandard Error for Comparing Two Adjusted Treatment Means: %f \n(df=%d)\n",
std_err[2], df);
equal_means = imsls_f_multiple_comparisons(n_treatments, treatment_means, df,
std_err[2]/sqrt(2),
IMSLS_LSD,
IMSLS_ALPHA, alpha,
0);
l_print_LSD(n_treatments, equal_means, treatment_means);
printf("\n\nNumber of missing observations: %d\n", n_missing);
}
Output
*** ANALYSIS OF VARIANCE TABLE ***
Mean
ID DF SSQ squares F-Test p-Value
Locations ................. -1 1 12.19 12.19 0.25 0.622
Replicates within Locations -2 2 203.99 101.99 7.44 0.001
Treatments (unadjusted) ... -3 24 795.46 33.14 0.02 1.000
Treatments (adjusted) ..... -4 24 951.20 39.63 2.89 0.006
Blocks (adjusted) ......... -5 16 770.50 48.16 3.51 0.000
Intra-Block Error ......... -6 55 753.81 13.71 ....... .......
Corrected Total ........... -7 98 2535.95 ....... ....... .......
LOCATION 1
*** ANALYSIS OF VARIANCE TABLE ***
Mean
ID DF SSQ squares F-Test p-Value
Locations ................. -1 ... ........ ....... ....... .......
Replicates within Locations -2 1 203.67 203.67 ....... .......
Treatments (unadjusted) ... -3 24 567.13 23.63 0.78 0.721
Treatments (adjusted) ..... -4 24 661.08 27.54 2.04 0.078
Blocks (adjusted) ......... -5 8 490.51 61.31 ....... .......
Intra-Block Error ......... -6 15 202.93 13.53 ....... .......
Corrected Total ........... -7 48 1464.24 ....... ....... .......
LOCATION 2
*** ANALYSIS OF VARIANCE TABLE ***
Mean
ID DF SSQ squares F-Test p-Value
Locations ................. -1 ... ........ ....... ....... .......
Replicates within Locations -2 1 0.32 0.32 ....... .......
Treatments (unadjusted) ... -3 24 622.52 25.94 1.43 0.196
Treatments (adjusted) ..... -4 24 707.51 29.48 2.83 0.018
Blocks (adjusted) ......... -5 8 269.76 33.72 ....... .......
Intra-Block Error ......... -6 16 166.92 10.43 ....... .......
Corrected Total ........... -7 49 1059.52 ....... ....... .......
Adjusted Grand Mean: 14.011
Coefficient of Variation: 26.423
Adjusted Treatment Means:
treatment[ 1] 17.1507
treatment[ 2] 19.2200
treatment[ 3] 11.1261
treatment[ 4] 14.6230
treatment[ 5] 12.6543
treatment[ 6] 11.8133
treatment[ 7] 11.9045
treatment[ 8] 11.3106
treatment[ 9] 9.5576
treatment[10] 11.5889
treatment[11] 22.1321
treatment[12] 12.7233
treatment[13] 13.1293
treatment[14] 17.8763
treatment[15] 18.6576
treatment[16] 14.6568
treatment[17] 11.4980
treatment[18] 13.1540
treatment[19] 5.4010
treatment[20] 12.9323
treatment[21] 15.4108
treatment[22] 17.0020
treatment[23] 13.9081
treatment[24] 17.6550
treatment[25] 13.1864
Standard Error for Comparing Two Adjusted Treatment Means: 4.617277
(df=55)
[group] Mean LSD Grouping
[19] 5.400988 *
[9] 9.557555 * *
[3] 11.126063 * * *
[8] 11.310598 * * *
[17] 11.497972 * * *
[10] 11.588868 * * *
[6] 11.813338 * * *
[7] 11.904538 * * *
[5] 12.654334 * * *
[12] 12.723251 * * *
[20] 12.932302 * * * *
[13] 13.129311 * * * *
[18] 13.154031 * * * *
[25] 13.186358 * * * *
[23] 13.908089 * * * *
[4] 14.623020 * * * *
[16] 14.656771 * * *
[21] 15.410829 * * *
[22] 17.002029 * * *
[1] 17.150679 * * *
[24] 17.655045 * * *
[14] 17.876268 * * *
[15] 18.657581 * * *
[2] 19.220003 * *
[11] 22.132051 *
Number of missing observations: 1
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |