Converts time series data sorted within nominal classes in decreasing chronological order to a useful format for processing by a neural network.
Synopsis
#include <imsls.h>
float*
imsls_f_time_series_class_filter (int
n_obs, int
n_lags,
int
n_classes,
int i_class[], float x[], …,0)
The type double function is imsls_d_time_series_class_filter.
Required Arguments
int n_obs
(Input)
Number of observations. The number of observations must be
greater than n_lags.
int n_lags
(Input)
The number of lags. The number of lags must be one or
greater.
int n_classes
(Input)
The number of classes associated with these data. The number of
classes must be one or greater.
int i_class[]
(Input)
An array of length n_obs. The
ith element in i_class is equal to
the class associated with the ith element of x. The classes must be
numbered from 1 to n_classes.
float x[]
(Input)
A sorted array of length n_obs. This
array is assumed to be sorted first by class designations and then descending by
chronological order, i.e., most recent observations appear first within a
class.
Return Value
A pointer to an internally allocated array of size n_obs by n_lags columns. If errors are encountered, then NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float*
imsls_f_time_series_class_filter (int
n_obs, int
n_lags,
int
n_classes, int
i_class[],
float x[],
IMSLS_RETURN_USER, float z[],
IMSLS_LAGS, int lag[],
0)
The type double function is imsls_d_time_series_class_filter.
Optional Arguments
IMSLS_RETURN_USER, float z[]
(Output)
A user-supplied array of size n_obs by n_lags. The
ith column contains the lagged values of x for a lag equal to
the number of lags in lag[i].
IMSLS_LAGS,
int
lag[] (Input)
An array of length n_lags. The
ith element in lag is equal to the
lag requested for the ith column of z. Every lag
must be non-negative.
Default: lag[i]=i
Description
The function imsls_f_time_series_class_filter accepts a data array, x[], and returns a new data array, z[], containing n_lags columns, each containing a lagged version of x.
The output data array, z, can be represented symbolically as:
z = |x(0) : x(1) : x(2) : … : x(n_lags-1)|,
where x(i) is the ith lagged column of the incoming data array, x. Notice that n_lags is the number of lags and not the maximum lag. The maximum number of lags is max_lag= n_lags-1, unless the optional input log[] is given, the highest lag is max_lags. If n_lags =2 and the optional input log[] is not given, then the output array contains the lags 0, 1.
Consider, an example in which n_obs=10, n_lags =2 and
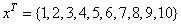 .
.
If 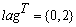 and
and
 .
.
then, n_classes=1 and z would contain 2 columns and 10 rows:
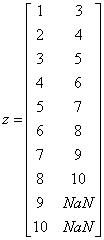 .
.
Note that since lagT = [0,1], the first column of z is formed using a lag of zero and the second is formed using a lag of two. A zero lag corresponds to no lag, which is why the first column of z in this example is equal to the original data in x.
On the other hand, if the data were organized into two classes with
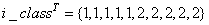 ,
,
then z is still a 2 by 10 matrix, but with the following values:
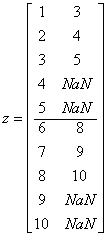
The first 5 rows of z are the lagged columns for the first class, and the last five are the lagged columns for the second class.
Example 1
Suppose that the training data to the neural network consists of the following data matrix consisting of a single nominal variable coded into two binary columns and a single time series variable:
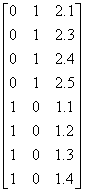
In this case, n_obs=8 and n_classes=2. If we wanted to lag the 3rd column by 2 time lags, i.e., n_lags=2,
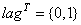 ,
,
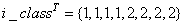 , and
, and
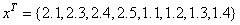 .
.
The resulting data matrix would have 4 rows and 2 columns:
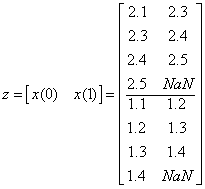 .
.
void main(){
#define N_OBS 8
#define N_LAGS 2
float x[N_OBS] = {2.1, 2.3, 2.4, 2.5, 1.1, 1.2, 1.3, 1.4};
float *z;
int n_classes = 2;
int i_class[] = {1,1,1,1,2,2,2,2};
z = imsls_f_time_series_class_filter(N_OBS, N_LAGS, n_classes,
i_class, x,
0);
imsls_f_write_matrix("z", N_OBS, N_LAGS, (float*)z, 0);
}
Output
z
1 2
1 2.1 2.3
2 2.3 2.4
3 2.4 2.5
4 2.5 ...........
5 1.1 1.2
6 1.2 1.3
7 1.3 1.4
8 1.4 ...........
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |