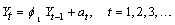Estimates missing values in a time series.
Synopsis
float *imsls_f_estimate_missing(int n_obs, int tpoints[],
float z[],…,0)
The type double function is imsls_d_estimate_missing.
Required Arguments
int n_obs
(Input)
Number of non-missing observations in the
time series. The time series must not contain gaps with more than 3 missing
values.
int tpoints[] (Input)
Vector of length
n_obs containing the
time points 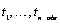 at
which the time series values were observed. The time points must be in strictly
increasing order. Time points for missing values must lie in the open interval
at
which the time series values were observed. The time points must be in strictly
increasing order. Time points for missing values must lie in the open interval
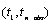 .
.
float z[] (Input)
Vector
of length n obs
containing the time series values. The values must be ordered in accordance with
the values in vector tpoints. It is assumed
that the time series after estimation of missing values contains values at
equidistant time points where the distance between two consecutive time points
is one. If the non-missing time series values are observed at time points
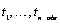 , then missing values
between
, then missing values
between 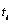 and
and
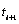 ,
, 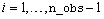 , exist if
, exist if 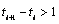 . The size of the gap between
. The size of the gap between
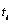 and
and
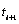 is then
is then
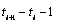 . The total length of
the time series with non-missing and estimated missing values is
. The total length of
the time series with non-missing and estimated missing values is 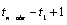 ,
or tpoints[n_obs-1]-tpoints[0]+1.
,
or tpoints[n_obs-1]-tpoints[0]+1.
Return Value
Pointer to an array of length (tpoints[n_obs-1]-tpoints[0]+1) containing the time series together with estimates for the missing values. If an error occurred, NULL is returned.
Synopsis with Optional Arguments
float *imsls_f_estimate_missing (int n_obs, int tpoints[], float z[],
IMSLS_METHOD, int method,
IMSLS_MAX_LAG, int maxlag,
IMSLS_NTIMES, int *ntimes,
IMSLS_MEAN_ESTIMATE, float mean_estimate,
IMSLS_CONVERGENCE_TOLERANCE,
float convergence_tolerance,
IMSLS_RELATIVE_ERROR, float
relative_error,
IMSLS_MAX_ITERATIONS, int
max_iterations,
IMSLS_TIMES_ARRAY, int **times,
IMSLS_TIMES_ARRAY_USER,
int times[],
IMSLS_MISSING_INDEX, int
**missing_index,
IMSLS_MISSING_INDEX_USER, int
missing_index[],
IMSLS_RETURN_USER, float u_z[],
0)
Optional Arguments
IMSLS_METHOD, int
method
(Input)
The method used for estimating the missing values:
0 — Use median.
1 — Use cubic spline
interpolation.
2 — Use one-step-ahead forecasts from an AR(1)
model.
3 — Use one-step-ahead forecasts from an AR(p) model.
Default: method = 3
If
method = 2 is chosen,
then all values of gaps beginning at time points 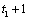 or
or 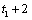 are estimated by method 0. If method = 3 is
chosen and the first gap starts at
are estimated by method 0. If method = 3 is
chosen and the first gap starts at 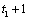 , then the values of this gap are also estimated by method 0. If the
length of the series before a gap, denoted len, is greater than 1
and less than 2
, then the values of this gap are also estimated by method 0. If the
length of the series before a gap, denoted len, is greater than 1
and less than 2 maxlag, then maxlag is
reduced to len/2 for the
computation of the missing values within this gap.
maxlag, then maxlag is
reduced to len/2 for the
computation of the missing values within this gap.
IMSLS_MAX_LAG,
int maxlag (Input)
Maximum lag number
when method = 3 was chosen.
Default: maxlag = 10
IMSLS_NTIMES, int
*ntimes
(Output)
Number of elements in the time series with estimated missing
values. Note that ntimes =
tpoints[n_obs-1]-tpoints[0]+1.
IMSLS_MEAN_ESTIMATE,
float mean_estimate
(Input)
Estimate of the
mean of the time series.
IMSLS_CONVERGENCE_TOLERANCE,
float convergence_tolerance
(Input)
Tolerance level used to determine convergence of the nonlinear least
squares algorithm used in method 2. Argument convergence_tolerance
represents the minimum relative decrease in the sum of squares between
two iterations required to determine convergence. Hence, convergence_tolerance
must be greater than or equal to 0.
Default: 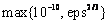 for single precision and
for single precision and
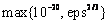 for double
precision, where eps =imsls_f_machine(4)
for single precision and
for double
precision, where eps =imsls_f_machine(4)
for single precision and
eps =imsls_d_machine(4)
for double precision.
IMSLS_RELATIVE_ERROR, float
relative_error
(Input)
Stopping criterion for use in the nonlinear equation solver
used by method 2.
Default: relative_error = 100
´ imsls_f_machine(4) for
single precision, relative_error = 100
´ imsls_d_machine(4) for
double precision..
IMSLS_MAX_ITERATIONS, int
max_iterations
(Input)
Maximum number of iterations allowed in the nonlinear
equations solver used by method 2.
Default: max_iterations = 200.
IMSLS_TIMES_ARRAY,
int **times
(Output)
Address of a pointer to an internally allocated array of
length
ntimes = tpoints[n_obs-1]-tpoints[0]+1 containing the
time points of the time series with estimates for the missing values.
IMSLS_TIMES_ARRAY_USER,
int times[]
(Output)
Storage for array times is provided by the user. See IMSLS_TIMES_ARRAY.
IMSLS_MISSING_INDEX,
int **missing_index
(Output)
Address of a pointer to an internally allocated array of
length (ntimes-n_obs)
containing the indices for the missing values in array times. If ntimes-n_obs = 0, then
no missing value could be found and NULL is returned.
IMSLS_MISSING_INDEX_USER, int
missing_index[]
(Output)
Storage for array missing_index is provided by
the user. See IMSLS_MISSING_INDEX.
IMSLS_RETURN_USER,
float u_z[] (Output)
If
specified, u_z is a vector of
length tpoints[n_obs-1]-tpoints[0]+1
containing the time series values together with estimates for missing values.
Description
Traditional time series analysis as described by Box,
Jenkins and Reinsel (1994) requires the observations made at equidistant time
points 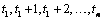 . When
observations are missing, the problem occurs to determine suitable estimates.
Function imsls_f_estimate_missing
offers 4 estimation methods:
. When
observations are missing, the problem occurs to determine suitable estimates.
Function imsls_f_estimate_missing
offers 4 estimation methods:
Method 0 estimates the missing
observations in a gap by the median of the last four time series
values before and the first four values after the gap. If not enough values are
available before or after the gap then the number is reduced
accordingly. This method is very fast and simple, but its use is limited
to stationary ergodic series without outliers and level shifts.
Method 1 uses a cubic spline interpolation method to
estimate missing values. Here the interpolation is again done over the last four
time series values before and the first four values after the gap. The missing
values are estimated by the resulting interpolant. This method gives smooth
transitions across missing values.
Method 2 assumes that the time
series before the gap can be well described by an AR(1) process. If the last
observation prior to the gap is made at time point 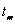 then it uses the time
series values at
then it uses the time
series values at 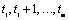 to compute the one-step-ahead forecast at origin
to compute the one-step-ahead forecast at origin
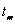 . This value is taken
as an estimate for the missing value at time point
. This value is taken
as an estimate for the missing value at time point 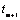 . If the value at
. If the value at 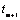 is also missing then the
values at time points
is also missing then the
values at time points 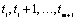 are used to recompute the AR(1) model, estimate the value
at
are used to recompute the AR(1) model, estimate the value
at 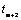 and so
on. The coefficient
and so
on. The coefficient 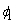 in the AR(1) model is computed internally by the method of
least squares from routine imsls_f_arma.
in the AR(1) model is computed internally by the method of
least squares from routine imsls_f_arma.
Finally, method 3 uses an AR(p) model to estimate missing
values by a one-step-ahead forecast . First, function imsls_f_auto_uni_ar,
applied to the time series prior to the missing values, is used to determine the
optimum p
from the set {0, 1, ¼, max_lag}
of possible values and to compute the parameters 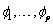 of the resulting
AR(p) model. The parameters are estimated by the least squares method based on
Householder transformations as described in Kitagawa and Akaike (1978).
Denoting the mean of the series
of the resulting
AR(p) model. The parameters are estimated by the least squares method based on
Householder transformations as described in Kitagawa and Akaike (1978).
Denoting the mean of the series 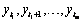 by m the
one-step-ahead forecast at origin
by m the
one-step-ahead forecast at origin 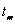 ,
, 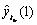 , can be computed by the formula
, can be computed by the formula
This value is used as an estimate for the missing value. The procedure starting with imsls_f_auto_uni_ar is then repeated for every further missing value in the gap. All four estimation methods treat gaps of missing values in increasing time order.
Example
We assume that 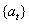 is a Gaussian white noise process,
is a Gaussian white noise process, 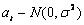 . Then,
. Then, 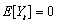 and
and 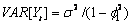 (see Anderson, p. 174).
(see Anderson, p. 174).
The time series in the code below was artificially
generated from an AR(1) process characterized by 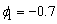 and
and 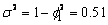 . This process is stationary
with
. This process is stationary
with 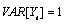 . As
initial value,
. As
initial value, 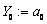 was taken. The sequence
was taken. The sequence 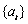 was generated by a random number
generator.
was generated by a random number
generator.
From the original series, we remove the observations at time points t=130, t=140, t=141, t=160, t=175, t=176. Then, imsls_f_estimate_missing is used to compute estimates for the missing values by all 4 estimation methods available. The estimated values are compared with the actual values.
int times_1[200], times_2[200];
int *times = NULL, *missing_index = NULL;
1.30540,-1.37166,1.47905,-0.91059,1.36191,-2.16966,3.11254,
-1.99536,2.29740,-1.82474,-0.25445,0.33519,-0.25480,-0.50574,
-0.21429,-0.45932,-0.63813,0.25646,-0.46243,-0.44104,0.42733,
0.61102,-0.82417,1.48537,-1.57733,-0.09846,0.46311,0.49156,
-1.66090,2.02808,-1.45768,1.36115,-0.65973,1.13332,-0.86285,
1.23848,-0.57301,-0.28210,0.20195,0.06981,0.28454,0.19745,
-0.16490,-1.05019,0.78652,-0.40447,0.71514,-0.90003,1.83604,
-2.51205,1.00526,-1.01683,1.70691,-1.86564,1.84912,-1.33120,
2.35105,-0.45579,-0.57773,-0.55226,0.88371,0.23138,0.59984,
0.31971,0.59849,0.41873,-0.46955,0.53003,-1.17203,1.52937,
-0.48017,-0.93830,1.00651,-1.41493,-0.42188,-0.67010,0.58079,
-0.96193,0.22763,-0.92214,1.35697,-1.47008,2.47841,-1.50522,
0.41650,-0.21669,-0.90297,0.00274,-1.04863,0.66192,-0.39143,
0.40779,-0.68174,-0.04700,-0.84469,0.30735,-0.68412,0.25888,
-1.08642,0.52928,0.72168,-0.18199,-0.09499,0.67610,0.14636,
0.46846,-0.13989,0.50856,-0.22268,0.92756,0.73069,0.78998,
-1.01650,1.25637,-2.36179,1.99616,-1.54326,1.38220,0.19674,
-0.85241,0.40463,0.39523,-0.60721,0.25041,-1.24967,0.26727,
1.40042,-0.66963,1.26049,-0.92074,0.05909,-0.61926,1.41550,
0.25537,-0.13240,-0.07543,0.10413,1.42445,-1.37379,0.44382,
-1.57210,2.04702,-2.22450,1.27698,0.01073,-0.88459,0.88194,
-0.25019,0.70224,-0.41855,0.93850,0.36007,-0.46043,0.18645,
0.06337,0.29414,-0.20054,0.83078,-1.62530,2.64925,-1.25355,
1.59094,-1.00684,1.03196,-1.58045,2.04295,-2.38264,1.65095,
-0.33273,-1.29092,0.14020,-0.11434,0.04392,0.05293,-0.42277,
0.59143,-0.03347,-0.58457,0.87030,0.19985,-0.73500,0.73640,
0.29531,0.22325,-0.60035,1.42253,-1.11278,1.30468,-0.41923,
-0.38019,0.50937,0.23051,0.46496,0.02459,-0.68478,0.25821,
1.17655,-2.26629,1.41173,-0.68331
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,
25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,
46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,
67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,
88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,
107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,
123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,
139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,
155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,
171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,
187,188,189,190,191,192,193,194,195,196,197,198,199,200
times_1[0] = times_2[0] = tpoints[0];
/* Generate series with missing values */
if ( i!=129 && i!= 139 && i!=140 && i!=159 && i!=174 && i!=175 )
result = imsls_f_estimate_missing(n_obs, times_2, x_2,
IMSLS_MISSING_INDEX, &missing_index,
result = imsls_f_estimate_missing(n_obs, times_2, x_2,
IMSLS_MISSING_INDEX, &missing_index,
if (j == 0) printf("\nMethod: Median\n");
if (j == 1) printf("\nMethod: Cubic Spline Interpolation\n");
if (j == 2) printf("\nMethod: AR(1) Forecast\n");
if (j == 3) printf("\nMethod: AR(p) Forecast\n");
printf("ntimes = %d\n", ntimes);
printf("time\tactual\tpredicted\tdifference\n");
printf("%d, %10.5f, %10.5f, %18.6f\n", times[miss_ind],
x_1[miss_ind], result[miss_ind],
fabs(x_1[miss_ind]-result[miss_ind]));
Output
time actual predicted difference
130, -0.92074, 0.26132, 1.182060
140, 0.44382, 0.05743, 0.386390
141, -1.57210, 0.05743, 1.629530
160, 2.64925, 0.04680, 2.602450
175, -0.42277, 0.04843, 0.471195
176, 0.59143, 0.04843, 0.543005
Method: Cubic Spline Interpolation
time actual predicted difference
130, -0.92074, 1.54109, 2.461829
140, 0.44382, -0.40730, 0.851119
141, -1.57210, 2.49709, 4.069194
160, 2.64925, -2.94712, 5.596371
175, -0.42277, 0.25066, 0.673430
176, 0.59143, 0.38032, 0.211107
time actual predicted difference
130, -0.92074, -0.92971, 0.008968
140, 0.44382, 1.02824, 0.584424
141, -1.57210, -0.74527, 0.826832
160, 2.64925, 1.22880, 1.420454
175, -0.42277, 0.01049, 0.433259
176, 0.59143, 0.03683, 0.554601
time actual predicted difference
130, -0.92074, -0.86385, 0.056894
140, 0.44382, 0.98098, 0.537164
141, -1.57210, -0.64489, 0.927206
160, 2.64925, 1.18966, 1.459592
175, -0.42277, -0.00105, 0.421722
176, 0.59143, 0.03773, 0.553705
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |