Computes estimates of the parameters of a GARCH(p,q) model.
Synopsis
#include <imsls.h>
float *imsls_f_garch (int p, int q, int m, float y[], float xguess[], …, 0)
The type double function is imsls_d_garch.
Required Arguments
int p
(Input)
Number of GARCH parameters.
int q
(Input)
Number of ARCH parameters.
int m
(Input)
Length of the observed time series.
float y[]
(Input)
Array of length m containing the
observed time series data.
float xguess[]
(Input)
Array of length p + q + 1 containing the initial values for the parameter array x[].
Return Value
Pointer to the parameter array x[] of length p + q + 1 containing the estimated values of sigma squared, followed by the q ARCH parameters, and the p GARCH parameters.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_garch (int
p, int q, int m, float
y[],
float
xguess[],
IMSLS_MAX_SIGMA,
float max_sigma,
IMSLS_A,
float *a,
IMSLS_AIC,
float *aic,
IMSLS_VAR,
float *var,
IMSLS_VAR_USER,
float var[],
IMSLS_VAR_COL_DIM,
int var_col_dim,
IMSLS_RETURN_USER,
float x[],
0)
Optional Arguments
IMSLS_MAX_SIGMA, float
max_sigma, (Input)
Value of the
upperbound on the first element (sigma) of the array of returned estimated
coefficients. Default = 10.
IMSLS_A,
float *a, (Output)
Value of
Log-likelihood function evaluated at the estimated parameter array x.
IMSLS_AIC, float
*aic, (Output)
Value of Akaike
Information Criterion evaluated at the estimated parameter array x.
IMSLS_VAR, float
*var, (Output)
Array of size
(p+q+1)x(p+q+1) containing the variance-covariance
matrix.
IMSLS_VAR_USER, float
var[], (Output)
Storage for array
var is provided by the user.
See IMSLS_VAR.
IMSLS_VAR_COL_DIM, int
var_col_dim, (Input)
Column
dimension (p+q+1)of the variance-covariance matrix.
IMSLS_RETURN_USER, float
x[], (Output)
If specified,
x returns an array of length p +q + 1 containing the
estimated values of sigma squared, followed by the q ARCH parameters, and
the p GARCH parameters. Storage for estimated parameter array x is
provided by the user.
Description
The Generalized Autoregressive Conditional Heteroskedastic
(GARCH) model for a time series  is defined as
is defined as

where zt's are independent and identically distributed standard normal random variables,
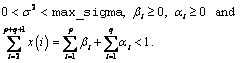
The above model is denoted as
GARCH(p,q). The bi and ai
coeffecients will be referred to as GARCH and ARCH coefficents,
respectively. When bi = 0,
i =
1,2,…,p, the above model reduces to ARCH(q) which was proposed by
Engle (1982). The nonnegativity conditions on the parameters imply a nonnegative
variance and the condition on the sum of the bi's and a i's is required for wide
sense stationarity.
In the empirical analysis of observed data, GARCH(1,1) or GARCH(1,2) models have often found to appropriately account for conditional heteroskedasticity (Palm 1996). This finding is similar to linear time series analysis based on ARMA models.
It is important to notice that for the above models positive and negative past values have a symmetric impact on the conditional variance. In practice, many series may have strong asymmetric influence on the conditional variance. To take into account this phenomena, Nelson (1991) put forward Exponential GARCH (EGARCH). Lai (1998) proposed and studied some properties of a general class of models that extended linear relationship of the conditional variance in ARCH and GARCH into nonlinear fashion.
The maximum likelihood method is used in estimating the parameters in GARCH(p,q). The log-likelihood of the model for the observed series {wt} with length m = nobs is

Thus log(L) is maximized subject to the constraints on the αi, bi, and s.
In this model, if q = 0, the GARCH model is singular since the estimated Hessian matrix is singular.
The initial values of the parameter vector x entered in vector xguess must satisfy certain constraints. The first element of xguess refers to s2 and must be greater than zero and less than max_sigma. The remaining p+q initial values must each be greater than or equal to zero and sum to a value less than one.
To guarantee stationarity in model fitting,
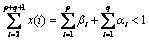
is checked internally. The initial values should selected from values between zero and one.
AIC is computed by
- 2 log (L) + 2(p+q+1),
where log(L) is the value of the log-likelihood function.
Statistical inferences can be performed outside the routine GARCH based on the output of the log-likelihood function (A), the Akaike Information Criterion (AIC), and the variance-covariance matrix (VAR).
Example
The data for this example are generated to follow a GARCH(p,q) process by using a random number generation function sgarch. The data set is analyzed and estimates of sigma, the ARCH parameters, and the GARCH parameters are returned. The values of the Log-likelihood function and the Akaike Information Criterion are returned from the optional arguments IMSLS_A and IMSLS_AIC.
#include <imsls.h>
#include <math.h>
static void sgarch (int p, int q, int m, float x[],
float y[], float z[], float y0[], float sigma[]);
#define M 1000
#define N (P + Q + 1)
#define P 2
#define Q 1
int main ()
{
int n, p, q, m;
float a, aic, wk1[M + 1000], wk2[M + 1000],
wk3[M + 1000], x[N], xguess[N], y[M];
float *result;
imsls_random_seed_set (182198625);
m = M;
p = P;
q = Q;
n = p+q+1;
x[0] = 1.3;
x[1] = .2;
x[2] = .3;
x[3] = .4;
xguess[0] = 1.0;
xguess[1] = .1;
xguess[2] = .2;
xguess[3] = .3;
sgarch (p, q, m, x, y, wk1, wk2, wk3);
result = imsls_f_garch(p, q, m, y, xguess,
IMSLS_A, &a,
IMSLS_AIC, &aic,
0);
printf("Sigma estimate is\t%11.4f\n", result[0]);
printf("ARCH(1) estimate is\t%11.4f\n", result[1]);
printf("GARCH(1) estimate is\t%11.4f\n", result[2]);
printf("GARCH(2) estimate is\t%11.4f\n", result[3]);
printf("\nLog-likelihood function value is\t%11.4f\n", a);
printf("Akaike Information Criterion value is\t%11.4f\n", aic);
return;
}
static void sgarch (int p, int q, int m, float x[],
float y[], float z[], float y0[], float sigma[])
{
int i, j, l;
float s1, s2, s3;
imsls_f_random_normal ( m + 1000, IMSLS_RETURN_USER, z, 0);
l = imsls_i_max (p, q);
l = imsls_i_max (l, 1);
for (i = 0; i < l; i++) y0[i] = z[i] * x[0];
/* COMPUTE THE INITIAL VALUE OF SIGMA */
s3 = 0.0;
if (imsls_i_max (p, q) >= 1) {
for (i = 1; i < (p + q + 1); i++) s3 += x[i];
}
for (i = 0; i < l; i++) sigma[i] = x[0] / (1.0 - s3);
for (i = l; i < (m + 1000); i++) {
s1 = 0.0;
s2 = 0.0;
if (q >= 1) {
for (j = 0; j < q; j++)
s1 += x[j + 1] * y0[i - j - 1] * y0[i - j - 1];
}
if (p >= 1) {
for (j = 0; j < p; j++)
s2 += x[q + 1 + j] * sigma[i - j - 1];
}
sigma[i] = x[0] + s1 + s2;
y0[i] = z[i] * sqrt (sigma[i]);
}
/*
* DISCARD THE FIRST 1000 SIMULATED OBSERVATIONS
*/
for (i = 0; i < m; i++) y[i] = y0[1000 + i];
return;
} /* end of function */
Output
Sigma estimate is 1.6480
ARCH(1) estimate is 0.2427
GARCH(1) estimate is 0.3175
GARCH(2) estimate is 0.3335
Log-likelihood function value is -2707.0903
Akaike Information Criterion value is 5422.1807
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |