Performs a Kolmogorov-Smirnov two-sample test.
Synopsis
#include <imsls.h>
float *imsls_f_kolmogorov_two (int n_observations_x, float x[], int n_observations_y, float y[], ..., 0)
The type double function is imsls_d_kolmogorov_two.
Required Arguments
int
n_observations_x (Input)
Number of observations in sample
one.
float x[]
(Input)
Array of size n_observations_x
containing the observations from sample one.
int
n_observations_y (Input)
Number of observations in sample
two.
float y[]
(Input)
Array of size n_observations_y
containing the observations from sample two.
Return Value
Pointer to an array of length 3 containing Z, p1, and p2 .
Synopsis with Optional Arguments
#include <imsls.h>
float *imsls_f_kolmogorov_two
(int
n_observations_x, float
x[],
int n_observations_y, float y[],
IMSLS_DIFFERENCES, float **differences,
IMSLS_DIFFERENCES_USER, float
differences[],
IMSLS_N_MISSING_X, int *xmissing,
IMSLS_N_MISSING_Y, int *ymissing,
IMSLS_RETURN_USER, float
test_statistic[],
0)
Optional Arguments
IMSLS_DIFFERENCES, float
**differences (Output)
Address of a pointer to the
internally allocated array containing
Dn ,
Dn+, Dn-.
IMSLS_DIFFERENCES_USER, float differences[]
(Output)
Storage for array differences is
provided by the user.
See IMSLS_DIFFERENCES.
IMSLS_N_MISSING_X, int *xmissing
(Ouput)
Number of missing values in the x sample is returned
in *xmissing.
IMSLS_N_MISSING_Y, int *ymissing
(Ouput)
Number of missing values in the y sample is returned
in *ymissing.
IMSLS_RETURN_USER, float
test_statistics[] (Output)
If specified, the
Z-score and the p-values for hypothesis test against both
one-sided and two-sided alternatives is stored in array test_statistics
provided by the user.
Description
Function imsls_f_kolmogorov_two computes Kolmogorov-Smirnov two-sample test statistics for testing that two continuous cumulative distribution functions (CDF's) are identical based upon two random samples. One- or two-sided alternatives are allowed. Exact p-values are computed for the two-sided test when n_observations_x * n_observations_y is less than 104.
Let Fn(x) denote the
empirical CDF in the X sample, let Gm(y) denote the
empiri-
cal CDF in the Y sample, where n = n_observations_x
- n_missing_x
and m = n_observations_y
- n_missing_y,
and let the corresponding population distribution functions be denoted by
F(x) and G(y), respectively. Then, the hypotheses
tested by imsls_f_kolmogorov_two
are as follows:
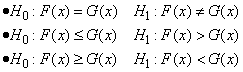
The test statistics are given as follows:

Asymptotically, the distribution of the statistic
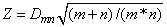
(returned in test_statistics[0]) converges to a distribution given by Smirnov (1939).
Exact probabilities for the two-sided test are computed
when n*m is less than or equal to 104, according to an
algorithm given by Kim and Jennrich (1973;).
When n*m is greater than 104, the very good
approximations given by Kim and Jennrich are used to obtain the two-sided
p-values. The one-sided probability is taken as one half the two-sided
probability. This is a very good approximation when the p-value is small
(say, less than 0.10) and not very good for large
p-values.
Example
This example illustrates the imsls_f_kolmogorov_two routine with two randomly generated samples from a uniform(0,1) distribution. Since the two theoretical distributions are identical, we would not expect to reject the null hypothesis.
#include <imsls.h>
#include <stdio.h>
int main()
{
float *statistics=NULL, *diffs = NULL, *x=NULL, *y=NULL;
int nobsx = 100, nobsy = 60, nmissx, nmissy;
imsls_random_seed_set(123457);
x = imsls_f_random_uniform(nobsx, 0);
y = imsls_f_random_uniform(nobsy, 0);
statistics = imsls_f_kolmogorov_two(nobsx, x, nobsy, y,
IMSLS_N_MISSING_X, &nmissx,
IMSLS_N_MISSING_Y, &nmissy,
IMSLS_DIFFERENCES, &diffs,
0);
printf("D = %8.4f\n", diffs[0]);
printf("D+ = %8.4f\n", diffs[1]);
printf("D- = %8.4f\n", diffs[2]);
printf("Z = %8.4f\n", statistics[0]);
printf("Prob greater D one sided = %8.4f\n", statistics[1]);
printf("Prob greater D two sided = %8.4f\n", statistics[2]);
printf("Missing X = %d\n", nmissx);
printf("Missing Y = %d\n", nmissy);
}
Output
D = 0.1800
D+ = 0.1800
D- = 0.0100
Z = 1.1023
Prob greater D one sided = 0.0720
Prob greater D two sided = 0.1440
Missing X = 0
Missing Y = 0
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |