Computes Mardia's multivariate measures of skewness and kurtosis and tests for multivariate normality.
Synopsis
#include <imsls.h>
float
*imsls_f_multivar_normality_test (int
n_observations,
int n_variables, float x[], ..., 0)
The type double function is imsls_d_multivar_normality_test.
Required Arguments
int
n_observations (Input)
Number of observations (number of
rows of data) x.
int
n_variables (Input)
Dimenionality of the multivariate
space for which the skewness and kurtosis are to be computed. Number of
variables in x.
float x[]
(Input)
Array of size n_observations by
n_variables
containing the data.
Return Value
A pointer to an array of dimension 13 containing output statistics
I stat[ I ]
0 estimated skewness
1 expected skewness assuming a multivariate normal distribution
2 asymptotic chi-squared statistic assuming a multivariate normal distribution
3 probability of a greater chi-squared
4 Mardia and Foster's standard normal score for skewness
5 estimated kurtosis
6 expected kurtosis assuming a multivariate normal distribution
7 asymptotic standard error of the estimated kurtosis
8 standard normal score obtained from stat[5] through stat[7]
9 p-value corresponding to stat[8]
10 Mardia and Foster's standard normal score for kurtosis
11 Mardia's SW statistic based upon stat[4] and stat[10]
12 p-value for stat[11]
Synopsis with Optional Arguments
#include <imsls.h>
float
imsls_f_multivar_normality_test (int
n_observations_x,
int
n_variables, float x[],
IMSLS_FREQUENCIES, float
frequencies[],
IMSLS_WEIGHTS, float
weights[],
IMSLS_SUM_FREQ, int
*sum_frequencies,
IMSLS_SUM_WEIGHTS, float
*sum_weights,
IMSLS_N_ROWS_MISSING, int
*nrmiss,
IMSLS_MEANS, float
**means,
IMSLS_MEANS_USER, float
means[],
IMSLS_R, float
**R_matrix,
IMSLS_R_USER, float
R_matrix[],
IMSLS_RETURN_USER, float
test_statistics[],
0)
Optional Arguments
IMSLS_FREQUENCIES, float
frequencies[]
(Input)
Array of size n_rows containing the frequencies. Frequencies
must be integer valued. Default assumes all frequencies equal one.
IMSLS_WEIGHTS, float
weights[]
(Input)
Array of size n_rows containing the weights. Weights must be
greater than non-negative. Default assumes all weights equal one.
IMSLS_SUM_FREQ, int
*sum_frequencies
(Output)
The sum of the frequencies of all observations used in the
computations.
IMSLS_SUM_WEIGHTS,
float *weights[]
(Output)
The sum of the weights times the frequencies for all observations
used in the computations.
IMSLS_N_ROWS_MISSING,
int *nrmiss
(Output)
Number of rows of data in x[] containing any
missing values (NaN).
IMSLS_MEANS, float **means
(Output)
The address of a
pointer to an array of length n_variables
containing the sample means.
IMSLS_MEANS_USER, float means[] (Output)
Storage for
array means is
provided by user. See IMSLS_MEANS.
IMSLS_R,
float **R_matrix
(Output)
The address of a pointer to an n_variables by n_variables upper
triangular matrix containing the Cholesky RTR factorization of
the covariance matrix.
IMSLS_R_USER,
float
R_matrix[] (Output)
Storage for array R_matrix is provided
by user. See
IMSLS_R.
IMSLS_RETURN_USER, float stat[]
(Output)
User supplied array of dimension 13 containing the estimates and
their associated test statistics.
Description
Function imsls_f_multivar_normality_test
computes Mardia's (1970) measures b1,p and b2,p of multivariate
skewness and kurtosis, respectfully, for p = n_variables.
These measures are then used in computing tests for multivariate normality.
Three test statistics, one based upon b1,p alone, one based upon
b2,p alone, and an omnibus
test statistic formed by combining normal scores obtained from b1,p and b2,p are computed. On the
order of np3, operations are
required in computing
b1,p when the method of
Isogai (1983) is used, where n = n_observations.
On the order of np2, operations are
required in computing b2,p.
Let
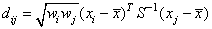
where

fi is the frequency of the i-th observation, and wi is the weight for this observation. (Weights wi are defined such that xi is distributed according to a multivariate normal, N(m, S/wi) distribution, where S is the covariance matrix.) Mardia's multivariate skewness statistic is defined as:
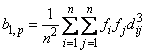
while Mardia's kurtosis is given as:
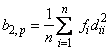
Both measures are invariant under the affine (matrix)
transformation AX + D,
and reduce to the univariate measures
when p = n_variables = 1. Using formulas given in
Mardia and Foster (1983), the approximate expected value, asymptotic standard
error, and asymptotic p-value for b2,p, and the approximate
expected value, an asymptotic chi-squared statistic, and p-value for the
b1,p statistic are
computed. These statistics are all computed under the null hypothesis of a
multivariate normal distribution. In addition, standard normal scores
W1(b1,p) and W2(b2,p) (different from but
similar to the asymptotic normal and chi-squared statistics above) are computed.
These scores are combined into an asymptotic chi-squared statistic with two
degrees of freedom:

This chi-squared statistic may be used to test for
multivariate normality.
A p-value for the chi-squared statistic is
also computed.
Example
In this example, 150 observations from a 5 dimensional standard normal distribution are generated via routine imsls_f_random_normal (Chapter 12, “Random Number Generation”;). The skewness and kurtosis statistics are then computed for these observations.
#include <imsls.h>
#include <stdio.h>
int main()
{
float *x, swt, *xmean, *r, *stats;
int nobs = 150, ncol = 5, nvar = 5, izero = 0, ni, nrmiss;
imsls_random_seed_set(123457);
x = imsls_f_random_normal(nobs*nvar, 0);
stats = imsls_f_multivar_normality_test(nobs, nvar, x,
IMSLS_SUM_FREQ, &ni,
IMSLS_SUM_WEIGHTS, &swt,
IMSLS_N_ROWS_MISSING, &nrmiss,
IMSLS_R, &r,IMSLS_MEANS, &xmean,
0);
printf("Sum of frequencies = %d\nSum of the weights =%8.3f\n",
ni, swt);
printf(" Number rows missing = %3d\n", nrmiss);
imsls_f_write_matrix("stat", 13, 1, stats,
IMSLS_ROW_NUMBER_ZERO, 0);
imsls_f_write_matrix("means", 1, nvar, xmean, 0);
imsls_f_write_matrix("R", nvar, nvar, r, 0);
}
Output
Sum of frequencies = 150
Sum of the weights = 150.000
Number rows missing = 0
stat
0 0.73
1 1.36
2 18.62
3 0.99
4 -2.37
5 32.67
6 34.54
7 1.27
8 -1.48
9 0.14
10 1.62
11 8.24
12 0.02
means
1 2 3 4 5
0.02623 0.09238 0.06536 0.09819 0.05639
R
1 2 3 4 5
1 1.033 -0.084 -0.065 0.108 0.067
2 0.000 1.049 -0.097 -0.042 -0.021
3 0.000 0.000 1.063 0.006 -0.145
4 0.000 0.000 0.000 0.942 -0.084
5 0.000 0.000 0.000 0.000 0.949
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |