Fits a multiple linear regression model using criteria other than least squares. Namely, imsls_f_Lnorm_regression allows the user to choose Least Absolute Value (L1), Least Lp norm (Lp ), or Least Maximum Value (Minimax or L∞ ) method of multiple linear regression.
Synopsis
#include <imsls.h>
float *imsls_f_Lnorm_regression (int n_rows, int n_independent, float x[], float y[], ..., 0)
The type double function is imsls_d_Lnorm_regression.
Required Arguments
int n_rows
(Input)
Number of rows in x.
int
n_independent (Input)
Number of independent (explanatory)
variables.
float x[]
(Input)
Array of size n_rows ´ n_independent
containing the independent (explanatory) variables(s). The i-th column of
x contains the i-th independent variable.
float y[]
(Input)
Array of size n_rows containing the
dependent (response) variable.
Return Value
imsls_f_Lnorm_regression returns a pointer to an array of length n_independent + 1 containing a least absolute value solution for the regression coefficients. The estimated intercept is the initial component of the array, where the i-th component contains the regression coefficients for the i-th dependent variable. If the optional argument IMSLS_NO_INTERCEPT is used then the (i-1)-st component contains the regression coefficients for the i-th dependent variable. imsls_f_Lnorm_regression returns the Lp norm or least maximum value solution for the regression coefficients when appropriately specified in the optional argument list.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_Lnorm_regression (int n_rows, int n_independent, float x[], float y[],
IMSLS_METHOD_LAV,
IMSLS_METHOD_LLP, float p,
IMSLS_METHOD_LMV,
IMSLS_X_COL_DIM, int
x_col_dim,
IMSLS_INTERCEPT,
IMSLS_NO_INTERCEPT,
IMSLS_RANK, int
*rank,
IMSLS_ITERATIONS, int
*iterations,
IMSLS_N_ROWS_MISSING, int
*n_rows_missing,
IMSLS_TOLERANCE, float tolerence,
IMSLS_SEA, float *sum_lav_error,
IMSLS_MAX_RESIDUAL, float *max_residual,
IMSLS_R, float **R_matrix,
IMSLS_R_USER, float R_matrix[],
IMSLS_DEGREES_OF_FREEDOM,
float
df_error,
IMSLS_SCALE, float *square_of_scale,
IMSLS_RESIDUALS_LP_NORM, float *Lp_norm_residual,
IMSLS_EPS, float epsilon,
IMSLS_WEIGHTS, float weights[],
IMSLS_FREQUENCIES, float
frequencies[],
IMSLS_RETURN_USER, float
coefficients[],
0)
Optional Arguments
IMSLS_METHOD_LAV, or
IMSLS_METHOD_LLP, float p, (Input) or
IMSLS_METHOD_LMV,
By default (or if IMSLS_METHOD_LAV is
specified) the function fits a multiple linear regression model using the least
absolute values criterion.
IMSLS_METHOD_LLP
requires the argument p, for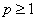 , and fits a multiple linear regression model using the
Lp norm criterion.
, and fits a multiple linear regression model using the
Lp norm criterion.
IMSLS_METHOD_LMV fits a multiple linear regression model using the minimax criterion.
IMSLS_WEIGHTS,
float weights[], (Input)
Array of size n_rows containing the
weights for the independent (explanatory) variable.
IMSLS_FREQUENCIES,
float frequencies[], (Input)
Array of size n_rows containing the
frequencies for the independent (explanatory) variable.
IMSLS_X_COL_DIM, int x_col_dim, (Input)
Leading dimension of
x exactly as
specified in the dimension statement in the calling program.
IMSLS_INTERCEPT, or
IMSLS_NO_INTERCEPT,
IMSLS_INTERCEPT is the
default where the fitted value for observation i is
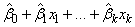
where k = n_independent. If IMSLS_NO_INTERCEPT is specified, the intercept term

is omitted from the model and the return value from regression is a pointer to an array of length n_independent.
IMSLS_RANK, int *rank, (Output)
Rank of the fitted model is returned
in *rank.
IMSLS_ITERATIONS, int *iterations, (Output)
Number of iterations performed.
IMSLS_N_ROWS_MISSING, int *n_rows_missing, (Output)
Number of rows of data
containing NaN (not a number) for the
dependent or independent variables. If a row of data contains NaN
for any of these variables, that row is excluded from the computations.
IMSLS_RETURN_USER, float
coefficients[] (Output)
Storage for array coefficients is provided by the user.
See Return Value.
If IMSLS_METHOD_LAV is specified:
IMSLS_SEA, float sum_lav_error, (Output)
Sum of the absolute value of the
errors.
If IMSLS_METHOD_LMV is specified:
IMSLS_MAX_RESIDUAL, float max_residual, (Output)
Magnitude of the largest
residual.
If IMSLS_METHOD_LLP is specified:
IMSLS_TOLERANCE, float tolerence, (Input)
Tolerance used in determining linear dependence.
tolerence = 100 *
imsls_f_machine(4) is the default.
For more details see Chapter 15,
“Ultilities” function imsls_f_machine.
IMSLS_R, float
**R_matrix, (Output)
Upper triangular matrix of dimension
(number of coeffieciencts
by number of coeffecients) containing the R matrix
from a QR decomposition of the matrix of regressors.
IMSLS_R_USER, float R_matrix[], (Output)
Storage for array R_matrix is provided
by the user. See IMSLS_R.
IMSLS_DEGREES_OF_FREEDOM, float df_error, (Output)
Sum of the frequencies minus *rank. In least
squares fit (p =2) df_error is called the
degrees of freedom of error.
IMSLS_RESIDUALS, float
**residual, (Output)
Address of a pointer to an array of
length n_rows
(equal to the number of observations) containing the residuals.
IMSLS_RESIDUALS_USER, float residual[], (Output)
Storage for array residual is provided by the user.
See IMSLS_RESIDUALS.
IMSLS_SCALE, float
*square_of_scale, (Output)
Square
of the scale constant used in an Lp analysis. An estimated
asymptotic variance-covariance matrix of the regression coefficients is square_of_scale *
(RTR)-1.
IMSLS_RESIDUALS_LP_NORM, float
*Lp_norm_residual,
(Output)
Lp norm of the residuals.
IMSLS_EPS, float epsilon, (Input)
Convergence criterion. If the maximum
relative difference in residuals from the
k-th to (k+1)-st iterations is less than epsilon, convergence
is declared. epsilon =
100 * machine(4) is the default.
Description
Least Absolute Value Criterion
Function imsls_f_Lnorm_regression computes estimates of the regression coefficients in a multiple linear regression model. For optional argument IMSLS_LAV (default), the criterion satisfied is the minimization of the sum of the absolute values of the deviations of the observed response yi from the fitted response
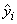
for a set on n observations. Under this criterion, known as the L1 or LAV (least absolute value) criterion, the regression coefficient estimates minimize
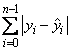
The estimation problem can be posed as a linear programming problem. The special nature of the problem, however, allows for considerable gains in efficiency by the modification of the usual simplex algorithm for linear programming. These modifications are described in detail by Barrodale and Roberts (1973, 1974).
In many cases, the algorithm can be made faster by computing a least-squares solution prior to the invocation of IMSLS_LAV. This is particularly useful when a least-squares solution has already been computed. The procedure is as follows:
1. Fit the
model using least squares and compute the residuals from
this fit.
2. Fit the residuals from Step 1 on the regressor variables in the model using IMSLS_LAV.
3 Add
the two estimated regression coefficient vectors from Steps 1
and 2. The
result is an L1 solution.
When multiple solutions exist for a given problem, option IMSLS_LAV may yield different estimates of the regression coefficients on different computers, however, the sum of the absolute values of the residuals should be the same (within rounding differences). The informational error indicating nonunique solutions may result from rounding accumulation. Conversely, because of rounding the error may fail to result even when the problem does have multiple solutions.
Lp Norm Criterion
Optional argument IMSLS_LLP computes estimates of the regression coefficients in a multiple linear regression model y = Xb + e under the criterion of minimizing the Lp norm of the deviations for i = 0, ¼, n-1 of the observed response yi from the fitted response
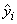
for a set on n observations and for p ³ 1. For the case when IMSLS_WEIGHTS and IMSLS_FREQUENCIES are not supplied, the estimated regression coefficient vector,
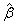
(output in coefficients[]) minimizes the Lp norm
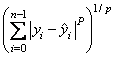
The choice p = 1 yields the maximum likelihood estimate for b when the errors have a Laplace distribution. The choice p = 2 is best for errors that are normally distributed. Sposito (1989, pages 36−40) discusses other reasonable alternatives for p based on the sample kurtosis of the errors.
Weights are useful if the errors in the model have known unequal variances
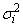
In this case, the weights should be taken as

Frequencies are useful if there are repetitions of some
observations in the data set. If a single row of data corresponds to
ni observations, set the
frequency fi = ni.
In general, IMSLS_LLP
minimizes the Lp norm
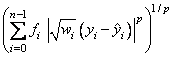
The asymptotic variance-covariance matrix of the estimated regression coefficients is given by
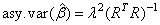
where R is from the QR
decomposition of the matrix of regressors (output in
R-Matrix)ere
an estimate of l2 is output in square_of_scale.
In the discussion that follows, we will first present the algorithm with frequencies and weights all taken to be one. Later, we will present the modifications to handle frequencies and weights different from one.
Option call IMSLS_LLP uses Newton's method with a line search for p > 1.25 and, for p £ 1.25, uses a modification due to Ekblom (1973, 1987) in which a series of perturbed problems are solved in order to guarantee convergence and increase the convergence rate. The cutoff value of 1.25 as well as some of the other implementation details given in the remaining discussion were investigated by Sallas (1990) for their effect on CPU times.
In each case, for the first iteration a least-squares solution for the regression coefficients is computed using routine imsls_f_regression. If p = 2, the computations are finished. Otherwise, the residuals from the k-th iteration,
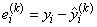
are used to compute the gradient and Hessian for the Newton step for the (k + 1)-st iteration for minimizing the p-th power of the Lp norm. (The exponent 1/p in the Lp norm can be omitted during the iterations.)
For subsequent iterations, we first discuss the p > 1.25 case. For p > 1.25, the gradient and Hessian at the (k + 1)-st iteration depend upon
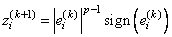
and
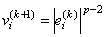
In the case 1.25 < p < 2 and
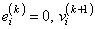
and the Hessian are undefined; and we follow the recommendation of Merle and Spath (1974). Specifically, we modify the definition of

to the following:
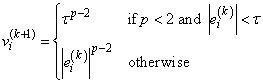
where t equals 100 * imsls_f_machine(4) (or 100.0 * imsls_d_machine(4) for the double precision version) times the square root of the residual mean square from the least-squares fit. (See routines imsls_f_machine and imsls_d_machine which are documented in the section “Machine-Dependent Constants” in Reference Material.)
Let V(k+1) be a diagonal matrix with diagonal entries

and let z(k+1) be a vector with elements
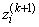
In order to compute the step on the (k + 1)-st iteration, the R from the QR decomposition of
[V(k+1)]1∕2X
is computed using fast Givens transformations. Let
R(k+1)
denote the upper triangular matrix from the QR decomposition. The linear system
[R(k+1)]TR(k+1)d(k+1)= XT z(k+1)
is solved for
d(k+1)
where R(k+1) is from the QR decomposition of
[V(k+1)]1∕2X . The step
taken on the
(k + 1)-st iteration is
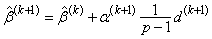
The first attempted step on the (k + 1)-st iteration is with a(k+1) = 1. If all of the
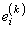
are nonzero, this is exactly the Newton step. See Kennedy and Gentle (1980, pages 528−529) for further discussion.
If the first attempted step does not lead to a decrease of at least one-tenth of the predicted decrease in the p-th power of the Lp norm of the residuals, a backtracking linesearch procedure is used. The backtracking procedure uses a one-dimensional quadratic model to estimate the backtrack constant p. The value of p is constrained to be no less that 0.1. An approximate upper bound for p is 0.5. If after 10 successive backtrack attempts, a(k) = p1p2¼ p10 does not produce a step with a sufficient decrease, then imsls_f_Lnorm_regression issues a message with error code 5. For further details on the backtrack line-search procedure, see Dennis and Schnabel (1983, pages 126−127).
Convergence is declared when the maximum relative change in the residuals from one iteration to the next is less than or equal to epsilon. The relative change

in the i-th residual from iteration k to iteration k + 1 is computed as follows:
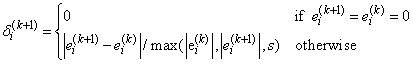
where s is the square root of the residual mean square from the least-squares fit on the first iteration.
For the case 1 £ p £ 1.25, we describe the modifications to the previous procedure that incorporate Ekblom's (1973) results. A sequence of perturbed problems are solved with a successively smaller perturbation constant c. On the first iteration, the least-squares problem is solved. This corresponds to an infinite c. For the second problem, c is taken equal to s, the square root of the residual mean square from the least-squares fit. Then, for the (j + 1)-st problem, the value of c is computed from the previous value of c according to
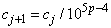
Each problem is stated as
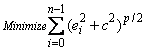
For each problem, the gradient and Hessian on the (k + 1)-st iteration depend upon

and

where

The linear system [R(k+1)]TR(k+1)d(k+1)= XTz(k+1) is solved for d(k+1) where R(k+1) is from the QR decomposition of
[V (k+1)]1∕2X. The step
taken on the
(k + 1)-st iteration is

where the first attempted step is with a(k+1) = 1. If necessary, the backtracking line-search procedure discussed earlier is used.
Convergence for each problem is relaxed somewhat by using a convergence epsilon equal to max(epsilon, 10−j) where j = 1, 2, 3, ¼ indexes the problems (j = 0 corresponds to the least-squares problem).
After the convergence of a problem for a particular c, Ekblom's (1987) extrapolation technique is used to compute the initial estimate of b for the new problem. Let R(k),
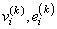
and c be from the last iteration of the last problem. Let
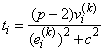
and let t be the vector with elements ti. The initial estimate of b for the new problem with perturbation constant 0.01c is
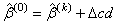
where Dc = (0.01c - c) = -0.99c, and where d is the solution of the linear system [R(k)]R(k)d = XTt.
Convergence of the sequence of problems is declared when the maximum relative difference in residuals from the solution of successive problems is less than epsilon.
The preceding discussion was limited to the case for which weights[i] = 1 and frequencies[i] = 1, i.e., the weights and frequencies are all taken equal to one. The necessary modifications to the preceding algorithm to handle weights and frequencies not all equal to one are as follows:
1. Replace

in the definitions of
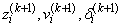
and ti.
2. Replace
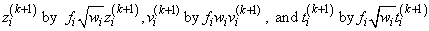
These replacements have the same effect as multiplying the i-th row of X and y by

and repeating the row fi times except for the fact that the residuals returned by imsls_f_Lnorm_regression are in terms of the original y and X.
Finally, R and an estimate of l2 are computed. Actually, R is recomputed because on output it corresponds to the R from the initial QR decomposition for least squares. The formula for the estimate of l2 depends on p.
For p = 1, the estimator for l2 is given by (McKean and Schrader 1987)
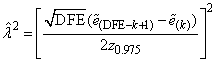
with
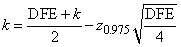
where z0.975 is the 97.5 percentile of the standard normal distribution, and where
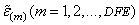
are the ordered residuals where rank zero residuals are excluded. Note that
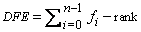
For p = 2, the estimator of l2 is the customary least-squares estimator given by
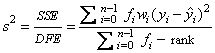
For 1 < p < 2 and for p > 2, the estimator for l2 is given by (Gonin and Money 1989)

with
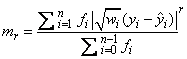
Least Minimum Value Criterion (minimax)
Optional call IMSLS_LMV
computes estimates of the regression coefficients in a multiple linear
regression model. The criterion satisfied is the minimization of the maximum
deviation of the observed response yi from the fitted
response 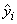 for a
set on n observations. Under this criterion, known as the minimax or LMV
(least maximum value) criterion, the regression coefficient estimates minimize
for a
set on n observations. Under this criterion, known as the minimax or LMV
(least maximum value) criterion, the regression coefficient estimates minimize
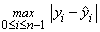
The estimation problem can be posed as a linear programming problem. A dual simplex algorithm is appropriate, however, the special nature of the problem allows for considerable gains in efficiency by modification of the dual simplex iterations so as to move more rapidly toward the optimal solution. The modifications are described in detail by Barrodale and Phillips (1975).
When multiple solutions exist for a given problem, IMSLS_LMV may yield different estimates of the regression coefficients on different computers, however, the largest residual in absolute value should have the same absolute value (within rounding differences). The informational error indicating nonunique solutions may result from rounding accumulation. Conversely, because of rounding, the error may fail to result even when the problem does have multiple solutions.
Example 1
A straight line fit to a data set is computed under the LAV criterion.
#include <imsls.h>
#include <stdio.h>
int main()
{
float xx[] = {1.0, 4.0, 2.0, 2.0, 3.0, 3.0, 4.0, 5.0};
float yy[] = {1.0, 5.0, 0.0, 2.0, 1.5, 2.5, 2.0, 3.0};
float sea;
int irank, iter, nrmiss;
float *coefficients = NULL;
coefficients = imsls_f_Lnorm_regression(8, 1, xx, yy,
IMSLS_SEA, &sea,
IMSLS_RANK, &irank,
IMSLS_ITERATIONS, &iter,
IMSLS_N_ROWS_MISSING, &nrmiss,0);
printf("B = %6.2f\t%6.2f\n\n", coefficients[0], coefficients[1]);
printf("Rank of Regressors Matrix = %3d\n", irank);
printf("Sum Absolute Value of Error = %8.4f\n", sea);
printf("Number of Iterations = %3d\n", iter);
printf("Number of Rows Missing = %3d\n", nrmiss);
}
Output
B = 0.50 0.50
Rank of Regressors Matrix = 2
Sum Absolute Value of Error = 6.00000
Number of Iterations = 2
Number of Rows Missing = 0
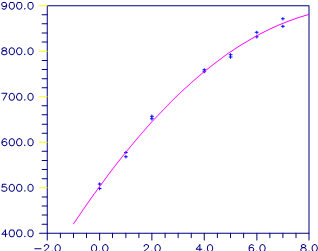
Figure 2-2 Least Squares and Least Absolute Value Fitted Lines
Example 2
Different straight line fits to a data set are computed under the criterion of minimizing the Lp norm by using p equal to 1, 1.5, 2.0 and 2.5.
#include <imsls.h>
#include <stdio.h>
int main()
{
float xx[] = {1.0, 4.0, 2.0, 2.0, 3.0, 3.0, 4.0, 5.0};
float yy[] = {1.0, 5.0, 0.0, 2.0, 1.5, 2.5, 2.0, 3.0};
float p, tolerance, convergence_eps, square_of_scale, df_error;
float Lp_norm_residual;
float R_matrix[4], residuals[8];
float *coefficients = NULL;
int i, irank, iter, nrmiss;
int n_row=2;
int n_col=2;
char *dashes=
"---------------------------------------------------------";
tolerance = 100*imsls_f_machine(4);
convergence_eps = 0.001;
p = 1.0;
for(i=0; i<4; i++)
{
coefficients = imsls_f_Lnorm_regression(8, 1, xx, yy,
IMSLS_METHOD_LLP, p,
IMSLS_EPS, convergence_eps,
IMSLS_RANK, &irank,
IMSLS_ITERATIONS, &iter,
IMSLS_N_ROWS_MISSING, &nrmiss,
IMSLS_R_USER, R_matrix,
IMSLS_DEGREES_OF_FREEDOM, &df_error,
IMSLS_RESIDUALS_USER, residuals,
IMSLS_SCALE, &square_of_scale,
IMSLS_RESIDUALS_LP_NORM, &Lp_norm_residual,
0);
printf("Coefficients = %6.2f\t%6.2f\n\n", coefficients[0],
coefficients[1]);
printf("Residuals = %6.2f\t%6.2f\t%6.2f\t%6.2f\n",
residuals[0], residuals[1], residuals[2], residuals[3]);
printf("\t%6.2f\t%6.2f\t%6.2f\t%6.2f\n\n",
residuals[4], residuals[5], residuals[6], residuals[7]);
printf("P = %5.3f\n", p);
printf("Lp norm of the residuals = %5.3f\n", Lp_norm_residual);
printf("Rank of Regressors Matrix = %3d\n", irank);
printf("Degrees of Freedom Error = %5.3f\n", df_error);
printf("Number of Iterations = %3d\n", iter);
printf("Number of Missing Values = %3d\n", nrmiss);
printf("Square of Scale Constant = %5.3f\n", square_of_scale);
imsls_f_write_matrix("R Matrix\n", n_row, n_col, R_matrix, 0);
printf("%s\n\n", dashes);
p += 0.5;
}
}
Output
Coefficients = 0.50 0.50
Residuals = -0.00 2.50 -1.50 0.50
-0.50 0.50 -0.50 -0.00
P = 1.000
Lp norm of the residuals = 6.002
Rank of Regressors Matrix = 2
Degrees of Freedom Error = 6.000
Number of Iterations = 8
Number of Missing Values = 0
Square of Scale Constant = 6.248
R Matrix
1 2
1 2.828 8.485
2 0.000 3.464
---------------------------------------------------------
Coefficients = 0.39 0.56
Residuals = 0.06 2.39 -1.50 0.50
-0.55 0.45 -0.61 -0.16
P = 1.500
Lp norm of the residuals = 3.712
Rank of Regressors Matrix = 2
Degrees of Freedom Error = 6.000
Number of Iterations = 6
Number of Missing Values = 0
Square of Scale Constant = 1.059
R Matrix
1 2
1 2.828 8.485
2 0.000 3.464
---------------------------------------------------------
Coefficients = -0.13 0.75
Residuals = 0.38 2.13 -1.38 0.63
-0.63 0.38 -0.88 -0.63
P = 2.000
Lp norm of the residuals = 2.937
Rank of Regressors Matrix = 2
Degrees of Freedom Error = 6.000
Number of Iterations = 1
Number of Missing Values = 0
Square of Scale Constant = 1.438
R Matrix
1 2
1 2.828 8.485
2 0.000 3.464
---------------------------------------------------------
Coefficients = -0.44 0.87
Residuals = 0.57 1.96 -1.30 0.70
-0.67 0.33 -1.04 -0.91
P = 2.500
Lp norm of the residuals = 2.540
Rank of Regressors Matrix = 2
Degrees of Freedom Error = 6.000
Number of Iterations = 4
Number of Missing Values = 0
Square of Scale Constant = 0.789
R Matrix
1 2
1 2.828 8.485
2 0.000 3.464
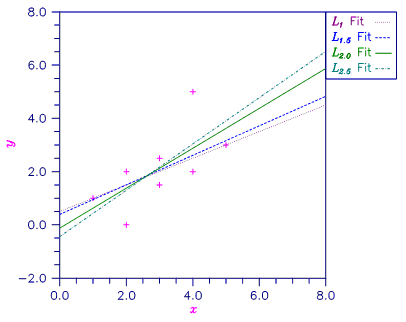
Figure 2-3 Various Lp Fitted Lines
Example 3
A straight line fit to a data set is computed under the LMV criterion.
#include <imsls.h>
#include <stdio.h>
int main()
{
float xx[] = {0.0, 1.0, 2.0, 3.0, 4.0, 4.0, 5.0};
float yy[] = {0.0, 2.5, 2.5, 4.5, 4.5, 6.0, 5.0};
float max_residual;
int irank, iter, nrmiss;
float *coefficients = NULL;
coefficients = imsls_f_Lnorm_regression(7, 1, xx, yy,
IMSLS_METHOD_LMV,
IMSLS_MAX_RESIDUAL, &max_residual,
IMSLS_RANK, &irank,
IMSLS_ITERATIONS, &iter,
IMSLS_N_ROWS_MISSING, &nrmiss,
0);
printf("B = %6.2f\t%6.2f\n\n", coefficients[0], coefficients[1]);
printf("Rank of Regressors Matrix = %3d\n", irank);
printf("Magnitude of Largest Residual = %8.4f\n", max_residual);
printf("Number of Iterations = %3d\n", iter);
printf("Number of Rows Missing = %3d\n", nrmiss);
}
Output
B = 1.00 1.00
Rank of Regressors Matrix = 2
Magnitude of Largest Residual = 1.00000
Number of Iterations = 3
Number of Rows Missing = 0
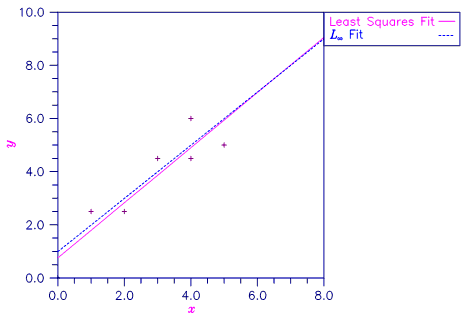
Figure 2-4 Least Squares and Least Maximum Value Fitted Lines
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |