normal_one_sample

Chapter 1: Basic Statistics

normal_one_sample

Computes statistics for mean and variance inferences using a sample from a normal population.

Synopsis

#include <imsls.h>

float imsls_f_normal_one_sample (int n_observations, float x[], ..., 0)

The type double function is imsls_d_normal_one_sample.

Required Arguments

int n_observations (Input)
Number of observations.

float x[] (Input)
Array of length n_observations.

Return Value

The mean of the sample.

Synopsis with Optional Arguments

#include <imsls.h>

float imsls_f_normal_one_sample (int n_observations, float x[],
IMSLS_CONFIDENCE_MEAN, float confidence_mean,
IMSLS_CI_MEAN, float *lower_limit, float *upper_limit,
IMSLS_STD_DEV, float *std_dev,
IMSLS_T_TEST, int *df, float *t, float *p_value,
IMSLS_T_TEST_NULL, float mean_hypothesis_value,
IMSLS_CONFIDENCE_VARIANCE, float confidence_variance,
IMSLS_CI_VARIANCE, float *lower_limit, float *upper_limit,
IMSLS_CHI_SQUARED_TEST, int *df, float *chi_squared, float *p_value,
IMSLS_CHI_SQUARED_TEST_NULL, float variance_hypothesis_value,
0)

Optional Arguments

IMSLS_CONFIDENCE_MEAN, float confidence_mean (Input)
Confidence level (in percent) for two-sided interval estimate of the mean. Argument confidence_mean must be between 0.0 and 100.0 and is often 90.0, 95.0, or 99.0. For a one-sided confidence interval with confidence level c (at least 50 percent), set confidence_mean = 100.0 − 2.0 × (100.0 − c). If IMSLS_CONFIDENCE_MEAN is not specified, a 95-percent confidence interval is computed.

IMSLS_CI_MEAN, float *lower_limit, float *upper_limit (Output)
Argument lower_limit contains the lower confidence limit for the mean, and argument upper_limit contains the upper confidence limit for the mean.

IMSLS_STD_DEV, float *std_dev (Output)
Standard deviation of the sample.

IMSLS_T_TEST, int *df, float *t, float *p_value (Output)
Argument df is the degrees of freedom associated with the t test for the mean, t is the test statistic, and p_value is the probability of a larger
t in absolute value. The t test is a test, against a two-sided alternative, of the hypothesis μ = μ0, where μ0 is the null hypothesis value as described in IMSLS_T_TEST_NULL.

IMSLS_T_TEST_NULL, float mean_hypothesis_value (Input)
Null hypothesis value for t test for the mean.
Default: mean_hypothesis_value = 0.0

IMSLS_CONFIDENCE_VARIANCE, float confidence_variance (Input)
Confidence level (in percent) for two-sided interval estimate of the variances. Argument confidence_variance must be between 0.0 and 100.0 and is often 90.0, 95.0, 99.0. For a one-sided confidence interval with confidence level c (at least 50 percent), set confidence_variance = 100.0 − 2.0 × (100.0 − c). If this option is not used, a 95-percent confidence interval is computed.

IMSLS_CI_VARIANCE, float *lower_limit, float *upper_limit (Output)
Contains the lower and upper confidence limits for the variance.

IMSLS_CHI_SQUARED_TEST, int *df, float *chi_squared, float *p_value (Output)
Argument df is the degrees of freedom associated with the chi-squared test for variances, chi_squared is the test statistic, and p_value is the probability of a larger chi-squared. The chi-squared test is a test of the hypothesis

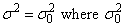
is the null hypothesis value as described in IMSLS_CHI_SQUARED_TEST_NULL.

IMSLS_CHI_SQUARED_TEST_NULL, float variance_hypothesis_value (Input)
Null hypothesis value for the chi-squared test.
Default: variance_hypothesis_value = 1.0

Description

Statistics for mean and variance inferences using a sample from a normal population are computed, including confidence intervals and tests for both mean and variance. The definitions of mean and variance are given below. The summation in each case is over the set of valid observations, based on the presence of missing values in the data.

Mean, return value

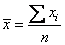
Standard deviation, std_dev

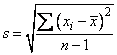
The t statistic for the two-sided test concerning the population mean is given by

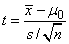
where s and 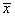are given above. This quantity has a T distribution with n − 1 degrees of freedom.

The chi-squared statistic for the two-sided test concerning the population variance is given by

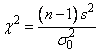
where s is given above. This quantity has a Χ2 distribution with n − 1 degrees of freedom.

Examples

Example 1

This example uses data from Devore (1982, p. 335), which is based on data published in the Journal of Materials. There are 15 observations; the mean is the only output.

#include <imsls.h>

int main()

{

#define N_OBSERVATIONS 15

float mean;

float x[N_OBSERVATIONS] = {

26.7, 25.8, 24.0, 24.9, 26.4,

25.9, 24.4, 21.7, 24.1, 25.9,

27.3, 26.9, 27.3, 24.8, 23.6};

/* Perform analysis */

mean = imsls_f_normal_one_sample(N_OBSERVATIONS, x, 0);

/* Print results */

printf("Sample Mean = %5.2f", mean);

}

Output

Sample Mean = 25.3

Example 2

This example uses the same data as the initial example. The hypothesis H0: μ = 20.0 is tested. The extremely large t value and the correspondingly
small p-value provide strong evidence to reject the null hypothesis.

#include <imsls.h>

main()

{

#define N_OBSERVATIONS 15

int df;

float mean, s, lower_limit, upper_limit, t, p_value;

static float x[N_OBSERVATIONS] = {

26.7, 25.8, 24.0, 24.9, 26.4,

25.9, 24.4, 21.7, 24.1, 25.9,

27.3, 26.9, 27.3, 24.8, 23.6};

/* Perform analysis +*/

mean = imsls_f_normal_one_sample(N_OBSERVATIONS, x,

IMSLS_STD_DEV, &s,

IMSLS_CI_MEAN, &lower_limit, &upper_limit,

IMSLS_T_TEST_NULL, 20.0,

IMSLS_T_TEST, &df, &t, &p_value,

0);

/* Print results */

printf("Sample Mean = %5.2f\n", mean);

printf("Sample Standard Deviation = %5.2f\n", s);

printf("95%% CI for the mean is (%5.2f,%5.2f)\n", lower_limit,

upper_limit);

printf("df = %3d\n", df);

printf("t = %5.2f\n", t);

printf("p-value = %8.5f\n", p_value);

}

Output

Sample Mean = 25.31

Sample Standard Deviation = 1.58

95% CI for the mean is (24.44,26.19)

df = 14

t = 13.03

p-value = 0.00000

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260