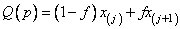Computes empirical quantiles.

Synopsis

#include <imsls.h>

float *imsls_f_empirical_quantiles (int n_observations,  float x[],  
int n_qprop,  float qprop[],  ..., 0)

The type double function is imsls_d_empirical_quantiles.

Required Arguments

int n_observations   (Input)
Number of observations.

float x[](Input)
An array of length n_observations containing the data. 

int n_qprop   (Input)
Number of empirical quantiles requested. 

float qprop[ ]  (Input)
An array of length n_qprop containing the desired quantile proportions.  Each value must lie in the interval (0,1). 

Return Value

The function imsls_f_empirical_quantiles returns an array of length n_qprop containing the empirical quantiles corresponding to the input proportions in qprop.

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_empirical_quantiles(int n_observations,  float x[],  
int n_qprop,  float qprop[],
IMSLS_N_MISSING, int *n_miss,
IMSLS_XLO, float **xlo,
IMSLS_XLO_USER, float  xlo[],
IMSLS_XHI, float **xhi,
IMSLS_XHI_USER, float  xhi[],
IMSLS_RETURN_USER, float  p_q[],
 0)

Optional Arguments

IMSLS_N_MISSING,  int *n_miss (Output)
The number of missing values, if any, in x.

IMSLS_XLO, float **xlo (Output)
An array of length n_qprop containing the largest element of x less than or equal to the desired quantile.

IMSLS_XLO_USER, float xlo[] (Output)
Storage for xlo provided by the user.  See IMSLS_XLO above.

IMSLS_XHI, float **xhi (Output)
An array of length n_qprop containing the smallest element of x greater than or equal to the desired quantile.

IMSLS_XHI_USER, float xhi[]  (Output)
Storage for xhi provided by the user.  See IMSLS_XHI above.

IMSLS_RETURN_USER, float p_q[] (Output)
A user-allocated array of length n_qprop. Upon completion p_q contains the empirical quantiles corresponding to the input proportions in qprop.

Description

The function imsls_f_empirical_quantiles determines the empirical quantiles, as indicated in the vector qprop, from the data in x.  imsls_f_empirical_quantiles first checks to see if x is sorted; if x is not sorted, the routine does either a complete or partial sort, depending on how many order statistics are required to compute the quantiles requested.

This function returns the empirical quantiles and, for each quantile, the two order statistics from the sample that are at least as large and at least as small as the quantile. For a sample of size n, the quantile corresponding to the proportion p is defined as

where j = ⌊p(n + 1)⌋, f = p(n + 1) − j, and x(j) is the j-th order statistic, if 1 ≤ j < n; otherwise, the empirical quantile is the smallest or largest order statistic.

Example

In this example, five empirical quantiles from a sample of size 30 are obtained. Notice that the 0.5 quantile corresponds to the sample median. The data are from Hinkley (1977) and Velleman and Hoaglin (1981). They are the measurements (in inches) of precipitation in Minneapolis/St. Paul during the month of March for 30 consecutive years.

#include <imsls.h>

#include <stdio.h>

int main(){

       float x[30] = {

              0.77, 1.74, 0.81, 1.20, 1.95,

              1.20, 0.47, 1.43, 3.37, 2.20,

              3.00, 3.09, 1.51, 2.10, 0.52,

              1.62, 1.31, 0.32, 0.59, 0.81,

              2.81, 1.87, 1.18, 1.35, 4.75,

              2.48, 0.96, 1.89, 0.90, 2.05};

       float qprop[5] = {

              0.01, 0.5,  0.9,  0.95, 0.99};

       float *p_xlo, *p_xhi, *p_q;

       int i;

      

       p_q = imsls_f_empirical_quantiles(30, x, 5, qprop,

                     IMSLS_XLO, &p_xlo,

IMSLS_XHI, &p_xhi,

0);

 

       printf("          Smaller  Empirical  Larger\n");

       printf("Quantile   Datum    Quantile   Datum\n");

       for(i=0; i<5; i++){

              printf("  %4.2f   %7.2f   %7.2f   %7.2f\n",

              qprop[i], p_xlo[i], p_q[i], p_xhi[i]);

       }

}

Output

 

          Smaller  Empirical  Larger

Quantile   Datum    Quantile   Datum

  0.01      0.32      0.32      0.32

  0.50      1.43      1.47      1.51

  0.90      3.00      3.08      3.09

  0.95      3.37      3.99      4.75

  0.99      4.75      4.75      4.75

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260