randomness

Chapter 7: Tests of Goodness of Fit

randomness_test

Performs a test for randomness.

Synopsis

#include <imsls.h>

float imsls_f_randomness_test (int n_observations, float x[],
int n_run..., 0)

The type double function is imsls_d_randomness_test.

Required Arguments

int n_observations (Input)
Number of observations in x.

float x[] (Input)
Array of size n_observations containing the data.

int n_run (Input)
Length of longest run for which tabulation is desired. For optional arguments IMSLS_PAIRS, IMSLS_DSQUARE, and IMSLS_DCUBE, n_run stands for the number of equiprobable cells into which the statistics are to be tabulated.

Return Value

The probability of a larger chi-squared statistic for testing the null hypothesis of a uniform distribution.

Synopsis with Optional Arguments

#include <imsls.h>

float imsls_f_randomness_test (int n_observations, float x[], int n_run,
IMSLS_RUNS, float **runs_count, float **covariances,
IMSLS_RUNS_USER , float runs_count[], float covariances[],
IMSLS_PAIRS, int pairs_lag, float **pairs_count,
IMSLS_PAIRS_USER, int pairs_lag, float pairs_count[],
IMSLS_DSQUARE, float **dsquare_count,
IMSLS_DSQUARE_USER, float dsquare_count[],
IMSLS_DCUBE, float **dcube_count,
IMSLS_DCUBE_USER, float dcube_count[],
IMSLS_RUNS_EXPECT, float **runs_expect,
IMSLS_RUNS_EXPECT_USER, float runs_expect[],
IMSLS_EXPECT, float *expect,
IMSLS_CHI_SQUARED, float *chi_squared,
IMSLS_DF, float *df,
IMSLS_RETURN USER, float *pvalue,
0)

Optional Arguments

IMSLS_RUNS, float **runs_count, float **covariances, (Output) or

IMSLS_PAIRS, int pairs_lag (Input), float **pairs_count,(Output) or

IMSLS_DSQUARE, float **dsquare_count, (Output) or

IMSLS_DCUBE, float **dcube_count, (Output)

IMSLS_RUNS indicates the runs test is to be performed. Array of length n_run containing the counts of the number of runs up of each length is returned in runs_counts. n_run by n_run matrix containing the variances and covariances of the counts is returned in covariances. IMSLS_RUNS is the default test, however, to return the counts and covariances IMSLS_RUNS argument must be used.

IMSLS_PAIRS indicates the pairs test is to be performed. The lag to be used in computing the pairs statistic is stored in pairs_lag. Pairs (X[i], X[i + pairs_lag]) for i = 0,…, N – pairs_lag -1 are tabulated, where N is the total sample size. n_run by n_run matrix containing the count of the number of pairs in each cell is returned in pairs_user.

IMSLS_DSQUARE indicates the d² test is to be performed. dsquare_counts is an address of a pointer to an internally allocated array of length n_run containing the tabulations for the d² test.

IMSLS_DCUBE indicates the triplets test is to be performed. dcube_counts is an address of a pointer to an internally allocated array of length n_run by n_run by n_run containing the tabulations for the triplets test.

IMSLS_RUNS_USER, float runs_counts[], float covariances[] (Output)
Storage for runs_counts and covariances is provided by the user. See IMSLS_RUNS.

IMSLS_PAIRS_USER, int pairs_lag, float pairs_counts[] (Output)
Storage for pairs_lag and pairs_counts is provided by the user. See IMSLS_PAIRS.

IMSLS_DSQUARE_USER, float dsquare_count[] (Output)
Storage for dsquare_count is provided by the user.
See IMSLS_DSQUARE.

IMSLS_DCUBE_USER, float dcube_count[] (Output)
Storage for dcube_count is provided by the user. See IMSLS_DCUBE.

IMSLS_CHI_SQUARED, float *chi_squared (Output)
Chi-squared statistic for testing the null hypothesis of a uniform distribution.

IMSLS_DF, float *df (Output)
Degrees of freedom for chi-squared.

IMSLS_RETURN_USER, float *pvalue (Output)
If specified, pvalue returns the probability of a larger chi-squared statistic for testing the null hypothesis of a uniform distribution.

If IMSLS_RUNS is specified:

IMSLS_RUNS_EXPECT, float **runs_expect (Output)
The address of a pointer to an internally allocated array of length
n_run containing the expected number of runs of each length.

IMSLS_RUNS_EXPECT_USER, float runs_expect[] (Output)
Storage for runs_expect is provided by the user.
See IMSLS_RUNS_EXPECT.

If IMSLS_PAIRS, IMSLS_DSQUARE, or IMSLS_DCUBE is specified:

IMSLS_EXPECT, float **expect (Output)
Expected number of counts for each cell. This argument is optional only if one of IMSLS_PAIRS, IMSLS_DSQUARE, or IMSLS_DCUBE is used.

Description

Runs Up Test

Function imsls_f_randomness_test performs one of four different tests for randomness. Optional argument IMSLS_RUNS computes statistics for the runs up test. Runs tests are used to test for cyclical trend in sequences of random numbers. If the runs down test is desired, each observation should first be multiplied by -1 to change its sign, and IMSLS_RUNS called with the modified vector of observations.

IMSLS_RUNS first tallies the number of runs up (increasing sequences) of each desired length. For i = 1, K, r - 1, where r = n_run, runs_count[i] contains the number of runs of length i. runs_count[n_run] contains the number of runs of length n_run or greater. As an example of how runs are counted, the sequence (1, 2, 3, 1) contains 1 run up of length 3, and one run up of length 1.

After tallying the number of runs up of each length, IMSLS_RUNS computes the
expected values and the covariances of the counts according to methods given by Knuth (1981, pages 65-67). Let R denote a vector of length n_run containing the number of runs of each length so that the i-th element of R, ri, contains the count of the runs of length i. Let SR denote the covariance matrix of R under the null hypothesis of randomness, and let mR denote the vector of expected values for R under this null hypothesis, then an approximate chi-squared statistic with n_run degrees of freedom is given as

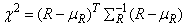
In general, the larger the value of each element of mR, the better the chi-squared approximation.

Pairs Test

IMSLS_PAIRS computes the pairs test (or the Good's serial test) on a hypothesized sequence of uniform (0,1) pseudorandom numbers. The test proceeds as follows. Subsequent pairs (X(i), X(i + pairs_lag)) are tallied into a k ´ k matrix, where
k = n_run. In this tally, element (j, m) of the matrix is incremented, where

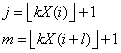
where l = pairs_lag, and the notation ë û represents the greatest integer function, ëYû is the greatest integer less than or equal to Y, where Y is a real number. If l = 1, then
i = 1, 3, 5, K, n - 1. If l > 1, then i = 1, 2, 3, ¼, n - l, where n is the total number of pseudorandom numbers input on the current invocation of IMSLS_pAIRS
(i.e., n = n_observations).

Given the tally matrix in pairs_count, chi-squared is computed as

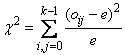
where e = åoij/k2, and oij is the observed count in cell (i, j) (oij = pairs_count(i, j)).

Because pair statistics for the trailing observations are not tallied on any call, the user should call IMSLS_PAIRS with n_observations as large as possible. For pairs_lag < 20 and n_observations = 2000, little power is lost.

d ² Test

IMSLS_DSQAR computes the d2 test for succeeding quadruples of hypothesized pseudorandom uniform (0, 1) deviates. The d2 test is performed as follows. Let X_, X₂, X₃, and X₄denote four pseudorandom uniform deviates, and consider

D2 = (X3 -X1)2 + (X4 - X2)2

The probability distribution of D2 is given as

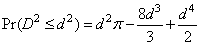
when D2 ≤ 1, where p denotes the value of pi. If D2 > 1, this probability is given as

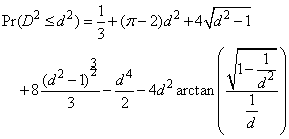
See Gruenberger and Mark (1951) for a derivation of this distribution.

For each succeeding set of 4 pseudorandom uniform numbers input in X, d2 and the cumulative probability of d2 (Pr(D2 £ d2)) are computed. The resulting probability is tallied into one of k = n_run equally spaced intervals.

Let n denote the number of sets of four random numbers input (n = the total number of observations/4). Then, under the null hypothesis that the numbers input are random uniform (0, 1) numbers, the expected value for each element in dsquare_count is
e = n/k. An approximate chi-squared statistic is computed as

where oi = dsquare_count(i) is the observed count. Thus, c2 has k - 1 degrees of freedom, and the null hypothesis of pseudorandom uniform (0, 1) deviates is rejected if c2 is too large. As n increases, the chi-squared approximation becomes better. A useful generalization is that e > 5 yields a good chi-squared approximation.

Triplets Test

IMSLS_DCUBE computes the triplets test on a sequence of hypothesized pseudorandom uniform(0, 1) deviates. The triplets test is computed as follows:

Each set of three successive deviates, X1, X2, and X3, is tallied into one of m3 equal sized cubes, where m = n_run. Let i = [mX1] + 1, j = [mX2] + 1, and
k = [mX3] + 1. For the triplet (X1, X2, X3), dcube_count(i, j, k) is incremented.

Under the null hypothesis of pseudorandom uniform(0, 1) deviates, the m3 cells are equally probable and each has expected value e = n/m3, where n is the number of triplets tallied. An approximate chi-squared statistic is computed as

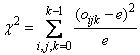
where oijk = dcube_count(i, j, k).

The computed chi-squared has m3 - 1 degrees of freedom, and the null hypothesis of pseudorandom uniform (0, 1) deviates is rejected if c2 is too large.

Examples

Example 1

This example illustrates the use of the runs test on 104 pseudo-random uniform deviates. In the example, 2000 deviates are generated for each call to IMSLS_RUNS. Since the probability of a larger chi-squared statistic is 0.1872, there is no strong evidence to support rejection of this null hypothesis of randomness.

#include <imsls.h>

#include <stdio.h>

int main()

{

int nran = 10000, n_run = 6;

char *fmt = "%8.1f";

float *x, pvalue, *runs_counts, *runs_expect, chisq, df;

imsls_random_seed_set(123457);

x = imsls_f_random_uniform(nran, 0);

pvalue = imsls_f_randomness_test(nran, x, n_run,

IMSLS_CHI_SQUARED, &chisq,

IMSLS_DF, &df,

IMSLS_RUNS_EXPECT, &runs_expect,

IMSLS_RUNS, &runs_counts, &covariances,

0);

imsls_f_write_matrix("runs_counts", 1, n_run, runs_counts, 0);

imsls_f_write_matrix("runs_expect", 1, n_run, runs_expect,

IMSLS_WRITE_FORMAT, fmt,

0);

imsls_f_write_matrix("covariances", n_run, n_run, covariances,

IMSLS_WRITE_FORMAT, fmt,

0);

printf("chisq = %f\n", chisq);

printf("df = %f\n", df);

printf("pvalue = %f\n", pvalue);

}

Output

runs_count

1 2 3 4 5 6

1709.0 2046.0 953.0 260.0 55.0 4.0

runs_expect

1 2 3 4 5 6

1667.3 2083.4 916.5 263.8 57.5 11.9

Covariances

1 2 3 4 5 6

1 1278.2 -194.6 -148.9 -71.6 -22.9 -6.7

2 -194.6 1410.1 -490.6 -197.2 -55.2 -14.4

3 -148.9 -490.6 601.4 -117.4 -31.2 -7.8

4 -71.6 -197.2 -117.4 222.1 -10.8 -2.6

5 -22.9 -55.2 -31.2 -10.8 54.8 -0.6

6 -6.7 -14.4 -7.8 -2.6 -0.6 11.7

chisq = 8.76514

df = 6.00000

pvalue = 0.187225

Example 2

This example illustrates the calculations of the IMSLS_pAIRS statistics when a random sample of size 104 is used and the pairs_lag is 1. The results are not significant. IMSL routine imsls_f_random_uniform (Chapter 12, “Random Number) is used in obtaining the pseudorandom deviates.

#include <imsls.h>

#include <stdio.h>

int main()

{

int nran = 10000, n_run = 10;

float *x, pvalue, *pairs_counts, expect, chisq, df;

imsls_random_seed_set(123467);

x = imsls_f_random_uniform(nran, 0);

pvalue = imsls_f_randomness_test(nran, x, n_run,

IMSLS_CHI_SQUARED, &chisq,

IMSLS_DF, &df,

IMSLS_EXPECT, &expect,

IMSLS_PAIRS, 5, &pairs_counts,

0);

imsls_f_write_matrix("pairs_counts", n_run, n_run, pairs_counts, 0);

printf("expect = %8.2f\n", expect);

printf("chisq = %8.2f\n", chisq);

printf("df = %8.2f\n", df);

printf("pvalue = %10.4f\n", pvalue);

}

Output

pairs_counts

1 2 3 4 5 6 7 8 9 10

1 112 82 95 118 103 103 113 84 90 74

2 104 106 109 108 101 98 102 92 109 88

3 88 111 86 106 112 79 103 105 106 101

4 91 110 108 92 88 108 113 93 105 114

5 104 105 103 104 101 94 96 87 93 104

6 98 104 103 104 79 89 92 104 92 100

7 103 91 97 101 116 83 118 118 106 99

8 105 105 111 91 93 82 100 104 110 89

9 92 102 82 101 94 128 102 110 125 98

10 79 99 103 98 104 101 93 93 98 105

expect = 99.95

chisq = 104.86

df = 99.00

pvalue = 0.3242

Example 3

In this example, 2000 observations generated via IMSL routine imsls_f_random_uniform (Chapter 12, “Random Number Generation”) are input to IMSLS_DSQAR in one call. In the example, the null hypothesis of a uniform distribution is not rejected.

#include <imsls.h>

#include <stdio.h>

int main()

{

int nran = 2000, n_run = 6;

float *x, pvalue, *dsquare_counts, *covariances, expect, chisq, df;

imsls_random_seed_set(123457);

x = imsls_f_random_uniform(nran, 0);

pvalue = imsls_f_randomness_test(nran, x, n_run,

IMSLS_CHI_SQUARED, &chisq,

IMSLS_DF, &df,

IMSLS_EXPECT, &expect,

IMSLS_DSQUARE, &dsquare_counts,

0);

imsls_f_write_matrix("dsquare_counts", 1, n_run, dsquare_counts, 0);

printf("expect = %10.4f\n", expect);

printf("chisq = %10.4f\n", chisq);

printf("df = %8.2f\n", df);

printf("pvalue = %10.4f\n", pvalue);

}

Output

dsquare_counts

1 2 3 4 5 6

87 84 78 76 92 83

expect = 83.3333

chisq = 2.0560

df = 5.00

pvalue = 0.8413

Example 4

In this example, 2001 deviates generated by IMSL routine imsls_f_random_uniform (Chapter 12, “Random Number Generation”) are input to IMSLS_DCUBE, and tabulated in 27 equally sized cubes. In the example, the null hypothesis is not rejected.

#include <imsls.h>

#include <stdio.h>

int main()

{

int nran = 2001, n_run = 3;

float *x, pvalue, *dcube_counts, expect, chisq, df;

imsls_random_seed_set(123457);

x = imsls_f_random_uniform(nran, 0);

pvalue = imsls_f_randomness_test(nran, x, n_run,

IMSLS_CHI_SQUARED, &chisq,

IMSLS_DF, &df,

IMSLS_EXPECT, &expect,

IMSLS_DCUBE, &dcube_counts,

0);

imsls_f_write_matrix("dcube_counts", n_run, n_run, dcube_counts, 0);

imsls_f_write_matrix("dcube_counts", n_run, n_run,

&dcube_counts[n_run*n_run], 0);

imsls_f_write_matrix("dcube_counts", n_run, n_run,

&dcube_counts[2*n_run*n_run], 0);

printf("expect = %10.4f\n", expect);

printf("chisq = %10.4f\n", chisq);

printf("df = %8.2f\n", df);

printf("pvalue = %10.4f\n", pvalue);

}

Output

dcube_counts

1 2 3

1 26 27 24

2 20 17 32

3 30 18 21

dcube_counts

1 2 3

1 20 16 26

2 22 22 27

3 30 24 26

dcube_counts

1 2 3

1 28 30 22

2 23 24 22

3 33 30 27

expect = 24.7037

chisq = 21.7631

df = 26.0000

pvalue = 0.701586

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260

randomness_test

Synopsis

Required Arguments

Return Value

The probability of a larger chi-squared statistic for testing the null hypothesis of a uniform distribution.

Synopsis with Optional Arguments

Optional Arguments

Description

Runs Up Test

Pairs Test

d 2 Test

Triplets Test

Examples

Example 1

Output

Example 2

Output

Example 3

Output

Example 4

Output

d ² Test