Solves an initial-value problem for a system of ordinary differential equations of order one or two using a variable order Adams method.
Synopsis
#include <imsl.h>
void imsl_f_ode_adams_2nd_order (int neq, float *t, float tend, int *ido, float y[], float hidrvs[], void fcn(), ..., 0)
The type double function is imsl_d_ode_adams_2nd_order.
Required Arguments
int neq
(Input)
Number of differential equations in the system of equations to
solve.
float *t
(Input/Output)
On input, t contains the initial
independent variable value. On output, t is replaced by tend unless error
conditions arise. See ido for details.
float tend
(Input)
Value of t = tend where the solution is
required.
int *ido
(Input/Output)
Flag indicating the state of the computation.
|
ido |
State |
|
1 |
Initial entry input value. |
|
2 |
Normal re-entry input value. On output, if ido = 2 then the integration is finished. If the integrator is called with a new value for tend, the integration continues. If the integrator is called with tend unchanged, an error message is issued. |
|
3 |
Input value to use on final call to release workspace. |
|
>3 |
Output value that indicates that a fatal error has occurred. |
The initial call is made with ido = 1. The function then sets ido = 2, and this value is used for all but the last call that is made with ido = 3. This final call is only used to release workspace which was automatically allocated by the initial call with ido = 1.
float y[] (Input/Output)
An array of length
k containing the dependent variables, y(t), and first
derivatives, if any. k will be the sum of the orders of the
equations in the system of equations to solve, that is, the sum of the elements
of korder. On
input, y
contains the initial values, y(t0) and y’(t0) (if needed).
On output, y contains the
approximate solution, y(t). For example, for a system of first
order equations, y[i-1] is the
i-th
dependent variable. For a system of second order equations, y[2i-2] is the
i-th
dependent variable and y[2i-1] is the
derivative of the i-th dependent
variable. For systems of equations in which one or more equations is of order 2,
optional argument IMSL_EQ_ORDER must be
used to denote the order of each equation so that the derivatives in y can be identified.
By default it is assumed that all equations are of order 1 and y contains only
dependent variables.
float hidrvs[] (Output)
An array of length neq containing the
highest order derivatives at the point y.
void fcn
(int neq,
int ido,
float t,
float y[],
float hidrvs) (Input)
User-supplied function to
evaluate derivatives.
Arguments
int neq
(Input)
Number of differential equations in the system of equations to
solve.
int ido
(Input)
Flag indicating the state of the computation. This flag corresponds
to the ido
argument described above. If fcn has complicated
subexpressions, which depend only weakly or not at all on y then these
subexpressions need only be computed when ido = 1 and
their values then reused when ido = 2.
float t (Input)
Independent variable,
t.
float y[]
(Input)
An array of length k containing the dependent variable
values, y, and first derivatives, if any. k will be the sum of the
orders of the equations in the system of equations to solve.
float hidrvs[] (Output)
An array of length neq containing the
values of the highest order derivatives evaluated at
(t, y).
Synopsis with Optional Arguments
#include <imsl.h>
void imsl_f_ode_adams_2nd_order (int neq, float *t, float tend, int *ido, float y[], float hidrvs[], void fcn(),
IMSL_EQ_ORDER, int korder[],
IMSL_EQ_ERR, float eqnerr[],
IMSL_STEPSIZE_INC, float hinc,
IMSL_STEPSIZE_DEC, float hdec,
IMSL_MIN_STEPSIZE, float hmin,
IMSL_MAX_STEPSIZE, float hmax,
IMSL_FCN_W_DATA, void fcn(), void *data,
0)
Optional Arguments
IMSL_EQ_ORDER,
int korder[]
(Input)
An array of length neq specifying the
orders of the equations in the system of equations to solve. The elements of
korder can be 1
or 2. korder
must be used with argument y to define systems of
mixed or higher order.
Default: korder = [1,1,1,...,1].
IMSL_EQ_ERR,
float eqnerr[]
(Input)
An array of length neq specifying the
error tolerance for each equation. Let e(i) be the error tolerance for
equation i for for i = 0,…, neq -1.
Then
|
Value |
Explanation |
|
e(i) > 0 |
Implies an absolute error tolerance of e(i) is to be used for equation i. |
|
e(i) = 0 |
Implies no error checking is to be performed for equation i. |
|
e(i) < 0 |
Implies a relative error test is to be performed for equation i. In this case, the base error tolerance used will be |e(i)| and the relative error factor used will be (15/16 * |e(i)|). Thus the actual absolute error tolerance used will be |e(i)|*(15/16*|e(i)|). |
Default: An absolute error tolerance of 1.e-5 is used for single precision and 1.e-10 for double precision for all equations.
IMSL_STEPSIZE_INC,
float hinc (Input)
Factor
used for increasing the stepsize. One should set hinc such that
9/8 <= hinc <= 4.
Default:
hinc = 2.0.
IMSL_STEPSIZE_DEC,
float hdec (Input)
Factor
used for decreasing the stepsize. One should set hdec such that
1/4 <= hdec <= 7/8.
Default:
hdec = 0.5.
IMSL_MIN_STEPSIZE,
float hmin
(Input)
Absolute value of the minimum stepsize permitted.
Default:
hmin = 10.0/imsl_f_machine(2).
IMSL_MAX_STEPSIZE,
float hmax
(Input)
Absolute value of the maximum stepsize permitted.
Default:
hmax = imsl_f_machine(2).
IMSL_FCN_W_DATA,
void fcn(int neq,
int ido,
float t,
float y[],
float hidrvs[],
void *data),
void *data
(Input)
User-supplied function to evaluate functions, which also accepts a
pointer to data that is supplied by the user. data is a pointer to
the data to be passed to the user-supplied function. Please refer to fcn in the
Required Arguments section for more information. See the Introduction, Passing Data to
User-Supplied Functions at the beginning of this manual for more
details.
Description
imsl_f_ode_adams_2nd_order is based on the JPL Library routine SIVA. imsl_f_ode_adams_2nd_order uses a variable order Adams method to solve the initial value problem
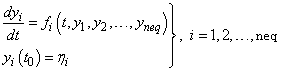
or more generally
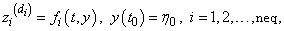
where y is the vector
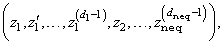
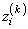 is the kth
derivative of zi with respect to
t, di is the order of the
ith differential equation, and
η is a vector with the same dimension as y.
is the kth
derivative of zi with respect to
t, di is the order of the
ith differential equation, and
η is a vector with the same dimension as y.
Note that the systems of equations solved by imsl_f_ode_adams_2nd_order can be of order one, order two, or mixed order one and two.
Examples
Example 1
In this example a system of two equations of order two is solved.
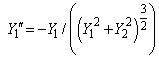
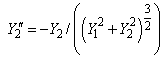
The initial conditions are
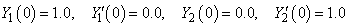
Since the system is of order two, optional argument imsl_eq_order must be used to specify the orders of the equations. Also, because the system is of order two, y[0] contains the first dependent variable, y[1] contains the derivative of the first dependent variable, y[2] contains the second dependent variable, and y[3] contains the derivative of the second dependent variable.
#include <imsl.h>
#include <math.h>
#include <stdio.h>
#define NEQ 2
void fcn(int neq, int ido, float t, float y[], float hidrvs[]);
int main() {
int iend, ido, k, korder[NEQ];
float delta, t, tend, y[4], hidrvs[NEQ];
/* Initialize */
ido = 1;
t = 0.0;
y[0] = 1.0;
y[1] = 0.0;
y[2] = 0.0;
y[3] = 1.0;
korder[0] = 2;
korder[1] = 2;
/* Write Title */
printf(" T Y1/Y2 Y1P/Y2P ");
printf("Y1PP/Y2PP\n");
/* Integrate ODE */
iend = 0;
delta = 2.0 * imsl_f_constant("PI",0);
for(k=0;k<5;k++){
iend += 1;
tend = t + delta;
if(tend > 20.0) tend = 20.0;
imsl_f_ode_adams_2nd_order (NEQ, &t, tend, &ido, y, hidrvs, fcn,
IMSL_EQ_ORDER, korder,
0);
if(iend < 5){
printf("%15.4f %15.4f %15.4f %15.4f\n",
t, y[0], y[1], hidrvs[0]);
printf(" %15.4f %15.4f %15.4f\n",
y[2], y[3], hidrvs[1]);
}
/* Finish up */
if (iend == 4) ido = 3;
}
}
void fcn(int neq, int ido, float t, float y[], float hidrvs[])
{
float tp;
tp = y[0] * y[0] + y[2] * y[2];
tp = 1.0e0/(tp * sqrt(tp));
hidrvs[0] = -y[0] * tp;
hidrvs[1] = -y[2] * tp;
}
Output
T
Y1/Y2
Y1P/Y2P Y1PP/Y2PP
6.2832
1.0000 -0.0000
-1.0000
0.0000 1.0000 0.0000
12.5664 1.0000 -0.0000 -1.0000
0.0000 1.0000 -0.0000
18.8496 1.0000 -0.0000 -1.0000
0.0000 1.0000 -0.0000
20.0000 0.4081 -0.9129 -0.4081
0.9129 0.4081 -0.9129
Example 2
This contrived example illustrates how to use imsl_f_ode_adams_2nd_order to solve a system of equations of mixed order.
The height, y(t), of an object of mass m above the surface of the Earth can be modeled using Newton's second law as:
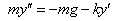
or
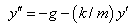 (1)
(1)
where -mg is the downward force of gravity and -ky' is the force due to air resistance, in a direction opposing the velocity. If the object is a meteor, the mass, m, and air resistance, k, will decrease as the meteor burns up in the atmosphere. The mass is proportional to r3 (r = radius) and the air resistance, presumably dependent on the surface area, may be assumed to be proportional to r2, so that k/m = k0/r. The rate at which the meteor’s radius decreases as it burns up may depend on r, on the velocity y', and, since the density of the atmosphere depends on y, on y itself. However, we will construct a very simple model where the rate is just proportional to the square of the velocity,
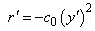 (2)
(2)
We solve (1) and (2), with k0 = 0.005, c0 = 10-8, g = 9.8 and initial conditions y(0) = 100,000 meters, y'(0) = -1000 meters/second, r(0) = 1 meter.
#include <imsl.h>
#include <stdio.h>
#define NEQ 2
void fcn(int neq, int ido, float t, float y[], float hidrvs[]);
int main() {
int iend, ido, k, korder[NEQ];
float delta, t, tend, y[3], eqnerr[NEQ], hidrvs[NEQ];
/* Initialize */
ido = 1;
t = 0.0;
y[0] = 100000.0;
y[1] = -1000.0;
y[2] = 1.0;
korder[0] = 2;
korder[1] = 1;
eqnerr[0] = .003;
eqnerr[1] = .003;
/* Write Title */
printf(" T Y1/Y2 Y1P ");
printf("Y1PP/Y2PP\n");
/* Integrate ODE */
iend = 0;
delta = 10.0;
for(k=0;k<6;k++){
iend += 1;
tend = t + delta;
if(tend > 50.0) tend = 50.0;
imsl_f_ode_adams_2nd_order (NEQ, &t, tend, &ido, y, hidrvs, fcn,
IMSL_EQ_ORDER, korder,
IMSL_EQ_ERR, eqnerr,
0);
if(iend < 6){
printf("%15.4f %15.4f %15.4f %15.4f\n",
t, y[0], y[1], hidrvs[0]);
printf(" %15.4f %15.4f\n",
y[2], hidrvs[1]);
}
/* Finish up */
if (iend == 5) ido = 3;
}
}
void fcn(int neq, int ido, float t, float y[], float hidrvs[])
{
hidrvs[0] = -9.8 - .005/y[2]*y[1];
hidrvs[1] = -1.e-8 * y[1] * y[1];
}
Output
T Y1/Y2 Y1P Y1PP/Y2PP
10.0000 89773.0391 -1044.0096 -3.9701
0.8954 -0.0109
20.0000 79150.9922 -1078.6333 -2.9083
0.7826 -0.0116
30.0000 68240.9531 -1101.0377 -1.5031
0.6635 -0.0121
40.0000 57184.9180 -1106.9633 0.4253
0.5413 -0.0123
50.0000 46178.1445 -1089.8291 3.1699
0.4201 -0.0119
Warning Errors
|
IMSL_ TOLERANCE_TOO_SMALL |
The requested error tolerance, # is too small. Using # instead. |
|
IMSL_ RESTART |
The stepsize has been reduced too rapidly The integrator is going to do a restart. |
Fatal Errors
|
IMSL_ADJUST_STEPSIZE1 |
The current step length = #, is less than the minimum steplength, “hmin” = #, at the conclusion of the starting phase of the integration. Decreasing “hmin” to a value less than or equal to # may help. |
|
IMSL_ADJUST_STEPSIZE2 |
The integrator needs to take a step smaller than # in order to maintain the requested local error. Decreasing “hmin” to a value less than or equal to # may help. |
|
IMSL_INCORRECT_TEND |
Either the new output point precedes the last one or it has the same value. “tend” = #. |
|
IMSL_ADJUST_ERROR_TOLERANCE |
The step length, H = #, is so small that when Tn + H is formed, the result will be the same as Tn, where Tn is the base value of the independent variable. If this problem is not due to a nonintegrable singularity, it can probably be corrected by translating “t” so that it is closer to 0. Reducing the error tolerance for the equations through argument “eqnerr” may also help with this problem. |
|
IMSL_ERROR_TOLERANCE |
A local error tolerance of zero has been requested. |
|
IMSL_ERROR_PREVIOUS |
A fatal error has occurred because of the error reported in the previous error message. |
|
|
|
