Solves a system of one-dimensional time-dependent partial differential equations using a moving-grid interface.
Synopsis
#include <imsl.h>
void imsl_f_pde_1d_mg_mgr (int task, void **state, …, 0)
void imsl_f_pde_1d_mg (int npdes, int ngrids, float *t, float tend float u[], float xl, float xr, void *state, void pde_systems(), void boundary_conditions(), …, 0)
The void functions imsl_d_pde_1d_mg_mgr and imsl_d_pde_1d_mg are for double type arithmetic accuracy.
The function imsl_f_pde_1d_mg_mgr is used to initialize and reset the problem, and the function imsl_f_pde_1d_mg is the integrator. The descriptions of both functions are provided below.
NOTE: The integrator is provided with single or double precision arithmetic. We recommend using the double precision interface imsl_d_pde_1d_mg.
Required Arguments for imsl_f_pde_1d_mg_mgr
int task
(Input)
This function must be called with task set to IMSL_PDE_INITIALIZE to
set up for solving a system and with task equal to IMSL_PDE_RESET to
clean up after it has been solved. These values for task are defined in
the include file, imsl.h.
void **state
(Input/Output)
The current state of the PDE solution is held in a structure
pointed to by state. It cannot
be directly manipulated.
Required Arguments for imsl_f_pde_1d_mg
int npdes
(Input)
The number of differential equations.
int ngrids
(Input)
The number of spatial grid/mesh points, including the boundary points
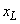and 
.
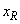float *t
(Input/Output)
On input, t is the initial
independent variable value. On output, t is replaced by tend, unless error
conditions arise. This is first set to the value of the independent variable
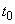where the integration of 
begins. It is set to the value tend on return.
float tend
(Input)
Mathematical value of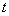 
where the integration
ofends. Note: Starting values of
t < tend imply integration
in the forward direction, while values of t > tend imply integration
in the backward direction. Either direction is permitted.
float u[]
(Input/Output)
Array of size npdes+1 by ngrids. On input, the
first npdes rows
contain initial values for all components of the system at the equally spaced
grid of values. It is not required to define the grid values in the last row of
u. On output
u[] contains the
approximate solution value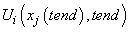 
at array location u[i*ngrids+j]. The grid value 
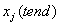is in location u[(npdes*ngrids) +j]. Normally
the grid values are equally spaced as the integration starts. Variable grid
values can be provided by defining them as output from the user function initial_conditions
supplied by either imsl_f_pde_1d_mg_mgr’s
IMSL_INITIAL_CONDITIONS,
or IMSL_INITIAL_CONDITIONS_W_DATA
optional arguments.
float xl
(Input)
Lower grid boundary, .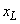
float xr
(Input)
Upper grid boundary, .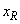
void *state
(Input/Output)
The current state of the solution is held in a structure
pointed to by state. It must be
initialized by a call to imsl_f_pde_1d_mg_mgr.
It cannot be directly manipulated.
void pde_systems(float t,
float x,
int npdes,
int ngrids,
float *full_u,
float *grid_u,
float *dudx,
float *c,
float *q,
float *r,
int *ires)
(Input)
A user-supplied function to evaluate the differential equation, as
expressed in Equation 2.
Each application requires a function specifically designed for the task, and
this function is normally written by the user of the integrator.
Evaluate the terms of the system of Equation 2. A
default value of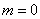 
is assumed, but this can be
changed to one of the choices,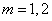 
. Use the optional arguments
IMSL_CART_COORDINATES,
IMSL_CYL_COORDINATES,
IMSL_SPH_COORDIANTES
for the respective values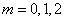 
. Return the values in the
arrays as indicated:
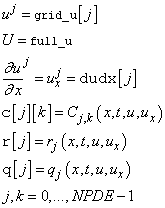
If any of the functions cannot be evaluated, set ires=3. Otherwise, do not change the value of ires.
void boundary_conditions
(float t,
float *beta,
float *gamma,
float *full_u,
float *grid_u,
float *dudx,
int npdes,
int grids,
int left,
int *ires)
(Input)
User-supplied function to supply the boundary conditions, as
expressed in Equation 2.
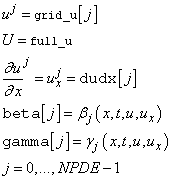
The value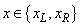 
, and the flag left=1 for 
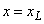. The flag has the value left=0 for 
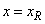. If any of the functions cannot be
evaluated, set ires=3. Otherwise, do not
change the value of ires.
Synopsis with Optional Arguments for imsl_f_pde_1d_mg_mgr
#include <imsl.h>
void imsl_f_pde_1d_mg_mgr (int task, void **state,
IMSL_CART_COORDINATES, or
IMSL_CYL_COORDINATES, or
IMSL_SPH_COORDINATES,
IMSL_TIME_SMOOTHING, float tau,
IMSL_SPATIAL_SMOOTHING, float kappa,
IMSL_MONITOR_REGULARIZING, float alpha,
IMSL_MAX_BDF_ORDER, int max_bdf_order,
IMSL_USER_FACTOR_SOLVE, int fac(), void sol(),
IMSL_USER_FACTOR_SOLVE_W_DATA, int fac(), void sol(), void data,
IMSL_INITIAL_CONDITIONS, void initial_conditions()
IMSL_INITIAL_CONDITIONS_W_DATA, void initial_conditions(), void data,
0)
Optional Arguments
IMSL_CART_COORDINATES, or
IMSL_CYL_COORDINATES, or
IMSL_SPH_COORDINATES
IMSL_CART_COORDINATES
specifies cartesian coordinates, where 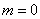in Equation 2. IMSL_CYL_COORDINATES
specifies cylindrical or polar coordinates, where 
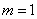in Equation 2. IMSL_SPH_COORDINATES
specifies spherical coordinates, where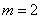 
in Equation 2.
Default:
IMSL_CART_COORDINATES
IMSL_TIME_SMOOTHING,
float tau,
(Input)
Resets the value of the parameter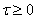 
, described above.
Default: 
.
IMSL_SPATIAL_SMOOTHING,
float kappa,
(Input)
Resets the value of the parameter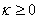 
, described above.
Default:
.
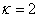IMSL_MONITOR_REGULARIZING,
float alpha,
(Input)
Resets the value of the parameter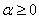 
, described above.
Default:
.
IMSL_MAX_BDF_ORDER,
int max_bdf_order,
(Input)
Resets the maximum order for the bdf formulas used in imsl_f_dea_petzold_gear.
The new value can be any integer between 1 and 5. Some problems benefit by
making this change. The default value of max_bdf_order was
chosen because imsl_f_dea_petzold_gear
may cycle on its selection of order and step-size with max_bdf_order higher
than value 2.
Default: max_bdf_order=2.
IMSL_USER_FACTOR_SOLVE,
int fac(int neq,
int iband,
float *a),
void sol(int neq,
int iband,
float *g,
float *y)
(Input)
User-supplied functions to factor A, and solve the system
A∆y = ∆g. Use of this
optional argument allows for handling the factorization and solution steps in a
problem-specific manner. If successful fac should return 0,
if unsuccessful, fac should return a
non-zero value. See Example 5-A Flame Propagation Model
for sample usage of this optional argument.
IMSL_USER_FACTOR_SOLVE_W_DATA,
int fac(int neq,
int iband,
float *a, void *data),
void sol(int neq,
int iband,
float *g, float
*y, void *data),
void *data
(Input)
User-supplied functions to factor A, and solve the system
A∆y = ∆g. The argument data is a pointer to
the data that is passed to the user-supplied function.
IMSL_INITIAL_CONDITIONS,
void initial_conditions(int npdes, int ngrids, float *u)
(Input)
User-supplied function to supply the initial values for the system at
the starting independent variable value t. This function can
also provide a non-uniform grid at the initial value. Here npdes is the number of
differential equations, ngrids is the number
of grid points, and u is an array of size
npdes+1 by ngrids, containing the
approximate solution value 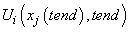in location u[i*ngrids+j]. The grid values are equally spaced
on input, but can be updated as desired, provided the values are
increasing. Update the grid values in array locations u[(npdes*ngrids) +j],
where 0 ≤ j < ngrids.
IMSL_INITIAL_CONDITIONS_W_DATA,
void initial_conditions(int npdes, int ngrids, float *u, float *grid,
void *data),
void *data
(Input)
User-supplied function to supply the initial values for the system at
the starting independent variable value t. This function can
also provide a non-uniform grid at the initial value. The argument data is a pointer to
the data that is passed to the user-supplied function.
Synopsis with Optional Arguments for imsl_f_pde_1d_mg
#include <imsl.h>
void imsl_f_pde_1d_mg (int npdes, int ngrids, float *t, float tend, float u[], float xl, float xr, void *state, void pde_systems(), void boundary_conditions(),
IMSL_RELATIVE_TOLERANCE, float rtol,
IMSL_ABSOLUTE_TOLERANCE, float atol,
IMSL_PDE_SYS_W_DATA, void pde_systems(), void *data,
IMSL_BOUNDARY_COND_W_DATA, void bounary_conditions(), void *data,
0)
Optional Arguments
IMSL_RELATIVE_TOLERANCE,
float rtol,
(Input)
This option resets the value of the relative accuracy parameter used
in imsl_f_dea_petzold_gear.
Default: rtol=1.0E-2 for single
precision, rtol=1.0E-4 for double
precision.
IMSL_ABSOLUTE_TOLERANCE,
float atol,
(Input)
This option resets the value of the absolute accuracy parameter used
in imsl_f_dea_petzold_gear.
Default:
atol=1E-2 for
single precision, atol=1E-4 for double
precision.
IMSL_PDE_SYS_W_DATA, void pde_systems(float t,
float x,
int npdes,
int ngrids,
float *full_u,
float *grid_u,
float *dudx,
float *c,
float *q,
float *r,
int *ires,
void *data),
void *data
(Input)
User-supplied function to evaluate the differential equation, as
expressed in Equation 2.
The argument data is a pointer to
the data that is passed to the user-supplied function.
IMSL_BOUNDARY_COND_W_DATA, void boundary_conditions
(float t,
float *beta,
float *gamma,
float *full_u,
float *grid_u,
float *dudx,
int npdes,
int ngrids,
int left,
int *ires, void *data),
void *data
(Input)
User-supplied function to supply the boundary conditions, as
expressed in Equation 2.
The argument data is a pointer to
the data that is passed to the user-supplied function.
Examples
Remarks on the Examples
Due to its importance and the complexity of its interface, function imsl_f_pde_1d_mg is presented with several examples. Many of the program features are exercised. The problems complete without any change to the optional arguments, except where these changes are required to describe or to solve the problem.
In many applications the solution to a PDE is used as an auxiliary variable, perhaps as part of a larger design or simulation process. The truncation error of the approximate solution is commensurate with piece-wise linear interpolation on the grid of values, at each output point. To show that the solution is reasonable, a graphical display is revealing and helpful. We have not provided graphical output as part of our documentation, but users may already have the Rogue Wave, Inc. product, PV-WAVE, which is not included with IMSL C Numerical Library. Examples 1-8 write results in files pde_ex0#.out that can be visualized with PV-WAVE. We provide a script of commands, pde_1d_mg_plot.pro, for viewing the solutions. This is listed below. The grid of values and each consecutive solution component is displayed in separate plotting windows. The script and data files written by examples 1-8 on a SUN-SPARC system are in the directory for IMSL C Numerical Library examples. When executing PV_WAVE, use the command line
pde_1d_mg_plot,filename=’pde_ex0#.out’
to view the output of a particular example. The symbol ‘#’ will be one of the choices 1,2,…,8. However, it is not necessary to have PV_WAVE installed to execute the examples.
To view the code, see Code for PV-WAVE Plotting.
Example 1 - Electrodynamics Model
This example is from Blom and Zegeling (1994). The system is
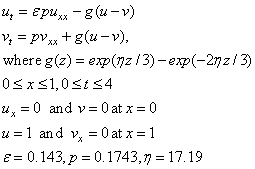
We make the connection between the model problem statement and the example:
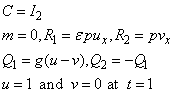
The boundary conditions are
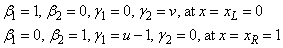
This is a non-linear problem with
sharply changing conditions near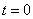 
. The default settings
of integration parameters allow the problem to be solved. The use of
imsl_f_pde_1d_mg
requires two subroutines provided by the user to describe the differential
equations, and boundary conditions.
#include <stdio.h>
#include <math.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double u[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[], double *c,
double q[], double r[], int *ires);
static void boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[], int npdes,
int ngrids, int left, int *ires);
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 2
#define NFRAMES 5
#define N 51
#define U(I_,J_) u[I_ * ngrids + J_]
int main ()
{
char *state = NULL;
int i, j;
double u[(NPDE + 1) * N];
double t0 = 0.0, tout;
double delta_t = 10.0, tend = 4.0;
int npdes = NPDE, ngrids = N;
double xl = 0.0, xr = 1.0;
FILE *file1;
file1 = fopen ("pde_ex01.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
fprintf (file1, " %d\t%d\t%d", npdes, ngrids, NFRAMES);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, t0, tend);
/* initialize u */
initial_conditions (npdes, ngrids, u);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state, 0);
tout = 1e-3;
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &t0, tout, u, xl, xr, state,
pde_systems, boundary_conditions, 0);
fprintf (file1, "%f\n", tout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
t0 = tout;
tout = tout * delta_t;
tout = MIN (tout, tend);
}
while (t0 < tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
#undef MIN
#undef NPDE
#undef NFRAMES
#undef N
#undef U
}
static void
initial_conditions (int npdes, int ngrids, double u[])
{
#define U(I_,J_) u[I_ * ngrids + J_]
int i;
for (i = 0; i < ngrids; i++)
{
U (0, i) = 1.0;
U (1, i) = 0.0;
}
#undef U
}
static void
pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[], double *c,
double q[], double r[], int *ires)
{
#define C(I_,J_) c[I_ * npdes + J_]
double z;
static double eps = 0.143;
static double eta = 17.19;
static double pp = 0.1743;
C (0, 0) = 1.0;
C (0, 1) = 0.0;
C (1, 0) = 0.0;
C (1, 1) = 1.0;
r[0] = pp * dudx[0] * eps;
r[1] = pp * dudx[1];
z = eta * (grid_u[0] - grid_u[1]) / 3.0;
q[0] = exp (z) - exp (-2.0 * z);
q[1] = -q[0];
return;
#undef C
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[],
int ngrids, int npdes, int left, int *ires)
{
if (left)
{
beta[0] = 1.0;
beta[1] = 0.0;
gamma[0] = 0.0;
gamma[1] = grid_u[1];
}
else
{
beta[0] = 0.0;
beta[1] = 1.0;
gamma[0] = grid_u[0] - 1.0;
gamma[1] = 0.0;
}
return;
}
Example 2 - Inviscid Flow on a Plate
This example is a first order system from Pennington and Berzins, (1994). The equations are
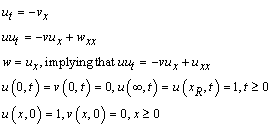
Following elimination of w, there remain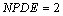
differential equations. The
variable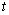 
is not time, but a second space
variable. The integration goes from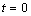 
to 
. It is necessary to truncate
the variable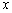 
at a finite value, say 
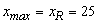. In terms of the integrator,
the system is defined by letting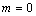 
and
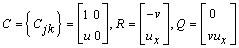
The boundary conditions are satisfied by
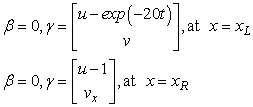
We use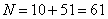 
grid points and output
the solution at steps of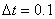 
.
This is a non-linear boundary layer problem with sharply
changing condition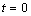s near . The problem statement
was modified so that boundary conditions are continuous near 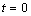. Without this change the
underlying integration software, imsl_f_dea_petzold_gear,
cannot solve the problem. The continuous blending function 
is arbitrary and artfully
chosen. This is a mathematical change to the problem, required because of
the stated discontinuity at 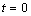. Reverse communication
is used for the problem data. No additional user-written subroutines are
required when using reverse communication. We also have chosen 10 of the
initial grid points to be concentrated near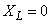 
, anticipating rapid change in the
solution near that point. Optional changes are made to use a pure absolute
error tolerance and non-zero time-smoothing.
#include <stdio.h>
#include <math.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double u[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[],
double dudx[], double *c, double q[],
double r[], int *ires);
static void boundary_conditions (double t, double beta[],
double gamma[], double full_u[],
double grid_u[], double dudx[],
int npdes, int ngrids, int left,
int *ires);
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 2
#define N1 10
#define N2 51
#define N (N1+N2)
#define U(I_,J_) u[I_ * ngrids + J_]
FILE *file1;
int main ()
{
char *state;
int i, j;
int nframes;
double u[(NPDE + 1) * N];
double t0 = 0.0, tout;
double delta_t = 1e-1, tend = 5.0;
int npdes = NPDE, ngrids = N;
double xl = 0.0, xr = 25.0;
double tau = 1.0e-3;
double atol = 1e-2;
double rtol = 0.0;
file1 = fopen ("pde_ex02.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
nframes = (int) ((tend + delta_t) / delta_t);
fprintf (file1, " %d\t%d\t%d", npdes, ngrids, nframes);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, t0, tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state,
IMSL_TIME_SMOOTHING, tau,
IMSL_INITIAL_CONDITIONS, initial_conditions, 0);
t0 = 0.0;
tout = delta_t;
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &t0, tout, u, xl,
xr, state, pde_systems, boundary_conditions,
IMSL_RELATIVE_TOLERANCE, rtol,
IMSL_ABSOLUTE_TOLERANCE, atol, 0);
t0 = tout;
fprintf (file1, "%f\n", tout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
tout = tout + delta_t;
tout = MIN (tout, tend);
}
while (t0 < tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
fclose (file1);
#undef MIN
#undef NPDE
#undef NFRAMES
#undef N
#undef U
}
static void
initial_conditions (int npdes, int ngrids, double u[])
{
#define U(I_,J_) u[I_* ngrids + J_]
int i, j, i_, n1 = 10, n2 = 51, n;
double dx1, dx2;
double xl = 0.0, xr = 25.0;
n = n1 + n2;
for (i = 0; i < ngrids; i++)
{
U (0, i) = 1.0;
U (1, i) = 0.0;
U (2, i) = 0.0;
}
dx1 = xr / n2;
dx2 = dx1 / n1;
/* grid */
for (i = 1; i <= n1; i++)
{
i_ = i - 1;
U (2, i_) = (i - 1) * dx2;
}
for (i = n1 + 1; i <= n; i++)
{
i_ = i - 1;
U (2, i_) = (i - n1) * dx1;
}
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
#undef U
}
static void
pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[],
double *c, double q[], double r[], int *ires)
{
#define C(I_,J_) c[I_ * npdes + J_]
double z;
C (0, 0) = 1.0;
C (1, 0) = 0.0;
C (0, 1) = grid_u[0];
C (1, 1) = 0.0;
r[0] = -grid_u[1];
r[1] = dudx[0];
q[0] = 0.0;
q[1] = grid_u[1] * dudx[0];
return;
#undef C
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires)
{
double dif;
beta[0] = 0.0;
beta[1] = 0.0;
if (left)
{
dif = exp (-20.0 * t);
gamma[0] = grid_u[0] - dif;
gamma[1] = grid_u[1];
}
else
{
gamma[0] = grid_u[0] - 1.0;
gamma[1] = dudx[1];
}
return;
}
Example 3 - Population Dynamics
This example is from Pennington and Berzins (1994). The system is
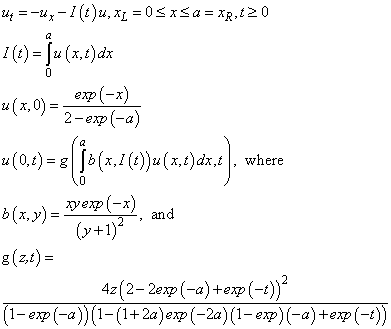
This is a notable problem because it involves the unknown
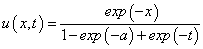
across the entire domain. The software can solve the problem by introducing two dependent algebraic equations:
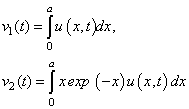
This leads to the modified system
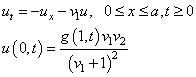
In the interface to the evaluation of the differential
equation and boundary conditions, it is necessary to evaluate the integrals,
which are computed with the values of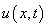 
on the grid. The integrals are
approximated using the trapezoid rule, commensurate with the truncation error in
the integrator.
This is a non-linear integro-differential problem involving
non-local conditions for the differential equation and boundary
conditions. Access to evaluation of these conditions is provided using the
optional arguments IMSL_PDE_SYS_W_DATA
and IMSL_BOUNDARY_COND_W_DATA.
Optional changes are made to use an absolute error tolerance and non-zero
time-smoothing. The time-smoothing value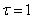 
prevents grid lines from crossing.
#include <stdio.h>
#include <math.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double u[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[],
double dudx[], double *c, double q[],
double r[], int *ires);
static void boundary_conditions (double t, double beta[],
double gamma[], double full_u[],
double grid_u[], double dudx[],
int npdes, int ngrids, int left,
int *ires);
static double fcn_g (double z, double t);
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 1
#define N 101
#define U(I_,J_) u[I_ * ngrids + J_]
FILE *file1;
int main ()
{
int i, j, nframes;
double u[(NPDE + 1) * N], mid[N - 1];
int npdes = NPDE, ngrids = N;
double t0 = 0.0, tout;
double delta_t = 1e-1, tend = 5.0, a = 5.0;
char *state;
double xl = 0.0, xr = 5.0;
double *ptr_u;
double tau = 1.0;
double atol = 1e-2;
double rtol = 0.0;
file1 = fopen ("pde_ex03.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
nframes = (int) (tend + delta_t) / delta_t;
fprintf (file1, " %d\t%d\t%d", npdes, ngrids, nframes);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, t0, tend);
ptr_u = u;
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state,
IMSL_TIME_SMOOTHING, tau,
IMSL_INITIAL_CONDITIONS, initial_conditions, 0);
tout = delta_t;
fprintf (file1, "%f\n", t0);
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &t0, tout, u, xl,
xr, state, pde_systems, boundary_conditions,
IMSL_RELATIVE_TOLERANCE, rtol,
IMSL_ABSOLUTE_TOLERANCE, atol, 0);
t0 = tout;
if (t0 <= tend)
{
fprintf (file1, "%f\n", tout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
}
tout = MIN (tout + delta_t, tend);
}
while (t0 < tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
fclose (file1);
#undef MIN
#undef NPDE
#undef N
#undef XL
#undef XR
#undef U
}
static void
initial_conditions (int npdes, int ngrids, double u[])
{
#define U(I_,J_) u[I_ * ngrids + J_]
#define XL 0.0
#define XR 5.0
int i, j;
double dx, xi;
dx = (XR - XL) / (ngrids - 1);
for (i = 0; i < ngrids; i++)
{
U (0, i) = exp (-U (1, i)) / (2.0 - exp (-XR));
}
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
#undef U
#undef XL
#undef XR
}
static void
pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[],
double *c, double q[], double r[], int *ires)
{
#define U(I_,J_) full_u[I_ * ngrids + J_]
double v1;
double sum = 0.0;
int i;
c[0] = 1.0;
r[0] = -1 * grid_u[0];
for (i = 0; i < ngrids - 1; i++)
{
sum += (U (0, i) + U (0, i + 1)) * (U (1, i + 1) - U (1, i));
}
v1 = 0.5 * sum;
q[0] = v1 * grid_u[0];
return;
#undef U
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires)
{
#define U(I_,J_) full_u[I_ * ngrids + J_]
double v1, v2, mid;
double sum = 0.0;
double sum1 = 0.0, sum2 = 0.0, sum3 = 0.0, sum4 = 0.0;
int i;
for (i = 0; i < ngrids - 1; i++)
{
sum += (U (0, i) + U (0, i + 1)) * (U (1, i + 1) - U (1, i));
mid = 0.5 * (U (1, i) + U (1, i + 1));
sum1 += mid * exp (-mid) *
((U (0, i) + U (0, i + 1)) * (U (1, i + 1) - U (1, i)));
}
if (left)
{
v1 = 0.5 * sum;
v2 = 0.5 * sum1;
beta[0] = 0.0;
gamma[0] = fcn_g (1.0, t) * v1 * v2 /
((v1 + 1.0) * (v1 + 1.0)) - grid_u[0];
}
else
{
beta[0] = 0.0;
gamma[0] = dudx[0];
}
return;
#undef U
}
static double
fcn_g (double z, double t)
{
double g, a = 5.0;
g = 4.0 * z * (2.0 - 2.0 * exp (-a) + exp (-t)) *
(2.0 - 2.0 * exp (-a) + exp (-t));
g = g / ((1.0 - exp (-a)) * (1.0 - (1.0 + 2.0 * a) *
exp (-2.0 * a)) * (1.0 - exp (-a) + exp (-t)));
return g;
}
Example 4 - A Model in Cylindrical Coordinates
This example is from Blom and Zegeling (1994). The system models a reactor-diffusion problem:
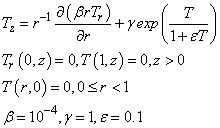
The axial direction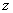 
is treated as a time
coordinate. The radius 
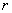is treated as the
single space variable.
This is a
non-linear problem in cylindrical coordinates. Our example illustrates assigning
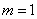in Equation 2. We provide the optional
argument IMSL_CYL_COORDINATES
that resets this value from its default, .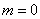
#include <stdio.h>
#include <math.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double t[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double u[], double grid_u[], double dudx[], double *c,
double q[], double r[], int *ires);
static void boundary_conditions (double t, double beta[],
double gamma[], double u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires);
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 1
#define N 41
#define T(I_,J_) t[I_ * ngrids + J_]
int main ()
{
int i, j, ido;
int nframes;
double t[(NPDE + 1) * N];
double z0 = 0.0, zout;
double dx1, dx2, diff;
double delta_z = 1e-1, zend = 1.0, zmax = 1.0;
double beta = 1e-4, gamma = 1.0, eps = 1e-1;
char *state;
int npdes = NPDE, ngrids = N;
double xl = 0.0, xr = 1.0;
FILE *file1;
int m = 1;
file1 = fopen ("pde_ex04.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
nframes = (int) ((zend + delta_z) / delta_z) - 1;
fprintf (file1, " %d\t%d\t%d", npdes, N, nframes);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, z0, zend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state, IMSL_CYL_COORDINATES, 0);
initial_conditions (npdes, ngrids, t);
zout = delta_z;
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &z0, zout, t, xl,
xr, state, pde_systems, boundary_conditions, 0);
z0 = zout;
if (z0 <= zend)
{
fprintf (file1, "%f\n", zout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", T (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
}
zout = MIN ((zout + delta_z), zend);
}
while (z0 < zend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
fclose (file1);
#undef MIN
#undef NPDE
#undef N
#undef T
}
static void
initial_conditions (int npdes, int ngrids, double t[])
{
#define T(I_,J_) t[I_ * ngrids + J_]
int i;
for (i = 0; i < ngrids; i++)
{
T (0, i) = 0.0;
}
#undef T
}
static void
pde_systems (double t, double x, int npdes, int ngrids, double u[],
double grid_u[], double dudx[], double *c,
double q[], double r[], int *ires)
{
#define C(I_,J_) c[I_ * npdes + J_]
static double beta = 01e-4, gamma = 1.0, eps = 1e-1;
C (0, 0) = 1.0;
r[0] = beta * dudx[0];
q[0] = -1.0 * gamma * exp (grid_u[0] / (1.0 + eps * grid_u[0]));
return;
#undef C
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires)
{
if (left)
{
beta[0] = 1.0;
gamma[0] = 0.0;
}
else
{
beta[0] = 0.0;
gamma[0] = grid_u[0];
}
return;
}
Example 5 - A Flame Propagation Model
This example is presented more fully in Verwer, et
al., (1989). The system is a normalized problem relating mass
density 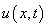and temperature 
:
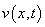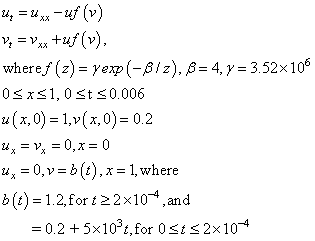
This is a non-linear problem. The example shows the model steps for replacing the banded solver in the software with one of the user’s choice. Following the computation of the matrix factorization in imsl_lin_sol_gen_band (see Chapter 1, Linear Systems), we declare the system to be singular when the reciprocal of the condition number is smaller than the working precision. This choice is not suitable for all problems. Attention must be given to detecting a singularity when this option is used.
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <math.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double u[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double u[], double grid_u[], double dudx[],
double *c, double q[], double r[], int *ires);
static void boundary_conditions (double t, double beta[],
double gamma[], double u[],
double grid_u[], double dudx[],
int npdes, int ngrids, int left,
int *ires);
static int fac (int neq, int iband, double *a);
static void sol (int neq, int iband, double *g, double *y);
static double fcn (double z);
int *ipvt = NULL;
double *factor = NULL;
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 2
#define N 40
#define NEQ ((NPDE+1)*N)
#define U(I_,J_) u[I_ * ngrids + J_]
int main ()
{
int i, j, nframes;
double u[(NPDE + 1) * N];
double t0 = 0.0, tout;
double delta_t = 1e-4, tend = 6e-3;
char *state;
int npdes = NPDE, ngrids = N;
double xl = 0.0, xr = 1.0;
FILE *file1;
double work[NEQ], rcond;
double xmax = 1.0, beta = 4.0, gamma = 3.52e6;
int max_bdf_order = 5;
file1 = fopen ("pde_ex05.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
nframes = (int) ((tend + delta_t) / delta_t) - 1;
fprintf (file1, " %d\t%d\t%d", npdes, ngrids, nframes);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, t0, tend);
initial_conditions (npdes, ngrids, u);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state,
IMSL_MAX_BDF_ORDER, max_bdf_order,
IMSL_USER_FACTOR_SOLVE, fac, sol, 0);
tout = delta_t;
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &t0, tout, u, xl,
xr, state, pde_systems, boundary_conditions, 0);
t0 = tout;
if (t0 <= tend)
{
fprintf (file1, "%f\n", tout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
}
}
tout = MIN ((tout + delta_t), tend);
}
while (t0 < tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
fclose (file1);
if (factor != NULL)
{
imsl_free (factor);
}
if (ipvt != NULL)
{
imsl_free (ipvt);
}
}
#undef MIN
#undef U
static void
initial_conditions (int npdes, int ngrids, double u[])
{
#define U(I_,J_) u[I_ * ngrids + J_]
int i;
for (i = 0; i < ngrids; i++)
{
U (0, i) = 1.0;
U (1, i) = 2e-1;
}
#undef U
}
static void
pde_systems (double t, double x, int npdes, int ngrids, double u[],
double grid_u[], double dudx[], double *c,
double q[], double r[], int *ires)
{
#define C(I_,J_) c[I_ * npdes + J_]
C (0, 0) = 1.0;
C (0, 1) = 0.0;
C (1, 0) = 0.0;
C (1, 1) = 1.0;
r[0] = dudx[0];
r[1] = dudx[1];
q[0] = grid_u[0] * fcn (grid_u[1]);
q[1] = -1.0 * q[0];
return;
#undef C
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires)
{
if (left)
{
beta[0] = 0.0;
beta[1] = 0.0;
gamma[0] = dudx[0];
gamma[1] = dudx[1];
}
else
{
beta[0] = 1.0;
gamma[0] = 0.0;
beta[1] = 0.0;
if (t >= 2e-4)
{
gamma[1] = 12e-1;
}
else
{
gamma[1] = 2e-1 + 5e3 * t;
}
gamma[1] -= grid_u[1];
}
return;
}
/* Factor the banded matrix. This is the same solver used
* internally but that is not required. A user can substitute
* one of their own.
* Note: Allowing lin_sol_gen_band to allocate ipvt and factor
* variables, then use in sol function.
*/
static int
fac (int neq, int iband, double *a)
{
double rcond, panic_flag;
int i, j;
double b[NEQ];
/* Free factor and pivot sequence if previously allocated. */
if (factor != NULL)
{
imsl_free (factor);
factor = NULL;
}
if (ipvt != NULL)
{
imsl_free (ipvt);
ipvt = NULL;
}
imsl_d_lin_sol_gen_band (neq, a, iband, iband, b,
IMSL_FACTOR, &ipvt, &factor,
IMSL_FACTOR_ONLY, IMSL_CONDITION, &rcond, 0);
panic_flag = 0;
if (1.0 / rcond <= imsl_d_machine (4))
panic_flag = 3;
return panic_flag;
}
static void
sol (int neq, int iband, double *g, double *y)
{
imsl_d_lin_sol_gen_band (neq, (double *) NULL, iband, iband, g,
IMSL_SOLVE_ONLY,
IMSL_FACTOR_USER, ipvt, factor,
IMSL_RETURN_USER, y, 0);
return;
}
static double
fcn (double z)
{
double beta = 4.0, gamma = 3.52e6;
return gamma * exp (-1.0 * beta / z);
}
Example 6 - A ‘Hot Spot’ Model
This example is presented more fully in Verwer, et
al., (1989). The system is a normalized problem relating the
temperature 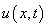, of a reactant in a chemical
system. The formula for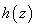 
is equivalent to their
example.
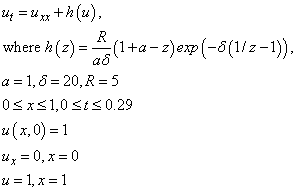
#include <stdio.h>
#include <math.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double u[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[],
double dudx[], double *c, double q[],
double r[], int *ires);
static void boundary_conditions (double t, double beta[],
double gamma[], double full_u[],
double grid_u[], double dudx[],
int npdes, int ngrids, int left,
int *ires);
static double fcn_h (double z);
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 1
#define N 80
#define U(I_,J_) u[I_ * ngrids + J_]
int main ()
{
int i, j, nframes;
double u[(NPDE + 1) * N];
double t0 = 0.0, tout;
double delta_t = 1e-2, tend = 29e-2;
double u0 = 1.0, u1 = 0.0, tdelta = 1e-1, tol = 29e-2;
double a = 1.0, delta = 20.0, r = 5.0;
char *state;
int npdes = NPDE, ngrids = N;
double xl = 0.0, xr = 1.0;
FILE *file1;
int max_bdf_order = 5;
file1 = fopen ("pde_ex06.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
nframes = (int) ((tend + delta_t) / delta_t) - 1;
fprintf (file1, " %d\t%d\t%d", npdes, ngrids, nframes);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, t0, tend);
initial_conditions (npdes, ngrids, u);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state,
IMSL_MAX_BDF_ORDER, max_bdf_order, 0);
tout = delta_t;
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &t0, tout, u, xl,
xr, state, pde_systems, boundary_conditions, 0);
t0 = tout;
if (t0 <= tend)
{
fprintf (file1, "%f\n", tout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0) fprintf (file1, "\n");
}
}
}
tout = MIN ((tout + delta_t), tend);
}
while (t0 < tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
fclose (file1);
#undef MIN
#undef NPDE
#undef N
#undef U
}
static void
initial_conditions (int npdes, int ngrids, double u[])
{
#define U(I_,J_) u[I_ * ngrids + J_]
int i;
for (i = 0; i < ngrids; i++)
{
U (0, i) = 1.0;
}
#undef U
}
static void
pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[],
double *c, double q[], double r[], int *ires)
{
#define C(I_,J_) c[I_ * npdes + J_]
c[0] = 1.0;
r[0] = dudx[0];
q[0] = -fcn_h (grid_u[0]);
return;
#undef C
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires)
{
if (left)
{
beta[0] = 0.0;
gamma[0] = dudx[0];
}
else
{
beta[0] = 0.0;
gamma[0] = grid_u[0] - 1.0;
}
return;
}
static double
fcn_h (double z)
{
double a = 1.0, delta = 2e1, r = 5.0;
return (r / (a * delta)) * (1.0 + a - z) *
exp (-delta * (1.0 / z - 1.0));
}
Example 7 - Traveling Waves
This example is presented more fully in Verwer, et
al., (1989). The system is a normalized problem relating the
interaction of two waves, 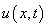and 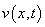moving in opposite
directions. The waves meet and reduce in amplitude, due to the non-linear
terms in the equation. Then they separate and travel onward, with reduced
amplitude.
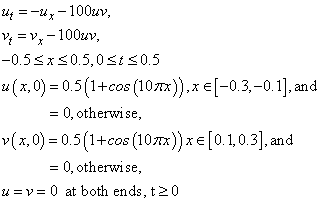
This is a non-linear system of first order equations.
#include <stdio.h>
#include <math.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double u[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[],
double dudx[], double *c, double q[],
double r[], int *ires);
static void boundary_conditions (double t, double beta[],
double gamma[], double full_u[],
double grid_u[], double dudx[],
int npdes, int ngrids, int left,
int *ires);
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 2
#define N 50
#define XL (-0.5)
#define XR 0.5
#define U(I_,J_) u[I_ * ngrids + J_]
FILE *file1;
int main ()
{
int i, j, nframes;
double u[(NPDE + 1) * N];
double t0 = 0.0, tout;
double delta_t = 5e-2, tend = 5e-1;
char *state;
int npdes = NPDE, ngrids = N;
double xl = XL, xr = XR;
double tau = 1e-3;
double atol = 1e-3;
double rtol = 0.0;
int max_bdf_order = 3;
file1 = fopen ("pde_ex07.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
nframes = (int) ((tend + delta_t) / delta_t);
fprintf (file1, " %d\t%d\t%d", npdes, ngrids, nframes);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, t0, tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state,
IMSL_TIME_SMOOTHING, tau,
IMSL_MAX_BDF_ORDER, max_bdf_order,
IMSL_INITIAL_CONDITIONS, initial_conditions, 0);
fprintf (file1, "%f\n", t0);
tout = delta_t;
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &t0, tout, u, xl,
xr, state, pde_systems, boundary_conditions,
IMSL_RELATIVE_TOLERANCE, rtol,
IMSL_ABSOLUTE_TOLERANCE, atol, 0);
t0 = tout;
if (t0 <= tend)
{
fprintf (file1, "%f\n", tout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
}
tout = MIN ((tout + delta_t), tend);
}
while (t0 < tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
fclose (file1);
#undef MIN
#undef NPDE
#undef N
#undef XL
#undef XR
#undef U
}
static void
initial_conditions (int npdes, int ngrids, double u[])
{
#define U(I_,J_) u[I_ * ngrids + J_]
#define XL -0.5
#define XR 0.5
int i, j;
double _pi, pulse;
double dx, xi;
_pi = imsl_d_constant("pi",0);
for (i = 0; i < ngrids; i++)
{
pulse = (0.5 * (1.0 + cos (10.0 * _pi * U (npdes, i))));
U (0, i) = pulse;
U (1, i) = pulse;
}
for (i = 0; i < ngrids; i++)
{
if ((U (npdes, i) < -3e-1) || (U (npdes, i) > -1e-1))
{
U (0, i) = 0.0;
}
if ((U (npdes, i) < 1e-1 || U (npdes, i) > 3e-1))
{
U (1, i) = 0.0;
}
}
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
fprintf (file1, "\n");
}
#undef XL
#undef XR
#undef U
}
static void
pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[],
double *c, double q[], double r[], int *ires)
{
#define C(I_,J_) c[I_ * npdes + J_]
C (0, 0) = 1.0;
C (0, 1) = 0.0;
C (1, 0) = 0.0;
C (1, 1) = 1.0;
r[0] = -1.0 * grid_u[0];
r[1] = grid_u[1];
q[0] = 100.0 * grid_u[0] * grid_u[1];
q[1] = q[0];
return;
#undef C
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires)
{
beta[0] = 0.0;
beta[1] = 0.0;
gamma[0] = grid_u[0];
gamma[1] = grid_u[1];
return;
}
Example 8 - Black-Scholes
The value of a European “call option,”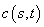 
, with exercise price 
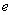and expiration date 
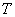, satisfies the “asset-or-nothing
payoff ”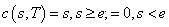 
. Prior to expiration 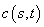is estimated by the
Black-Scholes differential equation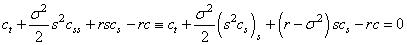 
. The parameters in the model
are the risk-free interest rate, 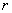, and the stock
volatility,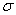
. The boundary conditions are
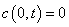and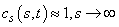 
. This development is described
in Wilmott, et al. (1995), pages 41-57. There are explicit
solutions for this equation based on the Normal Curve of Probability. The
normal curve, and the solution itself, can be efficiently computed with the IMSL
function imsl_f_normal_cdf, see Chapter 9, “Special Functions.”
With numerical integration the equation itself or the payoff can be readily
changed to include other formulas,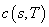 
, and corresponding boundary
conditions. We use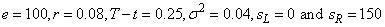 
.
This is a linear problem but with initial conditions that
are discontinuous. It is necessary to use a positive time-smoothing value
to prevent grid lines from crossing. We have used an absolute tolerance of
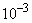. In $US, this is one-tenth of a
cent.
#include <stdio.h>
#include <imsl.h>
/* prototypes */
static void initial_conditions (int npdes, int ngrids, double u[]);
static void pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[], double *c,
double q[], double r[], int *ires);
static void boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[], int npdes,
int ngrids, int left, int *ires);
#define MIN(X,Y) (X<Y)?X:Y
#define NPDE 1
#define N 100
#define XL 0.0
#define XR 150.0
#define U(I_,J_) u[I_ * ngrids + J_]
int main ()
{
int i, j, nframes;
double u[(NPDE + 1) * N];
double t0 = 0.0, tout, xval;
double delta_t = 25e-3, tend = 25e-2;
double xmax = 150.0;
char *state;
int npdes = NPDE, ngrids = N;
double xl = XL, xr = XR;
FILE *file1;
double tau = 5e-3;
double atol = 1e-2;
double rtol = 0.0;
int max_bdf_order = 5;
file1 = fopen ("pde_ex08.out", "w");
imsl_output_file (IMSL_SET_OUTPUT_FILE, file1, 0);
nframes = (int) ((tend + delta_t) / delta_t);
fprintf (file1, " %d\t%d\t%d", npdes, ngrids, nframes);
fprintf (file1, "\t%f\t%f\t%f\t%f\n", xl, xr, t0, tend);
initial_conditions (npdes, ngrids, u);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_INITIALIZE, &state,
IMSL_TIME_SMOOTHING, tau,
IMSL_MAX_BDF_ORDER, max_bdf_order, 0);
tout = delta_t;
do
{
imsl_d_pde_1d_mg (npdes, ngrids, &t0, tout, u, xl,
xr, state, pde_systems, boundary_conditions,
IMSL_RELATIVE_TOLERANCE, rtol,
IMSL_ABSOLUTE_TOLERANCE, atol, 0);
t0 = tout;
if (t0 <= tend)
{
fprintf (file1, "%f\n", tout);
for (i = 0; i < npdes + 1; i++)
{
for (j = 0; j < ngrids; j++)
{
fprintf (file1, "%16.10f ", U (i, j));
if (((j + 1) % 4) == 0)
fprintf (file1, "\n");
}
}
}
tout = MIN ((tout + delta_t), tend);
}
while (t0 < tend);
imsl_d_pde_1d_mg_mgr (IMSL_PDE_RESET, &state, 0);
fclose (file1);
#undef MIN
#undef NPDE
#undef N
#undef XL
#undef XR
#undef U
}
static void
initial_conditions (int npdes, int ngrids, double u[])
{
#define U(I_,J_) u[I_ * ngrids + J_]
#define XL 0.0
#define XR 150.0
int i;
double dx, xi, xval, e = 100.0;
dx = (XR - XL) / (ngrids - 1);
for (i = 0; i < ngrids; i++)
{
xi = XL + i * dx;
if (xi <= e)
{
U (0, i) = 0.0;
}
else
{
U (0, i) = xi;
}
}
#undef U
#undef XL
#undef XR
}
static void
pde_systems (double t, double x, int npdes, int ngrids,
double full_u[], double grid_u[], double dudx[], double *c,
double q[], double r[], int *ires)
{
double sigsq, sigma = 2e-1, rr = 8e-2;
sigsq = sigma * sigma;
c[0] = 1.0;
r[0] = dudx[0] * x * x * sigsq * 0.5;
q[0] = -(rr - sigsq) * x * dudx[0] + rr * grid_u[0];
return;
}
static void
boundary_conditions (double t, double beta[], double gamma[],
double full_u[], double grid_u[], double dudx[],
int npdes, int ngrids, int left, int *ires)
{
if (left)
{
beta[0] = 0.0;
gamma[0] = grid_u[0];
}
else
{
beta[0] = 0.0;
gamma[0] = dudx[0] - 1.0;
}
return;
}
Code for PV-WAVE Plotting
PRO PDE_1d_mg_plot, FILENAME = filename, PAUSE = pause
;
if keyword_set(FILENAME) then file = filename else file = "res.dat"
if keyword_set(PAUSE) then twait = pause else twait = .1
;
; Define floating point variables that will be read
; from the first line of the data file.
xl = 0D0
xr = 0D0
t0 = 0D0
tlast = 0D0
;
; Open the data file and read in the problem parameters.
openr, lun, filename, /get_lun
readf, lun, npde, np, nt, xl, xr, t0, tlast
; Define the arrays for the solutions and grid.
u = dblarr(nt, npde, np)
g = dblarr(nt, np)
times = dblarr(nt)
;
; Define a temporary array for reading in the data.
tmp = dblarr(np)
t_tmp = 0D0
;
; Read in the data.
for i = 0, nt-1 do begin ; For each step in time
readf, lun, t_tmp
times(i) = t_tmp
for k = 0, npde-1 do begin ; For each PDE:
rmf, lun, tmp
u(i,k,*) = tmp ; Read in the components.
end
rmf, lun, tmp
g(i,*) = tmp ; Read in the grid.
end
;
; Close the data file and free the unit.
close, lun
free_lun, lun
;
; We now have all of the solutions and grids.
;
; Delete any window that is currently open.
while (!d.window NE -1) do WDELETE
;
; Open two windows for plotting the solutions
; and grid.
window, 0, xsize = 550, ysize = 420
window, 1, xsize = 550, ysize = 420
;
; Plot the grid.
wset, 0
plot, [xl, xr], [t0, tlast], /nodata, ystyle = 1, $
title = "Grid Points", xtitle = "X", ytitle = "Time"
for i = 0, np-1 do begin
oplot, g(*, i), times, psym = -1
end
;
; Plot the solution(s):
wset, 1
for k = 0, npde-1 do begin
umin = min(u(*,k,*))
umax = max(u(*,k,*))
for i = 0, nt-1 do begin
title = strcompress("U_"+string(k+1), /remove_all)+ $
" at time "+string(times(i))
plot, g(i, *), u(i,k,*), ystyle = 1, $
title = title, xtitle = "X", $
ytitle = strcompress("U_"+string(k+1), /remove_all), $
xr = [xl, xr], yr = [umin, umax], $
psym = -4
wait, twait
end
end
end
