Performs multidimensional interpolation and differentiation for up to 7 dimensions.
Synopsis
float imsl_f_spline_nd_interp (int n, int d[], float x[], float xdata[], float fdata[], ..., 0)
The type double function is imsl_d_spline_nd_interp.
Required Arguments
int n
(Input)
The dimension of the problem. n cannot be greater
than seven.
int d[]
(Input)
Array of length n. d[i] contains the number
of gridpoints in the i-th direction.
float x[]
(Input)
Array of length n containing the point
at which interpolation is to be done.
An interpolant is to be calculated at
the point:
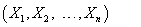
where
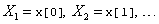
float xdata[]
(Input)
Array of size n * max(d[0], …, d[n-1]) containing the
gridpoint values for the grid.
float fdata[]
(Input)
Array of length d[0]* d[1]* …* d[n-1] containing the
values of the function to be interpolated at the gridpoints.
fdata(i, j, k,
…) is the value of the function at
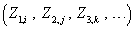
where
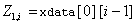
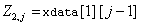
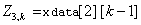
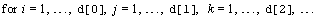
Return Value
Interpolated value of the function. If no value can be computed, NaN is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float imsl_f_spline_nd_interp (int n, int d[], float x[], float xdata[], float fdata[],
IMSL_NDEGREE, int ndeg[],
IMSL_ORDER, int nders,
IMSL_DERIV, float **deriv,
IMSL_DERIV_USER, float deriv[],
IMSL_ERR_EST, float *error,
0)
Optional Arguments
IMSL_NDEGREE, int ndeg[]
(Input)
Array of length n containing the
degree of polynomial interpolation to be used in each dimension. ndeg[i] must be less than or
equal to 15.
Default: ndeg[i] = 5, for
i = 0, …, n-1.
IMSL_ORDER, int nders
(Input)
Maximum order of derivatives to be computed with respect to each
variable. nders cannot be larger
than max (7- n, 2). All
partial derivatives up to and including order nders are returned in
each of the n
dimensions. See deriv for more
details.
Default: nders = 0.
IMSL_DERIV,
float **deriv
(Output)
Address of a pointer to an internally allocated n dimensional
array, dimensioned (nders
+1) × (nders
+1) × …, containing derivative estimates at the interpolation point.
deriv [i] [j] … will hold an
estimate of the derivative with respect to x1 i
times, and with respect to x2 j
times, etc. where i = 0, …, nders,
j = 0, …, nders, ….
The 0-th
derivative means the function value, thus, deriv[0][0] … = imsl_f_spline_nd_interp.
IMSL_DERIV_USER,
float deriv[]
(Output)
Storage for deriv is provided by
the user. See IMSL_DERIV.
IMSL_ERR_EST,
float *error
(Output)
Estimate of the error.
Description
The function imsl_f_spline_nd_interp interpolates a function of up to 7 variables, defined on a (possibly nonuniform) grid. It fits a polynomial of up to degree 15 in each variable through the grid points nearest the interpolation point. Approximations of partial derivatives are calculated, if requested. If derivatives are desired, high precision is strongly recommended. For more details, see Krogh (1970).
Example
The 3D function f(x, y, z) = exp(x + 2y + 3z), defined on a 20 by 30 by 40 uniform grid, is interpolated together with several partial derivatives.
#include <imsl.h>
#include <stdio.h>
#include <math.h>
#define N 3
#define ND1 20
#define ND2 30
#define ND3 40
#define NDERS 1
int main() {
char order[3];
int i, j, k, ndeg[N], d[N], nders=NDERS;
float xdata[N][ND3], fdata[ND1][ND2][ND3], x[N], xx, yout, yy,
zz, derout[NDERS+1][NDERS+1][NDERS+1], error, relerr, tr;
d[0] = ND1;
d[1] = ND2;
d[2] = ND3;
/*
* 20 by 30 by 40 uniform grid used for
* interpolation of F(x,y,z) = exp(x+2*y+3*z)
*/
ndeg[0] = 8;
ndeg[1] = 7;
ndeg[2] = 9;
for (i=0; i < ND1; i++)
xdata[0][i] = 0.05*(i);
for (j=0; j < ND2; j++)
xdata[1][j] = 0.03*(j);
for (k=0; k < ND3; k++)
xdata[2][k] = 0.025*(k);
for (i=0; i < ND1; i++) {
for (j=0; j < ND2; j++) {
for (k=0; k < ND3; k++) {
xx = xdata[0][i];
yy = xdata[1][j];
zz = xdata[2][k];
fdata[i][j][k] = exp(xx+2*yy+3*zz);
}
}
}
/* Interpolate at (0.18,0.43,0.35)*/
x[0] = 0.18;
x[1] = 0.43;
x[2] = 0.35;
yout = imsl_f_spline_nd_interp(N, d, x, &xdata[0][0],
&fdata[0][0][0],
IMSL_NDEGREE, ndeg,
IMSL_ORDER, nders,
IMSL_DERIV_USER, &derout[0][0][0],
IMSL_ERR_EST, &error, 0);
/*
* Output F,Fx,Fy,Fz,Fxy,Fxz,Fyz,Fxyz at
* interpolation point
*/
xx = x[0];
yy = x[1];
zz = x[2];
printf("EST. VALUE = %g, EST. ERROR = %g\n\n", yout, error);
printf(" Computed Der. True Der. Rel. Err\n");
for (k=0; k <= NDERS; k++) {
for (j=0; j <= NDERS; j++) {
for (i=0; i <= NDERS; i++) {
order[0] = ' ';
order[1] = ' ';
order[2] = ' ';
if (i == 1) order[0] = 'x';
if (j == 1) order[1] = 'y';
if (k == 1) order[2] = 'z';
tr = pow(2,j) * pow(3,k) * exp(xx+2*yy+3*zz);
relerr = (derout[i][j][k] - tr)/tr;
printf("F%s", order);
printf("%14.6f %14.6f %14.3e\n", derout[i][j][k],
tr, relerr);
}
}
}
}
Output
Est. Value = 8.08491, Est. Error = 4.18959e-006
Computed Der. True Der. Rel. Err
F 8.084914 8.084915 -1.180e-007
Fx 8.084922 8.084915 8.257e-007
F y 16.169794 16.169830 -2.241e-006
Fxy 16.170071 16.169830 1.486e-005
F z 24.254747 24.254745 7.864e-008
Fx z 24.253994 24.254745 -3.098e-005
F yz 48.510410 48.509491 1.895e-005
Fxyz 48.533176 48.509491 4.883e-004
Warning Errors
IMSL_ARG_TOO_BIG “nders” is too large, it has been reset to max(7-n,2).
IMSL_INTERP_OUTSIDE_DOMAIN The interpolation point is outside the domain of the table, so extrapolation is used.
Fatal Errors
IMSL_TOO_MANY_DERIVATIVES Too many derivatives requested for the polynomial degree used.
IMSL_POLY_DEGREE_TOO_LARGE One of the polynomial degrees requested is too large for the number of gridlines in that direction.
