Analyzes a completely nested random model with possibly unequal numbers in the subgroups.
Synopsis
#include <imsls.h>
float *imsls_f_anova_nested (int n_factors, int equal_option, int n_levels[], float y[], ..., 0)
The type double function is imsls_d_anova_nested.
Required Arguments
int n_factors
(Input)
Number of factors (number of subscripts) in the model, including
error.
int equal_option
(Input)
Equal numbers option.
|
equal_option |
Description |
|
0 |
Unequal numbers in the subgroups. |
|
1 |
Equal numbers in the subgroups. |
int n_levels[]
(Input)
Array with the number of levels for each factor.
If equal_option = 1, n_levels is of length n_factors and contains the number of levels for each of the factors.
Example: Suppose there are 3 factors, A, B, and C. A has two levels (A1, A2), B has 3 levels at each level of A, and C has 2 levels at each level of B. n_levels = {2,3,2} and the number of observations is nobs = 2 × 3 × 2 = 12.
|
|
A levels |
B levels |
C levels |
y indices |
|
|
1 |
1 |
1 |
0 |
|
|
|
|
2 |
1 |
|
|
|
2 |
1 |
2 |
|
|
|
|
2 |
3 |
|
|
|
3 |
1 |
4 |
|
|
|
|
2 |
5 |
|
|
2 |
1 |
1 |
6 |
|
|
|
|
2 |
7 |
|
|
|
2 |
1 |
8 |
|
|
|
|
2 |
9 |
|
|
|
3 |
1 |
10 |
|
|
|
|
2 |
11 |
|
|
|
|
|
|
|
n_levels |
2 |
3 |
2 |
|
|
nobs |
2× |
3× |
3× |
=12 |
|
|
equal_option = 1 example | |||
If equal_option = 0, n_levels contains the number of levels of each factor at each level of the factor in which it is nested.
Example: Suppose there are 3 factors, A, B, and C, with C nested in B and B nested in A. A has two levels (A1, A2), B has up to 3 levels, and C has up to 2 levels. In the equal_option = 0 case, the function needs to know explicitly how the number of levels varies throughout. As specified in the table, A has two levels (n_levels[0] = 2), B has 3 levels in level 1 of A (n_levels[1] = 3) and 2 levels in level 2 of A (n_levels[2] = 2). Similarly, factor C has 2 levels in the A1-B1 and A1-B2 combinations (n_levels[3] = 2, n_levels[4] = 2), but only 1 level in the A1-B3 combination (n_levels[5] = 1). n_levels = {2,3,2,2,2,1,1,2} and the number of observations is the sum of the number of levels in the last factor, C, nobs = 2 + 2 + 1 + 1 + 2 = 8:
|
|
A levels |
B levels |
C levels |
y indices |
|
|
1 |
1 |
1 |
0 |
|
|
|
|
2 |
1 |
|
|
|
2 |
1 |
2 |
|
|
|
|
2 |
3 |
|
|
|
3 |
1 |
4 |
|
|
2 |
1 |
1 |
5 |
|
|
|
2 |
1 |
6 |
|
|
|
|
2 |
7 |
|
|
|
|
|
|
|
n_levels |
2 |
3, 2 |
2 , 2, 1, 1, 2 |
|
|
nobs |
|
|
2 + 2 + 1 + 1 + 2 |
= 8 |
|
|
equal_option = 0 example | |||
float y[]
(Input)
Array of length NOBS containing the
responses.
Return Value
The p-value for the F-statistic, anova_table[9].
Synopsis with Optional Arguments
#include <imsls.h>
float *imsls_f_anova_nested (int n_factors, int equal_option, int n_levels[], float y[],
IMSLS_ANOVA_TABLE, float **anova_table,
IMSLS_ANOVA_TABLE_USER, float anova_table[]
IMSLS_CONFIDENCE, float confidence,
IMSLS_VARIANCE_COMPONENTS, float **variance_components,
IMSLS_VARIANCE_COMPONENTS_USER, float variance_components[],
IMSLS_EMS, float **expect_mean_sq,
IMSLS_EMS_USER, float expect_mean_sq[],
IMSLS_Y_MEANS, float **y_means,
IMSLS_Y_MEANS_USER, float y_means[],
0)
Optional Arguments
IMSLS_ANOVA_TABLE,
float **anova_table,
(Output)
Address of a pointer to an internally allocated array of
size 15 containing the analysis of variance table. The analysis of variance
statistics are as follows:
|
Element |
Analysis of Variance Statistics |
|
0 |
Degrees of freedom for the model. |
|
1 |
Degrees of freedom for error. |
|
2 |
Total (corrected) degrees of freedom. |
|
3 |
Sum of squares for the model. |
|
4 |
Sum of squares for error. |
|
5 |
Total (corrected) sum of squares. |
|
6 |
Model mean square. |
|
7 |
Error mean square. |
|
8 |
Overall F-statistic. |
|
9 |
p-value. |
|
10 |
R2 (in percent) |
|
11 |
Adjusted R2 (in percent). |
|
12 |
Estimate of the standard deviation. |
|
13 |
Overall mean of y. |
|
14 |
Coefficient of variation (in percent). |
Note that the p-value is returned as 0.0 when the value is so small that all significant digits have been lost.
IMSLS_ANOVA_TABLE_USER,
float anova_table[]
(Output)
Storage for array anova_table is provided by the user.
See IMSLS_ANOVA_TABLE.
IMSLS_CONFIDENCE,
float confidence
(Input)
Confidence level for two-sided interval estimates on the variance
components, in percent. confidence
percent confidence intervals are computed, hence, confidence must be in
the interval [0.0, 100.0). confidence often will
be 90.0, 95.0,
or 99.0. For one-sided intervals with confidence level ONECL, ONECL in the
interval [50.0,
100.0), set confidence =
100.0 - 2.0 *
(100.0 - ONECL).
Default: confidence
= 95.0.
IMSLS_VARIANCE_COMPONENTS,
float **variance_components,
(Output)
Address to a pointer to an internally allocated array.
variance_components
is an
n_factors by 9 matrix containing statistics relating to the particular
variance components in the model. Rows of variance_components
correspond to the n_factors
factors. Columns of variance_components
are as follows:
|
Column |
Description |
|
1 |
Degrees of freedom. |
|
2 |
Sum of squares. |
|
3 |
Mean squares. |
|
4 |
F–statistic. |
|
5 |
p-value for F test. |
|
6 |
Variance component estimate. |
|
7 |
Percent of variance of variance explained by variance component. |
|
8 |
Lower endpoint for a confidence interval on the variance component. |
|
9 |
Upper endpoint for a confidence interval on the variance component. |
A test for the error variance equal to zero cannot be performed. variance_components (n_factors, 4) and variance_components (n_factors, 5) are set to NaN (not a number). Note that the p-value for the F test is returned as 0.0 when the value is so small that all significant digits have been lost.
IMSLS_VARIANCE_COMPONENTS_USER,
float variance_components[]
(Output)
Storage for array variance_components is provided by the
user. See IMSLS_VARIANCE_COMPONENTS.
IMSLS_EMS,
float
**expect_mean_sq, (Output)
Address to a pointer to an
internally allocated array of length
n_factors * (n_factors +1) / 2 with
expected mean square coefficients.
IMSLS_EMS_USER,
float expect_mean_sq[],
(Output)
Storage for array expect_mean_sq is
provided by the user.
See IMSLS_EMS.
IMSLS_Y_MEANS,
float **y_means
(Output)
Address to a pointer to an internally allocated array
containing the subgroup means.
|
Equal options |
Length of y_means |
|
0 |
1 + sum of values in n_levels for the first (n_factors-1) factors |
|
1 |
1 + n_levels[0] + n_levels[0] *n_levels[1] + … + n_levels[0]* n_levels[1] * … * n_levels[n_factors – 2]. |
If the factors are labeled A, B, C, and error, the ordering of the means is grand mean, A means, AB means, and then ABC means.
IMSLS_Y_MEANS_USER,
floaty_means[]
(Output)
Storage for array y_means is provided by
the user. See
IMSLS_Y_MEANS
Description
Function imsls_f_anova_nested analyzes a nested random model with equal or unequal numbers in the subgroups. The analysis includes an analysis of variance table and computation of subgroup means and variance component estimates. Anderson and Bancroft (1952, pages 325−330) discuss the methodology. The analysis of variance method is used for estimating the variance components. This method solves a linear system in which the mean squares are set to the expected mean squares. A problem that Hocking (1985, pages 324−330) discusses is that this method can yield negative variance component estimates. Hocking suggests a diagnostic procedure for locating the cause of a negative estimate. It may be necessary to reexamine the assumptions of the model.
Example 1
An analysis of a three-factor nested random model with
equal numbers in the subgroups is performed using data discussed by Snedecor and
Cochran (1967, Table 10.16.1, pages 285−288).
The responses are calcium concentrations (in percent, dry basis) as measured in
the leaves of turnip greens. Four plants are taken at random, then three leaves
are randomly selected from each plant.
Finally, from each selected leaf two
samples are taken to determine calcium concentration. The model is
yijk = μ + αi + βij + eijk i = 1, 2, 3, 4; j = 1, 2, 3; k = 1, 2
where yijk is the calcium concentration for the k-th sample of the j-th leaf of the i-th plant, the αi’s are the plant effects and are taken to be independently distributed
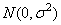
the βij’s are leaf effects each independently distributed
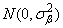
and the εijk’s are errors each independently distributed N(0, σ2). The effects are all assumed to be independently distributed. The data are given in the following table:
|
Plant |
Leaf |
Samples | |
|
1 |
1 2 3 |
3.28 3.52 2.88 |
3.09 3.48 2.80 |
|
2 |
1 2 3 |
2.46 1.87 2.19 |
2.44 1.92 2.19 |
|
3 |
1 2 3 |
2.77 3.74 2.55 |
2.66 3.44 2.55 |
|
4 |
1 2 3 |
3.78 4.07 3.31 |
3.87 4.12 3.31 |
#include <imsls.h>
int main()
{
float pvalue, *aov, *varc, *ymeans, *ems;
float y[] = {3.28, 3.09, 3.52, 3.48, 2.88, 2.80, 2.46, 2.44, 1.87,
1.92, 2.19, 2.19, 2.77, 2.66, 3.74, 3.44, 2.55, 2.55, 3.78,
3.87, 4.07, 4.12, 3.31, 3.31
};
int n_levels[] = {4, 3, 2};
char *aov_labels[] = {
"degrees of freedom for model", "degrees of freedom for error",
"total (corrected) degrees of freedom",
"sum of squares for model", "sum of squares for error",
"total (corrected) sum of squares", "model mean square",
"error mean square", "F-statistic", "p-value",
"R-squared (in percent)", "adjusted R-squared (in percent)",
"est. standard deviation of within error", "overall mean of y",
"coefficient of variation (in percent)"
};
char *ems_labels[] = {
"Effect A and Error", "Effect A and Effect B",
"Effect A and Effect A", "Effect B and Error",
"Effect B and Effect B", "Error and Error"
};
char *means_labels[] = {
"Grand mean", " A means 1", " A means 2",
" A means 3", " A means 4", "AB means 1 1",
"AB means 1 2", "AB means 1 3", "AB means 2 1",
"AB means 2 2", "AB means 2 3", "AB means 3 1",
"AB means 3 2", "AB means 3 3", "AB means 4 1",
"AB means 4 2", "AB means 4 3"
};
char *components_labels[] = {
"degrees of freedom for A", "sum of squares for A",
"mean square of A", "F-statistic for A", "p-value for A",
"Estimate of A", "Percent Variation Explained by A",
"95% Confidence Interval Lower Limit for A",
"95% Confidence Interval Upper Limit for A",
"degrees of freedom for B", "sum of squares for B",
"mean square of B", "F-statistic for B", "p-value for B",
"Estimate of B", "Percent Variation Explained by B",
"95% Confidence Interval Lower Limit for B",
"95% Confidence Interval Upper Limit for B",
"degrees of freedom for Error", "sum of squares for Error",
"mean square of Error", "F-statistic for Error",
"p-value for Error", "Estimate of Error",
"Percent Explained by Error",
"95% Confidence Interval Lower Limit for Error",
"95% Confidence Interval Upper Limit for Error"
};
pvalue = imsls_f_anova_nested(3, 1, n_levels, y,
IMSLS_ANOVA_TABLE, &aov,
IMSLS_Y_MEANS, &ymeans,
IMSLS_VARIANCE_COMPONENTS, &varc,
IMSLS_EMS, &ems,
0);
printf("pvalue = %f\n", pvalue);
imsls_f_write_matrix("* * * Analysis of Variance * * *", 15, 1, aov,
IMSLS_ROW_LABELS, aov_labels,
IMSLS_WRITE_FORMAT, "%11.4g",
0);
imsls_f_write_matrix(
"* * * Expected Mean Square Coefficients * * *",
6, 1, ems,
IMSLS_ROW_LABELS, ems_labels,
IMSLS_WRITE_FORMAT, "%6.2f",
0);
imsls_f_write_matrix("* * * Means * * *", 17, 1, ymeans,
IMSLS_ROW_LABELS, means_labels,
IMSLS_WRITE_FORMAT, "%6.2f",
0);
imsls_f_write_matrix(
"* * Analysis of Variance / Variance Components * *",
27, 1, varc,
IMSLS_ROW_LABELS, components_labels,
IMSLS_WRITE_FORMAT, "%11.4g",
0);
}
Output
pvalue = 0.000000
* * * Analysis of Variance * * *
degrees of freedom for model 11
degrees of freedom for error 12
total (corrected) degrees of freedom 23
sum of squares for model 10.19
sum of squares for error 0.07985
total (corrected) sum of squares 10.27
model mean square 0.9264
error mean square 0.006655
F-statistic 139.2
p-value 6.769e-011
R-squared (in percent) 99.22
adjusted R-squared (in percent) 98.51
est. standard deviation of within error 0.08158
overall mean of y 3.012
coefficient of variation (in percent) 2.708
* * * Expected Mean Square Coefficients * * *
Effect A and Error 1.00
Effect A and Effect B 2.00
Effect A and Effect A 6.00
Effect B and Error 1.00
Effect B and Effect B 2.00
Error and Error 1.00
* * * Means * * *
Grand mean 3.01
A means 1 3.17
A means 2 2.18
A means 3 2.95
A means 4 3.74
AB means 1 1 3.18
AB means 1 2 3.50
AB means 1 3 2.84
AB means 2 1 2.45
AB means 2 2 1.89
AB means 2 3 2.19
AB means 3 1 2.72
AB means 3 2 3.59
AB means 3 3 2.55
AB means 4 1 3.82
AB means 4 2 4.10
AB means 4 3 3.31
* * Analysis of Variance / Variance Components * *
degrees of freedom for A 3
sum of squares for A 7.56
mean square of A 2.52
F-statistic for A 7.665
p-value for A 0.009725
Estimate of A 0.3652
Percent Variation Explained by A 68.53
95% Confidence Interval Lower Limit for A 0.03955
95% Confidence Interval Upper Limit for A 5.787
degrees of freedom for B 8
sum of squares for B 2.63
mean square of B 0.3288
F-statistic for B 49.41
p-value for B 5.092e-008
Estimate of B 0.1611
Percent Variation Explained by B 30.22
95% Confidence Interval Lower Limit for B 0.06967
95% Confidence Interval Upper Limit for B 0.6004
degrees of freedom for Error 12
sum of squares for Error 0.07985
mean square of Error 0.006655
F-statistic for Error ...........
p-value for Error ...........
Estimate of Error 0.006655
Percent Explained by Error 1.249
95% Confidence Interval Lower Limit for Error 0.003422
95% Confidence Interval Upper Limit for Error 0.01813
Example 2
An analysis of a three-factor nested random model with unequal numbers in the subgroups is performed. The data are given in the following table:
|
A |
B |
C | ||
|
1 |
1 2 |
23.0 31.0 |
19.0 37.0 |
|
|
2 |
1 2 |
33.0 29.0 |
29.0 |
|
|
3 |
1 |
36.0 |
29.0 |
33.0 |
|
4 |
1 2 3 4 5 6 7 8 9 |
11.0 23.0 33.0 23.0 26.0 39.0 20.0 24.0 36.0 |
21.0 18.0 |
|
|
5 |
1 |
25.0 |
33.0 |
|
|
6 |
1 2 3 4 5 6 7 8 9 10 |
28.0 25.0 32.0 41.0 35.0 16.0 30.0 40.0 32.0 44.0 |
31.0 42.0 36.0 |
|
#include <imsls.h>
int main()
{
float *aov, *ems, *vc, *ymeans;
float y[36] = {23.0, 19.0, 31.0, 37.0,
33.0, 29.0, 29.0,
36.0, 29.0, 33.0,
11.0, 21.0,
23.0, 18.0,
33.0, 23.0, 26.0, 39.0, 20.0, 24.0, 36.0,
25.0, 33.0,
28.0, 31.0,
25.0, 42.0,
32.0, 36.0,
41.0, 35.0, 16.0, 30.0, 40.0, 32.0, 44.0
};
int nl[32] = {
6, /* Factor A */
2, 2, 1, 9, 1, 10, /* Factor B */
2, 2, /* Factor C */
2, 1,
3,
2, 2, 1, 1, 1, 1, 1, 1, 1,
2,
2, 2, 2, 1, 1, 1, 1, 1, 1, 1
};
int i, ymeans_length;
char *aov_labels[] = {
"degrees of freedom for model", "degrees of freedom for error",
"total (corrected) degrees of freedom",
"sum of squares for model", "sum of squares for error",
"total (corrected) sum of squares", "model mean square",
"error mean square", "F-statistic", "p-value",
"R-squared (in percent)", "adjusted R-squared (in percent)",
"est. standard deviation of within error",
"overall mean of y",
"coefficient of variation (in percent)"
};
char *ems_labels[] = {
"Effect A and Error", "Effect A and Effect B",
"Effect A and Effect A", "Effect B and Error",
"Effect B and Effect B", "Error and Error"
};
char *means_labels[] = {
"Grand mean", " A means 1", " A means 2",
" A means 3", " A means 4", " A means 5",
" A means 6", "AB means 1 1", "AB means 1 2",
"AB means 2 1", "AB means 2 2", "AB means 3 1",
"AB means 4 1", "AB means 4 2", "AB means 4 3",
"AB means 4 4", "AB means 4 5", "AB means 4 6",
"AB means 4 7", "AB means 4 8", "AB means 4 9",
"AB means 5 1", "AB means 6 1", "AB means 6 2",
"AB means 6 3", "AB means 6 4", "AB means 6 5",
"AB means 6 6", "AB means 6 7", "AB means 6 8",
"AB means 6 9", "AB means 6 10"
};
char *components_labels[] = {
"degrees of freedom for A", "sum of squares for A",
"mean square of A", "F-statistic for A", "p-value for A",
"Estimate of A", "Percent Variation Explained by A",
"95% Confidence Interval Lower Limit for A",
"95% Confidence Interval Upper Limit for A",
"degrees of freedom for B", "sum of squares for B",
"mean square of B", "F-statistic for B", "p-value for B",
"Estimate of B", "Percent Variation Explained by B",
"95% Confidence Interval Lower Limit for B",
"95% Confidence Interval Upper Limit for B",
"degrees of freedom for Error", "sum of squares for Error",
"mean square of Error", "F-statistic for Error",
"p-value for Error", "Estimate of Error",
"Percent Explained by Error",
"95% Confidence Interval Lower Limit for Error",
"95% Confidence Interval Upper Limit for Error"};
imsls_f_anova_nested (3, 0, nl, y,
IMSLS_ANOVA_TABLE, &aov,
IMSLS_EMS, &ems,
IMSLS_VARIANCE_COMPONENTS, &vc,
IMSLS_Y_MEANS, &ymeans,
0);
imsls_f_write_matrix("***AnalysisofVariance ***", 15, 1, aov,
IMSLS_ROW_LABELS, aov_labels,
IMSLS_WRITE_FORMAT, "%10.5f",
0);
imsls_f_write_matrix("***ExpectedMeanSquare Coefficients ***",
6, 1, ems,
IMSLS_ROW_LABELS, ems_labels,
IMSLS_WRITE_FORMAT, "%6.2f",
0);
/* sum level count for factors 1 and 2 */
ymeans_length = 1;
for (i=0; i<=6;i++) ymeans_length += nl[i];
imsls_f_write_matrix("* * * Means ***", ymeans_length, 1, ymeans,
IMSLS_ROW_LABELS, means_labels,
IMSLS_WRITE_FORMAT, "%6.2f",
0);
imsls_f_write_matrix(
"** Analysis of Variance / Variance Components **", 27, 1, vc,
IMSLS_ROW_LABELS, components_labels,
IMSLS_WRITE_FORMAT, "%10.5f",
0);
}
Output
***AnalysisofVariance ***
degrees of freedom for model 24.00000
degrees of freedom for error 11.00000
total (corrected) degrees of freedom 35.00000
sum of squares for model 1810.80591
sum of squares for error 310.16650
total (corrected) sum of squares 2120.97241
model mean square 75.45025
error mean square 28.19695
F-statistic 2.67583
p-value 0.04587
R-squared (in percent) 85.37621
adjusted R-squared (in percent) 53.46977
est. standard deviation of within error 5.31008
overall mean of y 29.52778
coefficient of variation (in percent) 17.98334
***ExpectedMeanSquare Coefficients ***
Effect A and Error 1.00
Effect A and Effect B 1.97
Effect A and Effect A 5.38
Effect B and Error 1.00
Effect B and Effect B 1.29
Error and Error 1.00
* * * Means ***
Grand mean 29.53
A means 1 27.50
A means 2 30.33
A means 3 32.67
A means 4 24.91
A means 5 29.00
A means 6 33.23
AB means 1 1 21.00
AB means 1 2 34.00
AB means 2 1 31.00
AB means 2 2 29.00
AB means 3 1 32.67
AB means 4 1 16.00
AB means 4 2 20.50
AB means 4 3 33.00
AB means 4 4 23.00
AB means 4 5 26.00
AB means 4 6 39.00
AB means 4 7 20.00
AB means 4 8 24.00
AB means 4 9 36.00
AB means 5 1 29.00
AB means 6 1 29.50
AB means 6 2 33.50
AB means 6 3 34.00
AB means 6 4 41.00
AB means 6 5 35.00
AB means 6 6 16.00
AB means 6 7 30.00
AB means 6 8 40.00
AB means 6 9 32.00
AB means 6 10 44.00
* * Analysis of Variance / Variance Components * *
degrees of freedom for A 5.00000
sum of squares for A 461.42230
mean square of A 92.28446
F-statistic for A 0.98770
p-value for A 0.46007
Estimate of A -0.21371
Percent Variation Explained by A ..........
95% Confidence Interval Lower Limit for A ..........
95% Confidence Interval Upper Limit for A ..........
degrees of freedom for B 19.00000
sum of squares for B 1349.38354
mean square of B 71.02019
F-statistic for B 2.51872
p-value for B 0.05965
Estimate of B 33.19880
Percent Variation Explained by B 54.07344
95% Confidence Interval Lower Limit for B 0.00000
95% Confidence Interval Upper Limit for B 100.58640
degrees of freedom for Error 11.00000
sum of squares for Error 310.16650
mean square of Error 28.19695
F-statistic for Error ..........
p-value for Error ..........
Estimate of Error 28.19695
Percent Explained by Error 45.92656
95% Confidence Interval Lower Limit for Error 14.14990
95% Confidence Interval Upper Limit for Error 81.28591
