Evaluates the binomial distribution function.
Synopsis
#include <imsls.h>
float imsls_f_binomial_cdf (int k, int n, float p)
The type double function is imsls_d_binomial_cdf.
Required Arguments
int k
(Input)
Argument for which the binomial distribution function is to be
evaluated.
int n
(Input)
Number of Bernoulli trials.
float p
(Input)
Probability of success on each trial.
Return Value
The probability that k or fewer successes occur in n independent Bernoulli trials, each of which has a probability p of success.
Description
The imsls_f_binomial_cdf function evaluates the distribution function of a binomial random variable with parameters n and p. It does this by summing probabilities of the random variable taking on the specific values in its range. These probabilities are computed by the recursive relationship:
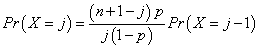
To avoid the possibility of underflow, the probabilities are computed forward from 0 if k is not greater than n × p; otherwise, they are computed backward from n. The smallest positive machine number, ɛ, is used as the starting value for summing the probabilities, which are rescaled by (1 − p)nɛ if forward computation is performed and by pnɛ if backward computation is used.
For the special case of p = 0, imsls_f_binomial_cdf is set to 1; for the case p = 1, imsls_f_binomial_cdf is set to 1 if k = n and is set to 0 otherwise.
Example
Suppose X is a binomial random variable with n = 5 and p = 0.95. In this example, the function finds the probability that X is less than or equal to 3.
#include <imsls.h>
#include <stdio.h>
int main()
{
int k = 3, n = 5;
float p = 0.95, pr;
pr = imsls_f_binomial_cdf(k,n,p);
printf("Pr(x <= %d) = %6.4f\n", k, pr);
}
Output
Pr(x <= 3) = 0.0226
Informational Errors
IMSLS_LESS_THAN_ZERO Since “k” = # is less than zero, the distribution function is set to zero.
IMSLS_GREATER_THAN_N The input argument, k, is greater than the number of Bernoulli trials, n.
