Definitions and discussions of the terms basic to this chapter can be found in Johnson and Kotz (1969, 1970a, 1970b). These are also good references for the specific distributions.
In order to keep the calling sequences simple, whenever possible, the subprograms described in this chapter are written for standard forms of statistical distributions. Hence, the number of parameters for any given distribution may be fewer than the number often associated with the distribution. For example, while a gamma distribution is often characterized by two parameters (or even a third, “location”), there is only one parameter that is necessary, the “shape”.
The “scale” parameter can be used to scale the variable to the standard gamma distribution. Also, the functions relating to the normal distribution, imsls_f_normal_cdf and imsls_f_normal_inverse_cdf, are for a normal distribution with mean equal to zero and variance equal to one. For other means and variances, it is very easy for the user to standardize the variables by subtracting the mean and dividing by the square root of the variance.
The distribution function for the (real, single-valued) random variable X is the function F defined for all real x by
F(x) = Prob(X ≤ x)
where Prob(⋅) denotes the probability of an event. The distribution function is often called the cumulative distribution function (CDF).
For distributions with finite ranges, such as the beta distribution, the CDF is 0 for values less than the left endpoint and 1 for values greater than the right endpoint. The subprograms described in this chapter return the correct values for the distribution functions when values outside of the range of the random variable are input, but warning error conditions are set in these cases.
Discrete Random Variables
For discrete distributions, the function giving the probability that the random variable takes on specific values is called the probability function, defined by
p(x) = Prob(X = x)
The “PR” functions described in this chapter evaluate probability functions.
The CDF for a discrete random variable is

where A is the set such that k ≤ x. The “DF” functions in this chapter evaluate cumulative distribution functions. Since the distribution function is a step function, its inverse does not exist uniquely.
Continuous Distributions
For continuous distributions, a probability function, as defined above, would not be useful because the probability of any given point is 0. For such distributions, the useful analog is the probability density function (PDF). The integral of the PDF is the probability over the interval, if the continuous random variable X has PDF f, then
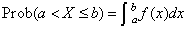
The relationship between the CDF and the PDF is
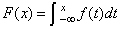 .
.
The “_cdf” functions described in this chaptersection evaluate cumulative distribution functions.
For (absolutely) continuous distributions, the value of F(x) uniquely determines x within the support of the distribution. The “_inverse_cdf” functions described in this chapter compute the inverses of the distribution functions, that is, given F(x) (called “P” for “probability”), a function such as imsls_f_beta_inverse_cdf computes x. The inverses are defined only over the open interval (0,1).
Parameter Estimation
A related task to evaluating a probability density or distribution function is to estimate the values of its parameters. For many of the distributions covered in this chapter, function imsls_f_max_likelihood_estimates provides maximum likelihood estimates of the unknown parameter values given a sample of observations.
Additional Comments
Whenever a probability close to 1.0 results from a call to a distribution function or is to be input to an inverse function, it is often impossible to achieve good accuracy because of the nature of the representation of numeric values. In this case, it may be better to work with the complementary distribution function (one minus the distribution function). If the distribution is symmetric about some point (as the normal distribution, for example) or is reflective about some point (as the beta distribution, for example), the complementary distribution function has a simple relationship with the distribution function. For example, to evaluate the standard normal distribution at 4.0, using imsls_f_normal_inverse_cdf directly, the result to six places is 0.999968. Only two of those digits are really useful, however. A more useful result may be 1.000000 minus this value, which can be obtained to six significant figures as 3.16713E-05 by evaluating imsls_f_normal_inverse_cdf at −4.0. For the normal distribution, the two values are related by Φ(x) = 1 − Φ(−x), where Φ(⋅) is the normal distribution function. Another example is the beta distribution with parameters 2 and 10. This distribution is skewed to the right, so evaluating imsls_f_beta_cdf at 0.7, 0.999953 is obtained. A more precise result is obtained by evaluating imsls_f_beta_cdf with parameters 10 and 2 at 0.3. This yields 4.72392E-5. (In both of these examples, it is wise not to trust the last digit.)
Many of the algorithms used by functions in this chaptersection are discussed by Abramowitz and Stegun (1964). The algorithms make use of various expansions and recursive relationships and often use different methods in different regions.
Cumulative distribution functions are defined for all real arguments, however, if the input to one of the distribution functions in this chaptersection is outside the range of the random variable, an error of Type 1 is issued, and the output is set to zero or one, as appropriate. A Type 1 error is of lowest severity, a “note”, and, by default, no printing or stopping of the program occurs. The other common errors that occur in the functions of this chapter are Type 2, “alert”, for a function value being set to zero due to underflow, Type 3, “warning”, for considerable loss of accuracy in the result returned, and Type 5, “terminal”, for incorrect and/or inconsistent input, complete loss of accuracy in the result returned, or inability to represent the result (because of overflow). When a Type 5 error occurs, the result is set to NaN (not a number, also used as a missing value code).
