Given an input array of deviate values, generates a canonical correlation array.
Synopsis
#include <imsls.h>
float *imsls_f_canonical_correlation (int nseq, int nvar, float devt[],..., 0)
The type double function is imsls_d_canonical_correlation.
Required Arguments
int nseq
(Input)
Number of steps in each deviate variable sequence.
int nvar
(Input)
Number of deviate variables.
float devt[]
(Input)
An array of length nseq × nvar of deviate values
containing nseq
row elements for each of nvar variables
(columns).
Return Value
An array of length nvar × nvar containing the canonical correlation array.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_canonical_correlation (int
nseq,
int
nvar,
float
devt[],
IMSLS_RETURN_USER, corr[],
0)
Optional Arguments
IMSLS_RETURN_USER,
corr[]
(Output)
User-supplied
array of length nvar × nvar containing
canonical correlation array.
Description
Function imsls_f_canonical_correlation generates a canonical correlation matrix from an arbitrarily distributed multivariate deviate sequence devt with nvar deviate variables, nseq elements in each deviate sequence, and a Gaussian Copula dependence structure.
Function imsls_f_canonical_correlation first maps each of the j = 0, ..., nvar-1 input deviate sequences devt[k = 0, ..., nseq-1][ j] into a corresponding sequence of variates, say Vkj (where variates are values of the empirical cumulative probability function, CDF(x), defined as the probability that random deviate variable X < x). The variate matrix element Vkj is then mapped into standard normal N(0,1) distributed deviates zkj using the inverse standard normal CDF imsls_f_normal_inverse_cdf(Vkj) and then the standard covariance estimator
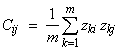
(where m = nseq and i and j have values between 1 and nvar) is used to calculate the canonical correlation matrix corr, where Ci j = corr[i-1][j-1] = the return value canonical correlation array.
If a multivariate distribution has Gaussian marginal distributions, then the standard “empirical” correlation matrix given above is “unbiased”, i.e. an accurate measure of dependence among the variables. But when the marginal distributions depart significantly from Gaussian, i.e. are skewed or flattened, then the empirical correlation may become biased. One way to remove such bias from dependence measures is to map the non-Gaussian-distributed marginal deviates to N(0,1) deviates (by mapping the non-Gaussian marginal deviates to empirically derived marginal CDF variate values, then inverting the variates to N(0,1) deviates as described above), and calculating the standard empirical correlation matrix from these N(0,1) deviates as in the equation above. The resulting “canonical correlation” matrix thereby avoids the bias that would occur if the empirical correlation matrix were extracted from the non-Gaussian marginal distributions directly.
The canonical correlation matrix may be of value in such applications as Markowitz portfolio optimization, where an unbiased measure of dependence is required to evaluate portfolio risk, defined in terms of the portfolio variance which is in turn defined in terms of the correlation among the component portfolio instruments.
The utility of the canonical correlation derives from the observation that a “copula” multivariate distribution with uniformly-distributed deviates (corresponding to the CDF probabilities associated with the marginal deviates) may be mapped to arbitrarily distributed marginals, so that an unbiased dependence estimator derived from one set of marginals N(0,1) (distributed marginals) can be used to represent the dependence associated with arbitrarily-distributed marginals. The “Gaussian Copula” (whose variate arguments are derived from N(0,1) marginal deviates) is a particularly useful structure for representing multivariate dependence.
Example: Using Gaussian Copulas to Imprint and Extract Correlation Information
This example uses function imsls_f_random_mvar_gaussian_copula to generate a multivariate sequence gcdevt whose marginal distributions are user-defined and imprinted with a user-specified input correlation matrix corrin and then uses function imsls_f_canonical_correlation to extract an output canonical correlation matrix corrout from this multivariate random sequence.
This example illustrates two useful copula related procedures. The first procedure generates a random multivariate sequence with arbitrary user-defined marginal deviates whose dependence is specified by a user-defined correlation matrix. The second procedure is the inverse of the first: an arbitrary multivariate deviate input sequence is first mapped to a corresponding sequence of empirically derived variates, i.e. cumulative distribution function values representing the probability that each random variable has a value less than or equal to the input deviate. The variates are then inverted, using the inverse standard normal CDF function, to N(0,1) deviates; and finally, a canonical covariance matrix is extracted from the multivariate N(0,1) sequence using the standard sum of products.
This example demonstrates that function imsls_f_random_mvar_gaussian_copula correctly imbeds the user-defined correlation information into an arbitrary marginal distribution sequence by extracting the canonical correlation from these sequences and showing that they differ from the original correlation matrix by a small relative error, which generally decreases as the number of multivariate sequence vectors increases.
#include <imsls.h>
#include <imsl.h>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define NVAR 3
int main()
{
int lmax=15000, i, j, k, kmax, kk;
float chol[NVAR*NVAR], gcvart[NVAR], *gcdevt, corrout[NVAR*NVAR],
relerr, arg1=10.0, arg2=15.0, rs, rs00;
float corrin[] = {
1.0, -0.9486832, 0.8164965,
-0.9486832, 1.0, -0.6454972,
0.8164965, -0.6454972, 1.0
};
printf("Off-diagonal elements of Input Correlation Matrix:\n\n");
for (i = 1; i < NVAR; i++) {
for (j = 0; j < i; j++) {
printf(" CorrIn(%d,%d) = %10.6f\n",
i, j, corrin[i*NVAR + j]);
}
}
printf("\nOff-diagonal elements of Output Correlation Matrices\n");
printf("calculated from Gaussian Copula imprinted multivariate\n");
printf("sequence:\n");
/*
* Compute the Cholesky factorization of corrin
*
* Use IMSL function imsl_f_lin_sol_posdef to generate
* the NVAR by NVAR upper triangular matrix chol from
* the Cholesky decomposition R*RT of input correlation
* matrix corrin:
*/
imsl_f_lin_sol_posdef (NVAR, corrin, NULL,
IMSL_FACTOR_USER, chol,
IMSL_FACTOR_ONLY,
0);
kmax = lmax / 100;
for (kk = 1; kk <= 3; kk++) {
gcdevt = (float *) malloc(kmax * NVAR * sizeof(float));
printf("\n# of vectors in multivariate sequence: %7d\n\n",
kmax);
/* use Congruential RN generator, with multiplier 16807 */
imsls_random_option(1);
/* set RN generator seed to be 123457 */
imsls_random_seed_set(123457);
for (k = 0; k < kmax; k++) {
/*
* generate a NVAR-length random Gaussian Copula
* variate output vector gcvart which is uniformly
* distributed on the interval [0,1] and imprinted
* with correlation information from input Cholesky
* matrix chol:
*/
imsls_f_random_mvar_gaussian_copula(NVAR, chol,
IMSLS_RETURN_USER, gcvart,
0);
for (j = 0; j < 3; j++) {
/*
* invert Gaussian Copula probabilities to deviates
* using variable-specific inversions: j = 0: Chi
* Square; j = 1: F; j = 2: Normal(0,1); will end
* up with deviate sequences ready for mapping to
* canonical correlation matrix:
*/
if (j == 0) {
/* convert probs into ChiSquare(df=10) deviates */
gcdevt[k*NVAR + j] =
imsls_f_chi_squared_inverse_cdf(gcvart[j], arg1);
} else if (j == 1) {
/* convert probs into F(dfn=15,dfd=10) deviates */
gcdevt[k*NVAR + j] =
imsls_f_F_inverse_cdf(gcvart[j], arg2, arg1);
} else {
/*
* convert probs into Normal(mean=0,variance=1)
* deviates:
*/
gcdevt[k*NVAR + j] =
imsls_f_normal_inverse_cdf(gcvart[j]);
}
}
}
/*
* extract Canonical Correlation matrix from arbitrarily
* distributed deviate sequences gcdevt (k=1..kmax, j=1..NVAR)
* which have been imprinted with corrin (i=1..NVAR, j=1..NVAR)
* above:
*/
imsls_f_canonical_correlation(kmax, NVAR, gcdevt,
IMSLS_RETURN_USER, corrout,
0);
for (i = 1; i < NVAR; i++) {
for (j = 0; j <= i-1; j++) {
rs00 = corrin[i*NVAR + j];
rs = corrout[i*NVAR + j];
relerr = fabs((rs - rs00)/rs00);
printf(" CorrOut(%d,%d) = %10.6f; relerr = %10.6f\n",
i, j, corrout[i*NVAR + j], relerr);
}
}
free(gcdevt);
kmax *= 10;
}
}
Outputs
Off-diagonal elements of Input Correlation Matrix:
CorrIn(1,0) = -0.948683
CorrIn(2,0) = 0.816496
CorrIn(2,1) = -0.645497
Off-diagonal elements of Output Correlation Matrices
calculated from Gaussian Copula imprinted multivariate
sequence:
# of vectors in multivariate sequence: 150
CorrOut(1,0) = -0.940215; relerr = 0.008926
CorrOut(2,0) = 0.794511; relerr = 0.026927
CorrOut(2,1) = -0.616082; relerr = 0.045570
# of vectors in multivariate sequence: 1500
CorrOut(1,0) = -0.947444; relerr = 0.001306
CorrOut(2,0) = 0.808306; relerr = 0.010031
CorrOut(2,1) = -0.635650; relerr = 0.015255
# of vectors in multivariate sequence: 15000
CorrOut(1,0) = -0.948263; relerr = 0.000443
CorrOut(2,0) = 0.817261; relerr = 0.000936
CorrOut(2,1) = -0.646206; relerr = 0.001098

