Given a Cholesky factorization of a correlation matrix, generates pseudorandom numbers from a Student’s t Copula distribution.
Synopsis
#include <imsls.h>
float *imsls_f_random_mvar_t_copula (float df, int n, float chol[],..., 0)
The type double function is imsls_d_random_mvar_t_copula.
Required Arguments
float df (Input)
Degrees
of freedom. df
must be greater than 2.
int n (Input)
Number of
random numbers to generate.
float chol[] (Input)
An
array of size n × n containing the
upper-triangular Cholesky factorization of the correlation matrix of order n.
Return Value
An array of length n containing the pseudorandom numbers from a multivariate Student’s t Copula distribution.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_random_mvar_t_copula (float
df,
int n,
float chol[],
IMSLS_RETURN_USER,
r[],
0)
Optional Arguments
IMSLS_RETURN_USER,
r[]
(Output)
User-supplied
array of length n containing the
pseudorandom numbers from a multivariate Student’s t Copula
distribution.
Description
Function imsls_f_random_mvar_t_copula
generates pseudorandom numbers from a multivariate Student’s t Copula
distribution which are uniformly distributed on the interval (0,1) representing
the probabilities associated with Student’s t deviates with df degrees of freedom
imprinted with correlation information from input upper-triangular Cholesky
matrix chol. Cholesky matrix
chol is defined as the “square root” of a
user-defined correlation matrix. That is, chol is an upper triangular matrix such that the
transpose of chol times chol is the correlation matrix. First, a
length n array of independent random normal deviates
with mean 0 and variance 1 is generated, and then this deviate array is
post-multiplied by Cholesky matrix chol. Each of the n
elements of the resulting vector of Cholesky-imprinted random deviates is then
divided by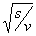
, where 
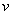= df
and s is a random deviate taken from a chi-squared distribution with
df
degrees of freedom. Each element of the Cholesky-imprinted standard normal
N(0,1) array is a linear combination of normally distributed random numbers and
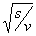is therefore itself normal, and the division of each element by insures that each element of
the resulting array is Student’s t distributed. Finally, each
element of the Cholesky-imprinted Student’s t array is mapped to an
output probability using the Student’s t cumulative distribution function
(CDF) with df
degrees of freedom.
Random deviates from arbitrary marginal distributions which are imprinted with the correlation information contained in Cholesky matrix chol can then be generated by inverting the output probabilities using user-specified inverse CDF functions.
Example: Using Student’s t Copulas to Imprint and Extract Correlation Information
This example uses function imsls_f_random_mvar_t_copula to generate a multivariate sequence tcdevt whose marginal distributions are user-defined and imprinted with a user-specified input correlation matrix corrin and then uses function imsls_f_canonical_correlation to extract an output canonical correlation matrix corrout from this multivariate random sequence.
This example illustrates two useful copula related procedures. The first procedure generates a random multivariate sequence with arbitrary user-defined marginal deviates whose dependence is specified by a user-defined correlation matrix. The second procedure is the inverse of the first: an arbitrary multivariate deviate input sequence is first mapped to a corresponding sequence of empirically derived variates, i.e. cumulative distribution function values representing the probability that each random variable has a value less than or equal to the input deviate. The variates are then inverted, using the inverse standard normal CDF function, to N(0,1) deviates; and finally, a canonical covariance matrix is extracted from the multivariate N(0,1) sequence using the standard sum of products.
This example demonstrates that function imsls_f_random_mvar_t_copula correctly imbeds the user-defined correlation information into an arbitrary marginal distribution sequence by extracting the canonical correlation from these sequences and showing that they differ from the original correlation matrix by a small relative error.
Recall that a Gaussian Copula array sequence, whose probabilities are mapped directly from Cholesky-imprinted N(0,1) deviates, has the property that the relative error between the input and output correlation matrices generally decreases as the number of multivariate sequence vectors increases. This is understandable because the correlation imprinting and extraction processes both act upon N(0,1) marginal distributions, and one would expect that a larger sample would therefore result in more accurate imprinting and extraction of correlation information.
In contrast, the imprinting of correlation information onto the Student’s t vector sequence is accomplished by imprinting onto an N(0,1) array and then dividing the array components by a scaled chi-squared random deviate, thereby introducing noise into the imprinting process. (An array of Student’s t deviates cannot be Cholesky-imprinted directly, because a linear combination of Student’s t deviates is not Student’s t distributed.) A larger sample would thus contain additional correlation information and additional noise, so the accuracy would be expected to plateau. This is illustrated in the example below, which should be compared with the Gaussian Copula example given for CNL function imsls_f_random_mvar_gaussian_copula.
#include <imsls.h>
#include <imsl.h>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define NVAR 3
int main()
{
int lmax=15000, i, j, k, kmax, kk;
float chol[NVAR*NVAR], tcvart[NVAR], *tcdevt, corrout[NVAR*NVAR],
df=5.0, relerr, arg1=10.0, arg2=15.0, rs, rs00;
float corrin[] = {
1.0, -0.9486832, 0.8164965,
-0.9486832, 1.0, -0.6454972,
0.8164965, -0.6454972, 1.0
};
printf("Off-diagonal elements of Input Correlation Matrix:\n\n");
for (i = 1; i < NVAR; i++) {
for (j = 0; j < i; j++) {
printf(" CorrIn(%d,%d) = %10.6f\n",
i, j, corrin[i*NVAR + j]);
}
}
printf("\n Degrees of freedom df = %6.2f\n", df);
printf("\n Imprinted random sequences distributions:");
printf("\n 1: Chi, 2: F, 3: Normal;\n");
printf("\nOff-diagonal elements of Output Correlation Matrices\n");
printf("calculated from Student's t Copula imprinted\n");
printf("multivariate sequence:\n");
/*
* Compute the Cholesky factorization of corrin
*
* Use IMSL function imsl_f_lin_sol_posdef to generate
* the NVAR by NVAR upper triangular matrix chol from
* the Cholesky decomposition R*RT of input correlation
* matrix corrin:
*/
imsl_f_lin_sol_posdef (NVAR, corrin, NULL,
IMSL_FACTOR_USER, chol,
IMSL_FACTOR_ONLY,
0);
kmax = lmax / 100;
for (kk = 1; kk <= 3; kk++) {
tcdevt = (float *) malloc(kmax * NVAR * sizeof(float));
printf("\n# of vectors in multivariate sequence: %7d\n\n",
kmax);
/* use Congruential RN generator, with multiplier 16807 */
imsls_random_option(1);
/* set RN generator seed to be 123457 */
imsls_random_seed_set(123457);
for (k = 0; k < kmax; k++) {
/*
* generate a NVAR-length random Student's t Copula
* variate output vector tcvart which is uniformly
* distributed on the interval [0,1] and imprinted
* with correlation information from input Cholesky
* matrix chol:
*/
imsls_f_random_mvar_t_copula(df, NVAR, chol,
IMSLS_RETURN_USER, tcvart,
0);
for (j = 0; j < 3; j++) {
/*
* invert Student's t Copula probabilities to
* deviates using variable-specific
* inversions: j = 0: Chi Square; j = 1: F;
* j = 2: Normal(0,1); will end up with deviate
* sequences ready for mapping to canonical
* correlation matrix:
*/
if (j == 0) {
/* convert probs into ChiSquare(df=10) deviates */
tcdevt[k*NVAR + j] =
imsls_f_chi_squared_inverse_cdf(tcvart[j], arg1);
} else if (j == 1) {
/* convert probs into F(dfn=15,dfd=10) deviates */
tcdevt[k*NVAR + j] =
imsls_f_F_inverse_cdf(tcvart[j], arg2, arg1);
} else {
/*
* convert probs into Normal(mean=0,variance=1)
* deviates:
*/
tcdevt[k*NVAR + j] =
imsls_f_normal_inverse_cdf(tcvart[j]);
}
}
}
/*
* extract Canonical Correlation matrix from arbitrarily
* distributed deviate sequences tcdevt (k=1..kmax, j=1..NVAR)
* which have been imprinted with corrin (i=1..NVAR, j=1..NVAR)
* above:
*/
imsls_f_canonical_correlation (kmax, NVAR, tcdevt,
IMSLS_RETURN_USER, corrout,
0);
for (i = 1; i < NVAR; i++) {
for (j = 0; j <= i-1; j++) {
rs00 = corrin[i*NVAR + j];
rs = corrout[i*NVAR + j];
relerr = fabs((rs - rs00)/rs00);
printf(" CorrOut(%d,%d) = %10.6f; relerr = %10.6f\n",
i, j, corrout[i*NVAR + j], relerr);
}
}
free (tcdevt);
kmax *= 10;
}
}
Output
Off-diagonal elements of Input Correlation Matrix:
CorrIn(1,0) = -0.948683
CorrIn(2,0) = 0.816496
CorrIn(2,1) = -0.645497
Degrees of freedom df = 5.00
Imprinted random sequences distributions:
1: Chi, 2: F, 3: Normal;
Off-diagonal elements of Output Correlation Matrices
calculated from Student's t Copula imprinted
multivariate sequence:
# of vectors in multivariate sequence: 150
CorrOut(1,0) = -0.953573; relerr = 0.005154
CorrOut(2,0) = 0.774720; relerr = 0.051166
CorrOut(2,1) = -0.621418; relerr = 0.037303
# of vectors in multivariate sequence: 1500
CorrOut(1,0) = -0.944316; relerr = 0.004603
CorrOut(2,0) = 0.810164; relerr = 0.007756
CorrOut(2,1) = -0.636348; relerr = 0.014174
# of vectors in multivariate sequence: 15000
CorrOut(1,0) = -0.946770; relerr = 0.002017
CorrOut(2,0) = 0.808564; relerr = 0.009715
CorrOut(2,1) = -0.636321; relerr = 0.014216
