Estimates missing values in a time series.
Synopsis
#include <imsls.h>
float *imsls_f_estimate_missing(int n_obs, int tpoints[], float z[],…,0)
The type double function is imsls_d_estimate_missing.
Required Arguments
int n_obs
(Input)
Number of non-missing observations in the
time series. The time series must not contain gaps with more than 3 missing
values.
int tpoints[] (Input)
Vector of length
n_obs containing
the time points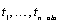 
at which the time series values
were observed. The time points must be in strictly increasing order. Time points
for missing values must lie in the open interval 
.
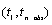float z[] (Input)
Vector
of length n
obs containing the time series values. The values must be ordered in
accordance with the values in vector tpoints. It is assumed
that the time series after estimation of missing values contains values at
equidistant time points where the distance between two consecutive time points
is one. If the non-missing time series values are observed at time points 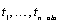, then missing values between 
and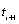 
, 
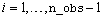, exist if 
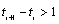. The size of the gap between and 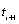is then 
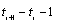. The total length of the time series
with non-missing and estimated missing values is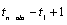 
, or tpoints[n_obs-1]-tpoints[0]+1.
Return Value
Pointer to an array of length (tpoints[n_obs-1]-tpoints[0]+1) containing the time series together with estimates for the missing values. If an error occurred, NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_estimate_missing (int
n_obs, int
tpoints[],
float
z[],
IMSLS_METHOD,
int
method,
IMSLS_MAX_LAG,
int
maxlag,
IMSLS_NTIMES,
int
*ntimes,
IMSLS_MEAN_ESTIMATE,
float
mean_estimate,
IMSLS_RELATIVE_ERROR,
float
relative_error,
IMSLS_MAX_ITERATIONS,
int
max_iterations,
IMSLS_TIMES_ARRAY,
int
**times,
IMSLS_TIMES_ARRAY_USER,
int
times[],
IMSLS_MISSING_INDEX,
int
**missing_index,
IMSLS_MISSING_INDEX_USER,
int
missing_index[],
IMSLS_RETURN_USER,
float u_z[],
0)
Optional Arguments
IMSLS_METHOD, int
method
(Input)
The method used for estimating the missing values:
|
0 |
Use median. |
|
1 |
Use cubic spline interpolation. |
|
2 |
Use one-step-ahead forecasts from an AR(1) model. |
|
3 |
Use one-step-ahead forecasts from an AR(p) model. |
Default: method = 3
If
method = 2 is
chosen, then all values of gaps beginning at time points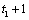 
or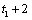 
are estimated by method 0. If method = 3 is chosen and the
first gap starts at 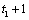, then the values of this gap are
also estimated by method 0. If the
length of the series before a gap, denoted len, is greater than 1
and less than 2
maxlag, then maxlag is reduced
to len/2 for the
computation of the missing values within this gap.
IMSLS_MAX_LAG,
int maxlag
(Input)
Maximum lag number
when method
= 3 was
chosen.
Default: maxlag = 10
IMSLS_NTIMES, int
*ntimes
(Output)
Number of elements in the time series with estimated missing
values. Note that ntimes =
tpoints[n_obs-1]-tpoints[0]+1.
IMSLS_MEAN_ESTIMATE,
float mean_estimate
(Input)
Estimate of the
mean of the time series.
IMSLS_RELATIVE_ERROR,
float relative_error
(Input)
Stopping criterion for use in the nonlinear equation solver
used by method 2.
Default: relative_error = 100
× imsls_f_machine(4) for
single
precision, relative_error = 100
× imsls_d_machine(4) for
double precision..
IMSLS_MAX_ITERATIONS,
int max_iterations
(Input)
Maximum number of iterations allowed in the nonlinear
equations solver used by method 2.
Default: max_iterations = 200.
IMSLS_TIMES_ARRAY,
int **times
(Output)
Address of a pointer to an internally allocated array of
length
ntimes = tpoints[n_obs-1]-tpoints[0]+1 containing the
time points of the time series with estimates for the missing values.
IMSLS_TIMES_ARRAY_USER,
int times[]
(Output)
Storage for array times is provided by the user. See IMSLS_TIMES_ARRAY.
IMSLS_MISSING_INDEX,
int
**missing_index (Output)
Address of a pointer to an internally
allocated array of length (ntimes-n_obs)
containing the indices for the missing values in array times. If ntimes-n_obs = 0, then
no missing value could be found and NULL is returned.
IMSLS_MISSING_INDEX_USER, int
missing_index[]
(Output)
Storage for array missing_index is provided by the
user. See IMSLS_MISSING_INDEX.
IMSLS_RETURN_USER,
float u_z[]
(Output)
If specified, u_z is a vector of
length tpoints[n_obs-1]-tpoints[0]+1
containing the time series values together with estimates for missing
values.
Description
Traditional time series analysis as described by Box,
Jenkins and Reinsel (1994) requires the observations made at equidistant time
points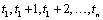 
. When observations are missing, the
problem occurs to determine suitable estimates. Function imsls_f_estimate_missing
offers 4 estimation methods:
Method 0 estimates the missing observations in
a gap by the median of the last four time series values before and the
first four values after the gap. If not enough values are available before or
after the gap then the number is reduced accordingly. This method is very
fast and simple, but its use is limited to stationary ergodic series without
outliers and level shifts.
Method 1 uses a cubic spline interpolation method to
estimate missing values. Here the interpolation is again done over the last four
time series values before and the first four values after the gap. The missing
values are estimated by the resulting interpolant. This method gives smooth
transitions across missing values.
Method 2 assumes that the time
series before the gap can be well described by an AR(1) process. If the last
observation prior to the gap is made at time point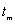 
then it uses the time series
values at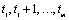 
to compute the
one-step-ahead forecast at origin 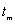. This value is taken as an estimate
for the missing value at time point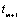 
. If the value at 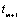is also missing then the values
at time points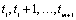 
are used to recompute the AR(1)
model, estimate the value at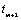 
and so on. The coefficient
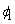in the AR(1) model is computed
internally by the method of least squares from function imsls_f_arma.
Finally, method 3 uses an AR(p) model to estimate missing
values by a one-step-ahead forecast . First, function imsls_f_auto_uni_ar,
applied to the time series prior to the missing values, is used to determine the
optimum p
from the set {0, 1, …, max_lag}
of possible values and to compute the parameters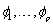 
of the resulting AR(p)
model. The parameters are estimated by the least squares method based on
Householder transformations as described in Kitagawa and Akaike (1978).
Denoting the mean of the series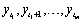 
by μ the
one-step-ahead forecast at origin ,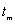 
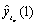, can be computed by the
formula
This value is used as an estimate for the missing value. The procedure starting with imsls_f_auto_uni_ar is then repeated for every further missing value in the gap. All four estimation methods treat gaps of missing values in increasing time order.
Example
Consider the AR(1) process
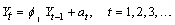
We assume that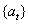 
is a Gaussian white noise process,
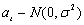. Then, 
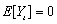and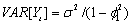 
(see Anderson, p. 174).
The time series in the code below was artificially
generated from an AR(1) process characterized by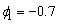 
and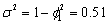 
. This process is stationary with
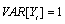. As initial value, 
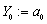was taken. The sequence 
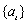was generated by a random number
generator.
From the original series, we remove the observations at time points t=130, t=140, t=141, t=160, t=175, t=176. Then, imsls_f_estimate_missing is used to compute estimates for the missing values by all 4 estimation methods available. The estimated values are compared with the actual values.
#include <stdio.h>
#include <math.h>
int main()
{
int i, j, k, maxlag = 20, times_1[200], times_2[200], ntemp,
n_obs, n_miss, ntimes, miss_ind, *times = NULL,
*missing_index = NULL;
float x_1[200], x_2[200], *result = NULL;
float y[200] = {
1.30540,-1.37166,1.47905,-0.91059,1.36191,-2.16966,3.11254,
-1.99536,2.29740,-1.82474,-0.25445,0.33519,-0.25480,-0.50574,
-0.21429,-0.45932,-0.63813,0.25646,-0.46243,-0.44104,0.42733,
0.61102,-0.82417,1.48537,-1.57733,-0.09846,0.46311,0.49156,
-1.66090,2.02808,-1.45768,1.36115,-0.65973,1.13332,-0.86285,
1.23848,-0.57301,-0.28210,0.20195,0.06981,0.28454,0.19745,
-0.16490,-1.05019,0.78652,-0.40447,0.71514,-0.90003,1.83604,
-2.51205,1.00526,-1.01683,1.70691,-1.86564,1.84912,-1.33120,
2.35105,-0.45579,-0.57773,-0.55226,0.88371,0.23138,0.59984,
0.31971,0.59849,0.41873,-0.46955,0.53003,-1.17203,1.52937,
-0.48017,-0.93830,1.00651,-1.41493,-0.42188,-0.67010,0.58079,
-0.96193,0.22763,-0.92214,1.35697,-1.47008,2.47841,-1.50522,
0.41650,-0.21669,-0.90297,0.00274,-1.04863,0.66192,-0.39143,
0.40779,-0.68174,-0.04700,-0.84469,0.30735,-0.68412,0.25888,
-1.08642,0.52928,0.72168,-0.18199,-0.09499,0.67610,0.14636,
0.46846,-0.13989,0.50856,-0.22268,0.92756,0.73069,0.78998,
-1.01650,1.25637,-2.36179,1.99616,-1.54326,1.38220,0.19674,
-0.85241,0.40463,0.39523,-0.60721,0.25041,-1.24967,0.26727,
1.40042,-0.66963,1.26049,-0.92074,0.05909,-0.61926,1.41550,
0.25537,-0.13240,-0.07543,0.10413,1.42445,-1.37379,0.44382,
-1.57210,2.04702,-2.22450,1.27698,0.01073,-0.88459,0.88194,
-0.25019,0.70224,-0.41855,0.93850,0.36007,-0.46043,0.18645,
0.06337,0.29414,-0.20054,0.83078,-1.62530,2.64925,-1.25355,
1.59094,-1.00684,1.03196,-1.58045,2.04295,-2.38264,1.65095,
-0.33273,-1.29092,0.14020,-0.11434,0.04392,0.05293,-0.42277,
0.59143,-0.03347,-0.58457,0.87030,0.19985,-0.73500,0.73640,
0.29531,0.22325,-0.60035,1.42253,-1.11278,1.30468,-0.41923,
-0.38019,0.50937,0.23051,0.46496,0.02459,-0.68478,0.25821,
1.17655,-2.26629,1.41173,-0.68331
};
int tpoints[200] = {
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,
25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,
46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,
67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,
88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,
107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,
123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,
139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,
155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,
171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,
187,188,189,190,191,192,193,194,195,196,197,198,199,200
};
n_miss = 0;
times_1[0] = times_2[0] = tpoints[0];
x_1[0] = x_2[0] = y[0];
k = 0;
for (i = 1; i < 200; i++) {
times_1[i] = tpoints[i];
x_1[i] = y[i];
/* Generate series with missing values */
if (i!=129 && i!= 139 && i!=140 && i!=159 && i!=174 && i!=175) {
k += 1;
times_2[k] = times_1[i];
x_2[k] = x_1[i];
}
}
n_obs = k + 1;
for (j=0;j<=3;j++) {
if (j <= 2)
result = imsls_f_estimate_missing(n_obs, times_2, x_2,
IMSLS_METHOD, j,
IMSLS_NTIMES, &ntimes,
IMSLS_TIMES_ARRAY, ×,
IMSLS_MISSING_INDEX, &missing_index,
0);
else
result = imsls_f_estimate_missing(n_obs, times_2, x_2,
IMSLS_METHOD, j,
IMSLS_NTIMES, &ntimes,
IMSLS_MAX_LAG, 20,
IMSLS_TIMES_ARRAY, ×,
IMSLS_MISSING_INDEX, &missing_index,
0);
if (!result) {
if (times) {
imsls_free(times);
times = NULL;
}
if (missing_index) {
imsls_free(missing_index);
missing_index = NULL;
}
return;
}
if (j == 0) printf("\nMethod: Median\n");
if (j == 1) printf("\nMethod: Cubic Spline Interpolation\n");
if (j == 2) printf("\nMethod: AR(1) Forecast\n");
if (j == 3) printf("\nMethod: AR(p) Forecast\n");
printf("ntimes = %d\n", ntimes);
printf("time\tactual\tpredicted\tdifference\n");
n_miss = ntimes-n_obs;
for (i = 0; i < n_miss; i++) {
miss_ind = missing_index[i];
printf("%d, %10.5f, %10.5f, %18.6f\n", times[miss_ind],
x_1[miss_ind], result[miss_ind],
fabs(x_1[miss_ind]-result[miss_ind]));
}
if (result) {
imsls_free(result);
result = NULL;
}
if (times) {
imsls_free(times);
times = NULL;
}
if (missing_index) {
imsls_free(missing_index);
missing_index = NULL;
}
}
}
Output
Method: Median
ntimes = 200
time actual predicted difference
130, -0.92074, 0.26132, 1.182060
140, 0.44382, 0.05743, 0.386390
141, -1.57210, 0.05743, 1.629530
160, 2.64925, 0.04680, 2.602450
175, -0.42277, 0.04843, 0.471195
176, 0.59143, 0.04843, 0.543005
Method: Cubic Spline Interpolation
ntimes = 200
time actual predicted difference
130, -0.92074, 1.54109, 2.461829
140, 0.44382, -0.40730, 0.851119
141, -1.57210, 2.49709, 4.069194
160, 2.64925, -2.94712, 5.596371
175, -0.42277, 0.25066, 0.673430
176, 0.59143, 0.38032, 0.211107
Method: AR(1) Forecast
ntimes = 200
time actual predicted difference
130, -0.92074, -0.92971, 0.008968
140, 0.44382, 1.02824, 0.584424
141, -1.57210, -0.74527, 0.826832
160, 2.64925, 1.22880, 1.420454
175, -0.42277, 0.01049, 0.433259
176, 0.59143, 0.03683, 0.554601
Method: AR(p) Forecast
ntimes = 200
time actual predicted difference
130, -0.92074, -0.86385, 0.056894
140, 0.44382, 0.98098, 0.537164
141, -1.57210, -0.64489, 0.927206
160, 2.64925, 1.18966, 1.459592
175, -0.42277, -0.00105, 0.421722
176, 0.59143, 0.03773, 0.553705
