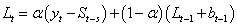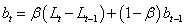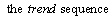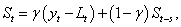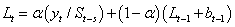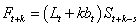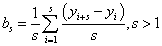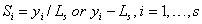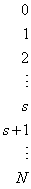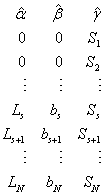hw_time_series

Chapter 8: Time Series and Forecasting > hw_time_series

hw_time_series

Calculates parameters and forecasts using the Holt-Winters Multiplicative or Additive forecasting method for seasonal data.

Synopsis

#include <imsls.h>

float *imsls_f_hw_time_series (int nobs, int nseason, float y[],..., 0)

The type double function is imsls_d_hw_time_series.

Required Arguments

int nobs (Input)
The number of equally spaced series values.

int nseason (Input)
The number of time points in a season, or the length of the season. The function requires that 2 ≤ nseason ≤ nobs unless one of the non-seasonal options is specified, in which case nseason is ignored. See the optional arguments for details.

float y[] (Input)
An array of length nobs containing the values of the time series.

Return Value

Pointer to an array of length (nobs + 1)*3 containing the values of the smoothing parameters followed by the level, trend, and seasonal component sequences. Note that if IMSLS_NONSEASONAL_TREND is specified, the array is of length (nobs + 1)*2 and if IMSLS_NONSEASONAL_CONSTANT is specified, it is of length (nobs + 1).

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_hw_time_series (int nobs, int nseason, float y[],
IMSLS_ADDITIVE, int add,
IMSLS_SERIES_INCREMENT, int incy,
IMSLS_NONSEASONAL_TREND,
IMSLS_NONSEASONAL_CONSTANT,
IMSLS_USE_PARAMS, float params[],
IMSLS_N_SAMPLE, int nsamples,
IMSLS_BOUNDS, float bounds[],
IMSLS_INIT_INPUT, int init,
IMSLS_FORECAST_CONFIDENCE, float confid,
IMSLS_RETURN_USER, float sequences[],
IMSLS_FORECASTS, int nforecasts, float **forecasts,
IMSLS_FORECASTS_USER, int nforecasts,float forecasts[],
IMSLS_SERIES_SMOOTHED, float **ysmoothed,
IMSLS_SERIES_SMOOTHED_USER, float ysmoothed[],
IMSLS_COV, float **cov,
IMSLS_COV_USER, float cov[],
IMSLS_SS_RESIDUAL, float *sumofsquares,
0)

Optional Arguments

IMSLS_ADDITIVE, int add (Input)
Specifies the use of the Multiplicative or Additive time series model. add must be 1 or 0. If add = 1 the Additive model is used.
Default: add = 0. The Multiplicative model is the default.

IMSLS_SERIES_INCREMENT, int incy (Input)
The constant stride through the series data y. The length of y must be at least (nobs-1)*|incy|+1. When incy < 0, the series is incremented in reverse order beginning at index nobs*(-incy)-1.
Default: incy = 1.

IMSLS_NONSEASONAL_TREND (Input)
Remove the seasonal component and fit only the level and trend. If present, the models involve only the level (α) and trend (β) parameters. The method is equivalent to double exponential smoothing.
Default: The method includes all three components

IMSLS_NONSEASONAL_CONSTANT (Input)
Remove the trend and the seasonal components and fit only the level. If present, the models involve only the level (α) parameter. The method is simple exponential smoothing.
Default: The method includes all three components.

IMSLS_USE_PARAMS, float params[] (Input)
An array containing the values of the smoothing parameters for the level (α), the trend (β), and the seasonal (γ) component sequences. The array should be length 3 unless IMSLS_NONSEASONAL_TREND is specified, in which case it is of length 2 containing values for level (α) and the trend (β). Likewise, if IMSLS_NONSEASONAL_CONSTANT is specified, params is of length 1 and contains the value for the level parameter (α) only.
Default: Parameter values are selected by minimizing the mean squared one step ahead forecast error.

IMSLS_N_SAMPLE, int nsamples (Input)
Number of evaluations of the residual norm that are sampled to obtain starting values for the smoothing parameters, (α, β, γ).
Default: nsamples = nobs.

IMSLS_BOUNDS, float bounds[] (Input)
An array of length 6 that contains the lower and upper bounds for each of the smoothing parameters, (α, β, γ). The three lower bounds are followed by the 3 upper bounds. Note that the lower and upper bounds must be in the interval [0,1], inclusive. The array is ignored if IMSLS_USE_PARAMS is used.
Default: Lower bounds are all 0 and upper bounds are all 1.

IMSLS_INIT_INPUT, int init (Input)
init must be 1 or 0. If init = 1, the initial values for the level, trend, and seasonal component sequences are provided in the user array, sequences. The values must be stored in rows 1, 2, …, nseason of the return array. See IMSLS_RETURN_USER and the Description section for more information.
Default: init = 0. Initial values are computed by the function.

IMSLS_FORECAST_CONFIDENCE, float confid (Input)
This value provides the confidence level to use in the calculation of the prediction intervals. If this argument is present and valid (0.0 < confid < 100.0), prediction intervals are provided for each forecast.
Default: Prediction intervals are not provided.

IMSLS_RETURN_USER, float sequences[] (Input/Output)
Storage for the return value is provided by the user. When IMSLS_INIT_INPUT is set to 1, sequences must contain initial values for the component sequences on input in rows 1, 2,…, nseason of the array. Rows 0 and nseason + 1 to nobs are ignored on input. See the Description section for the required format of the array.

IMSLS_FORECASTS, int nforecasts, float **forecasts

int nforecasts (Input)
The number of forecasts desired past the series data.

float **forecasts (Output)
Address of a pointer to an internally allocated array of length nforecasts. The value of the i-th row is the forecast (i + 1) steps past the series data. If the option IMSLS_FORECAST_CONFIDENCE is used, the array will be of length nforecasts*3 and the value of the i-th row is the forecast (i+1) steps ahead followed by the prediction interval lower and upper bounds.

IMSLS_FORECASTS_USER, int nforecasts, float forecasts[]

int nforecasts (Input)
The number of forecasts desired past the series data.

float forecasts[] (Output)
Storage for array forecasts is provided by the user. See IMSLS_FORECASTS.

IMSLS_SERIES_SMOOTHED, float **ysmoothed (Output)
The address of a pointer to the internally allocated array of length nobs containing the fitted series values.

IMSLS_SERIES_SMOOTHED_USER, float ysmoothed[] (Output)
Storage for array ysmoothed is provided by the user. See IMSLS_SERIES_SMOOTHED.

IMSLS_COV, float **cov (Output)
The address of a pointer to an internally allocated array containing the variance-covariance matrix of the smoothing parameters estimated by minimizing the mean squared forecast error. The length of the array is 3 × 3 unless IMSLS_NONSEASONAL_TREND is specified, in which case it is 2 × 2, or unless IMSLS_NONSEASONAL_CONSTANT is specified, in which case it is 1 × 1. IMSLS_COV is ignored when the option IMSLS_USE_PARAMS is present.

IMSLS_COV_USER, float cov[] (Output)
Storage for array cov is provided by the user. See IMSLS_COV.

IMSLS_SS_RESIDUAL, float *sumofsquares (Output)
The sum of squares of the one step ahead forecast errors.

Description

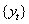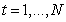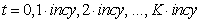Function imsls_f_hw_time_series performs the Holt-Winters forecasting method to an equally spaced time series, where N = nobs and (or where 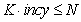and 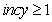). The Holt-Winters procedure fits three component sequences known as the level , the trend , and the seasonal sequence. There are two formulations, depending on whether the seasonal component of the time series is thought to be additive or multiplicative. The seasonal component depends on the length of the season, nseason = s, where s = 2,…,N.

Holt-Winters Additive Model

Holt-Winters Multiplicative Model

Note that without a seasonal component, both the additive and multiplicative formulations reduce to the same methods. (The seasonal sequence is set to 1 for the multiplicative model, and identically 0 for the additive model.)

Default Starting Values

Initial values are required for these sequences. The software allows the user code to define these initial values (see optional argument IMSLS_INIT_INPUT). If they are not provided, then the first two seasons of data are used:

The smoothing parameters (α, β, γ) are each in the interval [0,1] and can be specified by the user (see optional argument IMSLS_USE_PARAMS), or automatically set by minimizing the within sample one-step ahead mean squared forecast error. Note that this objective function is not necessarily convex and solutions will depend on starting values. See Chatfield and Yar (1988) for further discussion. Starting values for (α, β, γ) are obtained by minimizing the mean squared error over nsamples bootstrap samples of the time series. Experiments suggest that this approach helps prevent poor starting values. Note, that solutions may vary for different settings of the number of random samples, nsamples.

The return value of the imsls_hw_time_series is the array of length 3*(N + 1) = 3*(nobs + 1) containing the smoothing parameter values on the first row, followed by the calculated level, trend, and seasonal sequences. When N = nobs and s = nseason, the format of the return value is as follows:

Series Storage
Row	Value

If one of the nonseasonal options is specifed, the return value will be of length 2*(nobs + 1) or (nobs + 1) accordingly.

The variance-covariance matrix for the parameters (α, β, γ) is

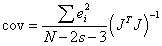
where 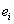is the one-step-ahead forecast error, and 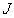is the Jacobian matrix of the series using the forecast model and calculating forecasts one step ahead of each datum. Prediction intervals are calculated following Chatfield and Yar (1991).

Example

A series of nobs = 12 seasonal data values are analysed using the Multiplicative and the Additive Holt-Winters method. The season size is nseason = 4. The objective is to predict one season ahead, nforecasts = 4 using each method. The forecasts and prediction interval lower and upper bounds are returned. The mean sum of squares of the one-step ahead forecast errors is shown to be smallest using the Multiplicative model.

#include <imsls.h>

#include <stdio.h>

#define NOBS 12

#define NSEASON 4

int main()

{

float y[NOBS]={23,25,36,31,26,28,48,36,31,42,53,43};

float *seriesm,*seriesa, *forecasts, *ysmoothed;

float ss,confidence;

int nforecasts=NSEASON,nvars=3;

/* Compute the time series and forecasts

using the Multiplicative model. */

confidence=95.0;

seriesm=imsls_f_hw_time_series(NOBS,NSEASON,y,

IMSLS_FORECAST_CONFIDENCE,confidence,

IMSLS_FORECASTS,nforecasts,&forecasts,

IMSLS_SERIES_SMOOTHED, &ysmoothed,

IMSLS_SS_RESIDUAL,&ss,

0);

imsls_f_write_matrix(" Input time series ", 1,NOBS,y,0);

imsls_f_write_matrix(" Smoothed Multiplicative series ",

1,NOBS, ysmoothed,0);

imsls_f_write_matrix(" Parameters and internal sequences ",

NOBS+1,nvars,seriesm,0);

imsls_f_write_matrix( "Multiplicative forecasts\nwith"

" 95% prediction interval",

nforecasts,3,forecasts,0);

printf("MSS - Multiplicative %3.2f \n",

ss/(float)(NOBS-NSEASON));

imsls_free(seriesm);

imsls_free(forecasts);

imsls_free(ysmoothed);

/* Compute the time series and forecasts

using the Additive model. */

seriesa=imsls_f_hw_time_series(NOBS, NSEASON, y,

IMSLS_FORECASTS,nforecasts,&forecasts,

IMSLS_SS_RESIDUAL, &ss,

IMSLS_ADDITIVE, 1,

IMSLS_FORECAST_CONFIDENCE,confidence,

IMSLS_SERIES_SMOOTHED,&ysmoothed,

0);

imsls_f_write_matrix(" Smoothed Additive series ",

1,NOBS, ysmoothed,0);

imsls_f_write_matrix(" Parameters and internal sequences ",

NOBS+1,nvars,seriesa,0);

imsls_f_write_matrix( "Additive forecasts\nwith"

" 95% prediction interval",

nforecasts,3, forecasts,0);

printf("MSS - Additive %3.2f \n",

ss/(float)(NOBS-NSEASON));

}

#undef NOBS

#undef NSEASON

Output

Input time series

1 2 3 4 5 6

23 25 36 31 26 28

7 8 9 10 11 12

48 36 31 42 53 43

Smoothed Multiplicative series

1 2 3 4 5 6

23.00 25.00 36.00 31.00 24.15 27.65

7 8 9 10 11 12

41.77 38.04 30.44 33.72 54.51 45.25

Parameters and internal sequences

1 2 3

1 0.04 1.00 0.44

2 0.00 0.00 0.80

3 0.00 0.00 0.87

4 0.00 0.00 1.25

5 28.75 1.44 1.08

6 30.28 1.53 0.83

7 31.82 1.54 0.87

8 33.55 1.73 1.33

9 35.20 1.66 1.05

10 36.89 1.68 0.83

11 38.93 2.04 0.96

12 40.93 2.00 1.31

13 42.85 1.92 1.03

Multiplicative forecasts

with 95% prediction interval

1 2 3

1 37.26 27.54 46.97

2 44.99 35.24 54.74

3 63.91 53.99 73.83

4 52.14 42.17 62.11

MSS - Multiplicative 15.35

Smoothed Additive series

1 2 3 4 5 6

23.00 25.00 36.00 31.00 23.00 26.32

7 8 9 10 11 12

38.58 38.54 34.05 35.73 56.63 43.83

Parameters and internal sequences

1 2 3

1 0.27 0.64 1.00

2 0.00 0.00 -5.75

3 0.00 0.00 -3.75

4 0.00 0.00 7.25

5 28.75 0.00 2.25

6 29.56 0.52 -3.56

7 30.52 0.81 -2.52

8 33.86 2.43 14.14

9 35.61 1.99 0.39

10 36.79 1.47 -5.79

11 39.94 2.55 2.06

12 41.51 1.92 11.49

13 43.22 1.78 -0.22

Additive forecasts

with 95% prediction interval

1 2 3

1 39.21 27.80 50.62

2 48.84 36.37 61.31

3 60.05 45.74 74.35

4 50.13 33.24 67.01

MSS - Additive 21.18

Warning Errors

IMSLS_HW_COV_NOT_EST The covariance matrix could not be estimated. The parameter estimates may be at the upper or lower bound.

Fatal Errors

IMSLS_HW_SEASON_SIZE The number for a Holt-Winters series season length must be > = 2. Input value is =#.

IMSLS_HW_SERIES_SIZE The number of observations for a Holt-Winters input series must be “nobs” > 2*“nseason”+ 3. Now have “nobs” = # and “nseason”=#.

IMSLS_HW_SERIES_SIGN The values of the input series, using the Holt-Winters Multiplicative method, must be positive. The series entry with index = # now has the non-positive value #.

Contact Support