Computes exact probabilities in a two-way contingency table using the total enumeration method.
Synopsis
#include <imsls.h>
float imsls_f_exact_enumeration (int n_rows, int n_columns, float table[], ..., 0)
The type double function is imsls_d_exact_enumeration.
Required Arguments
int n_rows (Input)
Number of rows in the table.
int n_columns (Input)
Number of columns in the table.
float table[] (Input)
Array of length n_rows × n_columns
containing the observed counts in the contingency table.
Return Value
The p-value for independence of rows and columns. The p-value represents the probability of a more extreme table where “extreme” is taken in the Neyman-Pearson sense. The p-value is “two-sided”.
Synopsis with Optional Arguments
#include <imsls.h>
float
imsls_f_exact_enumeration (int
n_rows,
int
n_columns,
float
table[],
IMSLS_PROB_TABLE,
float
*prt,
IMSLS_P_VALUE,
float
*p_value,
IMSLS_CHECK_NUMERICAL_ERROR,
float
*check,
0)
Optional Arguments
IMSLS_PROB_TABLE, float *prt
(Output)
Probablitity of the observed table occuring, given that the null
hypothesis of independent rows and columns is true.
IMSLS_P_VALUE, float *p_value
(Output)
The p-value for independence of rows and columns. The
p-value represents the probability of a more extreme table where
“extreme” is taken in the Neyman-Pearson sense. The p-value is
“two-sided”.
The p-value is also returned in functional form (see “Return Value”).
A table is more extreme if its probability (for fixed marginals) is less than or equal to prt.
IMSLS_CHECK_NUMERICAL_ERROR, float *check
(Output)
Sum of the probabilities of all tables with the same marginal
totals. Parameter check should have a value of 1.0. Deviation from 1.0 indicates
numerical error.
Description
Function imsls_f_exact_enumeration
computes exact probabilities for an
r × c contingency
table for fixed row and column marginals (a marginal is the number of counts in
a row or column), where r = n_rows
and c = n_columns.
Let fij denote the count in
row i and column j of a table, and let fi∙ and
f∙j denote the row and
column marginals. Under the hypothesis of independence, the (conditional)
probability of the fixed marginals of the observed table is given by
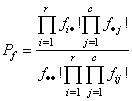
where f∙∙ is the total number of counts in the table. Pf corresponds to output argument prt.
A “more extreme” table X is defined in the probablistic sense as more extreme than the observed table if the conditional probability computed for table X (for the same marginal sums) is less than the conditional probability computed for the observed table. The user should note that this definition can be considered “two-sided” in the cell counts.
Because imsls_f_exact_enumeration used total enumeration in computing the probability of a more extreme table, the amount of computer time required increases very rapidly with the size of the table. Tables with a large total count f∙∙ or a large value of r × c should not be analyzed using imsls_f_exact_enumeration. In such cases, try using imsls_f_exact_network.
Example
In this example, the exact conditional probability for the 2 × 2 contingency table
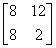
is computed.
#include <stdio.h>
#include <imsls.h>
int main()
{
float p;
float table[4] = {8, 12,
8, 2};
p = imsls_f_exact_enumeration(2, 2, table, 0);
printf("p-value = %9.4f\n", p);
}
Output
p-value = 0.0577
