Computes Fisher exact probabilities and a hybrid approximation of the Fisher exact method for a two-way contingency table using the network algorithm.
Synopsis
#include <imsls.h>
float imsls_f_exact_network (int n_rows, int n_columns, float table[], ..., 0)
The type double function is imsls_d_exact_network.
Required Arguments
int n_rows
(Input)
Number of rows in the table.
int n_columns (Input)
Number of
columns in the table.
float table[] (Input)
Array of
length n_rows × n_columns
containing the observed counts in the contingency table.
Return Value
The p-value for independence of rows and columns. The p-value represents the probability of a more extreme table where “extreme” is taken in the Neyman-Pearson sense. The p-value is “two-sided”.
Synopsis with Optional Arguments
#include <imsls.h>
float imsls_f_exact_network (int n_rows, int n_columns, float table[],
IMSLS_PROB_TABLE, float *prt,
IMSLS_P_VALUE, float *p_value,
IMSLS_APPROXIMATION_PARAMETERS, float expect, float percent, float expected_minimum,
IMSLS_NO_APPROXIMATION,
IMSLS_WORKSPACE, int factor1, int factor2, int max_attempts, int *n_attempts,
0)
Optional Arguments
IMSLS_PROB_TABLE, float *prt
(Output)
Probability of the observed table occurring given that the null
hypothesis of independent rows and columns is true.
IMSLS_P_VALUE, float *p_value
(Output)
The p-value for independence of rows and columns. The
p-value represents the probability of a more extreme table where
“extreme” is in the Neyman-Pearson sense. The p_value is
“two-sided”. The p-value is also returned in functional form (see “Return
Value”).
A table is more extreme if its probability (for fixed marginals) is less than or equal to prt.
IMSLS_APPROXIMATION_PARAMETERS, float expect, float percent,
float expected_minimum.
(Input)
Parameter expect is the expected
value used in the hybrid approximation to Fisher’s exact test algorithm for
deciding when to use asymptotic probabilities when computing path lengths.
Parameter percent is the
percentage of remaining cells that must have estimated expected values
greater than expect before
asymptotic probabilities can be used in computing path lengths. Parameter expected_minimum is
the minimum cell estimated value allowed for asymptotic chi-squared
probabilities to be used.
Asymptotic probabilities are used in computing path lengths whenever percent or more of the cells in the table have estimated expected values of expect or more, with no cell having expected value less than expected_minimum. See the “Description” section for details.
Defaults: expect = 5.0,
percent = 80.0, expected_minimum = 1.0
Note
that these defaults correspond to the “Cochran” condition.
IMSLS_NO_APPROXIMATION,
The
Fisher exact test is used. Arguments expect, percent, and expected_minimum are
ignored.
IMSLS_WORKSPACE, int factor1, int factor2, int max_attempts,
int *n_attempts
(Input/Output)
The network algorithm requires a large amount of workspace.
Some of the workspace requirements are well-defined, while most of the workspace
requirements can only be estimated. The estimate is based primarily on table
size.
Function imsls_f_exact_enumeration allocates a default amount of workspace suitable for small problems. If the algorithm determines that this initial allocation of workspace is inadaquate, the memory is freed, a larger amount of memory allocated (twice as much as the previous allocation), and the network algorithm is re-started. The algorithm allows for up to max_attempts attempts to complete the algorithm.
Because each attempt requires computer time, it is suggested that factor1 and factor2 be set to some large numbers (like 1,000 and 30,000) if the problem to be solved is large. It is suggested that factor2 be 30 times larger than factor1. Although imsls_f_exact_enumeration will eventually work its way up to a large enough memory allocation, it is quicker to allocate enough memory initially.
The known (well-defined) workspace requirements are as follows: Define f∙∙ = ∑∑fij equal to the sum of all cell frequencies in the observed table, nt = f∙∙ + 1, mx = max (n_rows, n_columns), mn = min (n_rows, n_columns), t1 = max (800 + 7mx, (5 + 2mx) (n_rows + n_columns + 1) ), and t2 = max (400 + mx, + 1, n_rows + n_columns + 1).
The following amount of integer workspace is allocated: 3mx + 2mn + t1.
The following amount of float (or double, if using imsls_d_exact_network) workspace is allocated: nt + t2.
The remainder of the workspace that is required must be estimated and allocated based on factor1 and factor2. The amount of integer workspace allocated is 6n (factor1 + factor2). The amount of real workspace allocated is n (6factor1 + 2factor2). Variable n is the index for the attempt, 1 < n ≤ max_attempts.
Defaults: factor1 = 100, factor2 = 3000, max_attempts = 10
Description
Function imsls_f_exact_network computes Fisher exact probabilities or a hybrid algorithm approximation to Fisher exact probabilities for an r × c contingency table with fixed row and column marginals (a marginal is the number of counts in a row or column), where r = n_rows and c = n_columns. Let fij denote the count in row i and column j of a table, and let fi and f∙j denote the row and column marginals. Under the hypothesis of independence, the (conditional) probability of the fixed marginals of the observed table is given by
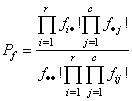
where f∙∙ is the total number of counts in the table. Pf corresponds to output argument prt.
A “more extreme” table X is defined in the probablistic sense as more extreme than the observed table if the conditional probability computed for table X (for the same marginal sums) is less than the conditional probability computed for the observed table. The user should note that this definition can be considered “two-sided” in the cell counts.
See Example 1 for a comparison of execution times for the various algorithms. Note that the Fisher exact probability and the usual asymptotic chi-squared probability will usually be different. (The network approximation is often 10 times faster than the Fisher exact test, and even faster when compared to the total enumeration method.)
Examples
Example 1
The following example demonstrates and compares the various methods of computing the chi-squared p-value with respect to accuracy and execution time. As seen in the output of this example, the Fisher exact probability and the usual asymptotic chi-squared probability (generated using function imsls_f_contingency_table) can be different. Also, note that the network algorithm with approximation can be up to 10 times faster than the network algorithm without approximation, and up to 100 times faster than the total enumeration method.
#include <stdio.h>
#include <imsls.h>
int main()
{
int n_rows = 3;
int n_columns = 5;
float p;
float table[15] = {20, 20, 0, 0, 0,
10, 10, 2, 2, 1,
20, 20, 0, 0, 0};
double a, b;
printf("Asymptotic Chi-Squared p-value\n");
p = imsls_f_contingency_table(n_rows, n_columns, table, 0);
printf("p-value = %9.4f\n", p);
printf("\nNetwork Algorithm with Approximation\n");
a = imsls_ctime();
p = imsls_f_exact_network(n_rows, n_columns, table, 0);
b = imsls_ctime();
printf("p-value = %9.4f\n", p);
printf("Execution time = %10.4f\n", b-a);
printf("\nNetwork Algoritm without Approximation\n");
a = imsls_ctime();
p = imsls_f_exact_network(n_rows, n_columns, table,
IMSLS_NO_APPROXIMATION, 0);
b = imsls_ctime();
printf("p-value = %9.4f\n", p);
printf("Execution time = %10.4f\n", b-a);
printf("\nTotal Enumeration Method\n");
a = imsls_ctime();
p = imsls_f_exact_enumeration(n_rows, n_columns, table, 0);
b = imsls_ctime();
printf("p-value = %9.4f\n", p);
printf("Execution time = %10.4f\n", b-a);
}
Output
Asymptotic Chi-Squared p-value
p-value = 0.0323
Network Algorithm with Approximation
p-value = 0.0601
Execution time = 0.0400
Network Algoritm without Approximation
p-value = 0.0598
Execution time = 0.4300
Total Enumeration Method
p-value = 0.0597
Execution time = 3.1400
Example 2
This document example demonstrates the optional keyword IMSLS_WORKSPACE and how different workspace settings affect execution time. Setting the workspace available too low results in poor performance since the algorithm will fail, re-allocate a larger amount of workspace (a factor of 10 larger) and re-start the calculations (See Test #3, for which n_attempts is returned with a value of 2). Setting the workspace available very large will provide no improvement in performance.
#include <stdio.h>
#include <imsls.h>
int main()
{
int n_rows = 3;
int n_columns = 5;
float p;
float table[15] = {20, 20, 0, 0, 0,
10, 10, 2, 2, 1,
20, 20, 0, 0, 0};
double a, b;
int i, n_attempts, simulation_size = 10;
printf("Test #1, factor1 = 1000, factor2 = 30000\n");
a = imsls_ctime();
for (i=0; i<simulation_size; i++) {
p = imsls_f_exact_network(n_rows, n_columns, table,
IMSLS_NO_APPROXIMATION,
IMSLS_WORKSPACE, 1000, 30000, 10, &n_attempts, 0);
}
b = imsls_ctime();
printf("n_attempts = %2d\n", n_attempts);
printf("Execution time = %10.4f\n", b-a);
printf("\nTest #2, factor1 = 100, factor2 = 3000\n");
a = imsls_ctime();
for (i=0; i<simulation_size; i++) {
p = imsls_f_exact_network(n_rows, n_columns, table,
IMSLS_NO_APPROXIMATION,
IMSLS_WORKSPACE, 100, 3000, 10, &n_attempts, 0);
}
b = imsls_ctime();
printf("n_attempts = %2d\n", n_attempts);
printf("Execution time = %10.4f\n", b-a);
printf("\nTest #3, factor1 = 10, factor2 = 300\n");
a = imsls_ctime();
for (i=0; i<simulation_size; i++) {
p = imsls_f_exact_network(n_rows, n_columns, table,
IMSLS_NO_APPROXIMATION,
IMSLS_WORKSPACE, 10, 300, 10, &n_attempts, 0);
}
b = imsls_ctime();
printf("n_attempts = %2d\n", n_attempts);
printf("Execution time = %10.4f\n", b-a);
}
Output
Test #1, factor1 = 1000, factor2 = 30000
n_attempts = 1
Execution time = 4.3700
Test #2, factor1 = 100, factor2 = 3000
n_attempts = 1
Execution time = 4.2900
Test #3, factor1 = 10, factor2 = 300
n_attempts = 2
Execution time = 8.3700
Warning Errors
IMSLS_HASH_TABLE_ERROR_2 The value “ldkey” = # is too small. “ldkey” is calculated as “factor1”*pow(10,”n_attempt”−1) ending this execution attempt.
IMSLS_HASH_TABLE_ERROR_3 The value “ldstp” = # is too small. “ldstp” is calculated as “factor2”*pow(10,”n_attempt”−1) ending this execution attempt.
Fatal Errors
IMSLS_HASH_TABLE_ERROR_1 The hash table key cannot be computed because the largest key is larger than the largest representable integer. The algorithm cannot proceed.
