Evaluates the hypergeometric distribution function.
Synopsis
#include <imsls.h>
float imsls_f_hypergeometric_cdf (int k, int n, int m, int l)
The type double function is imsls_d_hypergeometric_cdf.
Required Arguments
int k
(Input)
Argument for which the hypergeometric distribution function is to be
evaluated.
int n
(Input)
Sample size. Argument n must be greater than
or equal to k.
int m
(Input)
Number of defectives in the lot.
int l
(Input)
Lot size. Argument l must be greater than
or equal to n
and m.
Return Value
The probability that k or fewer defectives occur in a sample of size n drawn from a lot of size l that contains m defectives.
Description
Function imsls_f_hypergeometric_cdf evaluates the distribution function of a hypergeometric random variable with parameters n, l, and m. The hypergeometric random variable x can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability function is
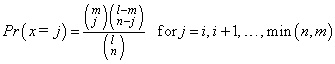
where i = max (0, n − l + m).
If k is greater than or equal to i and less than or equal to min (n, m), imsls_f_hypergeometric_cdf sums the terms in this expression for j going from i up to k; otherwise, 0 or 1 is returned, as appropriate. To avoid rounding in the accumulation, imsls_f_hypergeometric_cdf performs the summation differently, depending on whether or not k is greater than the mode of the distribution, which is the greatest integer less than or equal to (m + 1) (n + 1)/(l + 2).
Example
Suppose X is a hypergeometric random variable with n = 100, l = 1000, and m = 70. In this example, evaluate the distribution function at 7.
#include <imsls.h>
#include <stdio.h>
int main()
{
int k = 7, l = 1000, m = 70, n = 100;
float p;
p = imsls_f_hypergeometric_cdf(k,n,m,l);
printf("Pr (x <= %d) = %6.4f\n", k, p);
}
Output
Pr (x <= 7) = 0.5995
Informational Errors
IMSLS_LESS_THAN_ZERO Since “k” = # is less than zero, the distribution function is set to zero.
IMSLS_K_GREATER_THAN_N The input argument, k, is greater than the sample size.
Fatal Errors
IMSLS_LOT_SIZE_TOO_SMALL
Lot size must be greater than or equal to
n and m.
