Chapter 11: Probability Distribution Functions and Inverses > max_likelihood_estimates

max_likelihood_estimates

Calculates maximum likelihood estimates (MLE) for the parameters of one of several univariate probability distributions.

Synopsis

#include <imsls.h>

float *imsls_f_max_likelihood_estimates (int n_observations, float x[], int ipdf, ..., 0)

The type double function is imsls_d_max_likelihood_estimates.

Required Arguments

int n_observations   (Input)
Number of observations.

float x[]   (Input)
Array of length n_observations containing the data.

int ipdf   (Input)
Specifies the probability density function.

Distribution

ipdf

n_parameters

Discrete uniform

0

1

Bernoulli

1

1

Binomial (1)

2

1

Negative binomial (2)

3

1

Poisson

4

1

Geometric

5

1

Continuous uniform

6

2

Beta

7

2

Exponential

8

1

Gamma

9

2

Weibull

10

2

Rayleigh

11

1

Extreme value

12

2

Generalized extreme value

13

3

Pareto

14

2

Generalized Pareto

15

2

Normal

16

2

Log-normal

17

2

Logistic

18

2

Log-logistic

19

2

Inverse Gaussian

20

2

 

            Note:  1 - The binomial distribution requires the optional argument IMSLS_NUMBER_OF_TRIALS.

            Note:  2 - The negative binomial distribution requires the optional argument IMSLS_NUMBER_OF_FAILURES.

Return Value

A pointer to an array of length n_parameters containing the parameter values (see ipdf table above).

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_max_likelihood_estimates (int n_observations, float x[], int ipdf,
IMSLS_PRINT_LEVEL, int iprint,
IMSLS_N_PARAMETERS, int *n_parameters,
IMSLS_NUMBER_OF_TRIALS, int n_trials,
IMSLS_NUMBER_OF_FAILURES, int n_failures,
IMSLS_MLOGLIKE, float *mloglike,
IMSLS_STD_ERRORS, float **se,
IMSLS_STD_ERRORS_USER, float se[],
IMSLS_HESSIAN, float **hess,
IMSLS_HESSIAN_USER, float hess[],
IMSLS_RETURN_USER, float param[],
IMSLS_PARAM_LB, float paramlb[],
IMSLS_PARAM_UB, float paramub[],
IMSLS_INITIAL_ESTIMATES, float initial_estimates[],
IMSLS_XSCALE, float xscale[],
IMSLS_MAX_ITERATIONS, int maxit,
IMSLS_MAX_FCN, int maxfcn,
IMSLS_MAX_GRAD, int maxgrad,
0)

Optional Arguments

IMSLS_PRINT_LEVEL, int iprint   (Input)
Printing option.

 

iprint

Action

0

No printing

1

Print final results only

2

Print intermediate and final results

 

            Default:  iprint = 0.

IMSLS_N_PARAMETERS, int *n_parameters   (Output)
The number of parameters in the distribution specified by ipdf.

IMSLS_NUMBER_OF_TRIALS, int n_trials   (Input)
The number of trials.  n_trials is required for the binomial distribution, (ipdf = 2).
Default:  Not used, except for ipdf = 2.

IMSLS_NUMBER_OF_FAILURES, int n_failures   (Input)
The number of failures.  n_failures is required for the negative binomial distribution, (ipdf = 3).
Default:  Not used, except for ipdf = 3.

IMSLS_MLOGLIKE, float *mloglike   (Output)
Minus log-likelihood evaluated at the parameter estimates.

IMSLS_STD_ERRORS, float **se   (Output)
Address of a pointer to an internally allocated array of length n_parameters containing the standard errors of the parameter estimates.

IMSLS_STD_ERRORS_USER, float se[]   (Output)
Storage for array se is provided by the user. See IMSLS_STD_ERRORS.

IMSLS_HESSIAN, float **hess   (Output)
Address of a pointer to an internally allocated array of length n_parameters × n_parameters containing the Hessian matrix.

IMSLS_HESSIAN_USER, float hess[]   (Output)
Storage for array hess is provided by the user. See IMSLS_HESSIAN.

IMSLS_RETURN_USER, float param[]   (Output)
User-allocated array of length n_parameters containing the estimated parameters.

Note:  The following optional arguments are used in cases in which a quasi-Newton method is used to solve the likelihood problem (ipdf = 7,9,10,12,13,15,18,19).

IMSLS_PARAM_LB, float paramlb[]   (Input)
Array of length n_parameters containing the lower bounds of the parameters.

 

Exceptions

paramlb

Extreme value distribution (ipdf = 12)

paramlb[1] = 0.25, for the scale parameter

Generalized Pareto distribution (ipdf = 15)

paramlb[1] = -5.0, for the shape parameter

Generalized extreme value distribution (ipdf = 13)

paramlb[2] = -10.0, for the shape parameter

 

            Default:  The default lower bound depends on the range of the parameter.  That is, if the range of the parameter is positive for the desired distribution, paramlb[i] = 0.01.  If the range of the parameter is non-negative (≥ 0), then paramlb[i] = 0.0.  If the range of the parameter is unbounded, then paramlb[i] = -10000.00.

IMSLS_PARAM_UB, float paramub[]   (Input)
Array of length n_parameters containing the upper bounds of the parameters.

 

Exceptions

paramub

Generalized Pareto distribution (ipdf = 15)

paramub[1] = 5.0, for the shape parameter

Generalized extreme value distribution (ipdf = 13)

paramub[2] = 10.0, for the shape parameter

 

            Default:  paramub[i] = 10000.0.

IMSLS_INITIAL_ESTIMATES, float initial_estimates[]   (Input)
Array of length n_parameters containing the initial estimates of  the parameters.
Default:  Method of moments estimates are used for initial estimates.

IMSLS_XSCALE, float xscale[]   (Input)
Array of length n_parameters containing the scaling factors for the parameters.  xscale is used in the optimization algorithm in scaling the gradient and the distance between two points.
Default:  xscale[i] = 1.0.

IMSLS_MAX_ITERATIONS, int maxit   (Input)
Maximum number of iterations.
Default:  maxit = 100.

IMSLS_MAX_FCN, int maxfcn   (Input)
Maximum number of function evaluations.
Default:  maxfcn = 400.

IMSLS_MAX_GRAD, int maxgrad   (Input)
Maximum number of gradient evaluations.
Default:  maxgrad = 400.

Description

Function imsls_f_max_likelihood_estimates calculates maximum likelihood estimates for the parameters of a univariate probability distribution, where the distribution is one specified by ipdf and where the input data x is (assumed to be) a random sample from that distribution.

Let 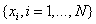represent a random sample from a probability distribution with density function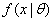, which depends on a vector 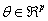containing the values of the parameters of the distribution. The values in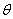 are fixed but unknown and the problem is to find an estimate for 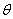 given the sample data.

The likelihood function is defined to be the product

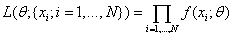
The estimator

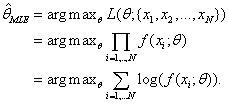
That is, the estimator that maximizes L also maximizes log L and is the maximum likelihood estimate, or MLE for .

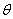The likelihood problem is in general a constrained non-linear optimization problem, where the constraints are determined by the permissible range of 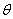.  In some situations, the problem has a closed form solution.  Otherwise, imsls_f_max_likelihood_estimates uses a quasi-Newton method to solve the likelihood problem.  If optional argument IMSLS_INITIAL_ESTIMATES is not supplied, method of moments estimates serve as starting values of the parameters.  In some cases, method of moments estimators may not exist, such as when certain moments of the true distribution do not exist; thus it is possible that the starting values are not truly method of moments estimates.

Upper and lower bounds, when needed for the optimization, have default values for each selection of ipdf (defaults will vary depending on the allowable range of the parameters).  It is possible that the optimization will fail.  In such cases, the user may try adjusting upper and lower bounds using the optional arguments IMSLS_PARAM_LB, IMSLS_PARAM_UB, or adjusting up or down the scaling factors using optional argument IMSLS_XSCALE, which can sometimes help the optimization converge.

Standard errors and covariances are supplied, in most cases, using the asymptotic properties of ML estimators.  Under some general regularity conditions, ML estimates are consistent and asymptotically normally distributed with variance-covariance equal to the inverse Fisher’s Information matrix evaluated at the true value of the parameter, :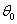

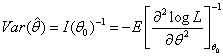
imsls_f_max_likelihood_estimates approximates the asymptotic variance using the negative inverse Hessian evaluated at the ML estimate:

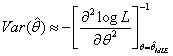
The Hessian is approximated numerically for all but a few cases where it can be determined in closed form.

In cases when the asymptotic result does not hold, standard errors may be available from the known sampling distribution. For example, the ML estimate of the Pareto distribution location parameter is the minimum of the sample.  The variance is estimated using the known sampling distribution of the minimum or first order-statistic for the Pareto distribution.

For further details regarding the properties of the estimators and the theory of the maximum likelihood method, see Kendall and Stuart (1979).  The different probability distributions have wide coverage in the statistical literature.  See Johnson and Kotz (1970a, 1970b, or later editions).

Parameter estimation (including maximum likelihoood) for the generalized Pareto distribution is studied in Hosking and Wallis (1987) and Giles and Feng (2009), and estimation for the generalized extreme value distribution is treated in Hosking, Wallis, and Wood (1985).

Remarks

1.     The location parameter is not estimated for the generalized Pareto distribution (ipdf=15). Instead, the minimum of the sample is subtracted from each observation before the estimation procedure.

2.     Only the probability of success parameter is estimated for the binomial and negative binomial distributions, (ipdf = 2,3). The number of trials and the number of failures, respectively, must be provided using optional arguments IMSLS_NUMBER_OF_TRIALS or IMSLS_NUMBER_OF_FAILURES.

3.  imsls_f_max_likelihood_estimates issues an error if missing or NaN values are encountered in the input data. Missing or NaN values should be removed before calling imsls_f_max_likelihood_estimates.

Examples

Example 1

The data are N = 100 observations generated from the logistic distribution with location parameter 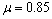 and parameter .

 

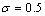#include <imsls.h>

 

int main() {

    int ipdf = 18, n_observations = 100;

    float *p_hess, *p_se, *param, mloglike;

    float x[100] = {

        2.020394,2.562315,-0.5453395,1.258546,0.7704533, 0.3662717,

        0.6885536,2.619634,-0.49581,2.972249,0.5356222,0.4262079,

        1.023666,0.8286033,1.319018,2.123659,0.3904647,-0.1196832,

        1.629261,1.069602,0.9438083,1.314796,1.404453,-0.5496156,

        0.8326595,1.570288,1.326737,0.9619384,-0.1795268,1.330161,

        -0.2916453,0.7430826,1.640854,1.582755,1.559261,0.6177695,

        1.739638,1.308973,0.568709,0.2587071,0.745583,1.003815,

        1.475413,1.444586,0.4515438,1.264374,1.788313,1.062330,

        2.126034,0.3626510,1.365612,0.5044735,2.51385,0.7910572,

        0.5932584,1.140248,2.104453,1.345562,-0.9120445,0.0006519341,

        1.049729,-0.8246097,0.8053433,1.493787,-0.5199705,2.285175,

        0.9005916,2.108943,1.40268,1.813626,1.007817,1.925250,1.037391,

        0.6767235,-0.3574937,0.696697,1.104745,-0.7691124,1.554932,

        2.090315,0.60919,0.4949385,-2.449544,0.668952,0.9480486,

        0.9908558,-1.495384,2.179275,0.1858808,-0.3715074,0.1447150,

        0.857202,1.805844,0.405371,1.425935,0.3187476,1.536181,

        -0.6352768,0.5692068,1.706736};

 

    param = imsls_f_max_likelihood_estimates(n_observations, x, ipdf,

        IMSLS_PRINT_LEVEL, 2,

        IMSLS_HESSIAN, &p_hess,

        IMSLS_STD_ERRORS, &p_se,

        IMSLS_MLOGLIKE, &mloglike,

        0);

}

Output

 

Maximum likelihood estimation for the logistic distribution

Starting Estimates:    0.90677     0.51128

 

Initial -log-likelihood:  132.75304

 

 

-log-likelihood  132.61490

 

MLE for parameter         1      0.95321

 

MLE for parameter         2      0.50953

 

Std error for parameter   1      0.08825

 

Std error for parameter   2      0.04354

 

 

          Hessian

             1            2

1       -128.5         -7.6

2         -7.6       -527.9

Example 2

The data are N = 100 observations generated from the generalized extreme value distribution with location parameter 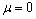, scale parameter 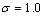, and shape parameter .

 

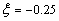#include <imsls.h>

 

int main() {

    int ipdf = 13, n_observations = 100;

    float *p_hess, *p_se, *param, mloglike;

    float x[100] = {

        0.7688048,0.1944504,-0.2992029,-0.3853738,

        -1.185593,0.3056149,-0.4407711,0.5001115,

        0.3635027,-1.058632,-0.2927695,-0.3205969,

        0.03367599,0.8850839,1.860485,0.4841038,

        0.5421101,1.883694,1.707392,0.2166106,

        1.537204,1.340291,0.4589722,1.616080,

        -0.8389288,0.7057426,1.532988,1.161350,

        0.9475416,0.4995294,-0.2392898,0.8167126,

        0.992479,-0.8357962,-0.3194499,1.233603,

        2.321555,-0.3715629,-0.1735171,0.4624801,

        -0.6249577,0.7040129,-0.3598889,0.7121399,

        -0.5178735,-1.069429,0.7169358,0.4148059,

        1.606248,-0.4640152,1.463425,0.9544342,

        -1.383239,0.1393160,0.622689,0.365793,

        0.7592438,0.810005,0.3483791,2.375727,

        -0.08124195,-0.4726068,0.1496043,0.4961212,

        1.532723,-0.1106993,1.028553,0.856018,

        -0.6634978,0.3573150,0.06391576,0.3760349,

        -0.5998756,0.4158309,-0.2832369,-1.023551,

        1.116887,1.237714,1.900794,0.6010037,

        1.599663,-0.3341879,0.5278575,0.5497694,

        0.6392933,0.592865,1.646261,-1.042950,

        -1.113611,1.229645,1.655998,0.6913992,

        0.4548073,0.4982649,-1.073640,-0.4765107,

        -0.8692533,-0.8316462,-0.03609102,0.655814};

 

    param = imsls_f_max_likelihood_estimates(n_observations,

        x, ipdf,

        IMSLS_PRINT_LEVEL, 2,

        IMSLS_HESSIAN, &p_hess,

        IMSLS_STD_ERRORS, &p_se,

        IMSLS_MLOGLIKE, &mloglike,

        0);

}

Output

 

Maximum likelihood estimation for the generalized extreme value distribution

Starting Estimates:   -0.00888     0.67451     0.00000

 

Initial -log-likelihood:  135.43817

 

 

-log-likelihood  126.09406

 

MLE for parameter         1      0.07541

 

MLE for parameter         2      0.85112

 

MLE for parameter         3     -0.27974

 

Std error for parameter   1      0.09419

 

Std error for parameter   2      0.06906

 

Std error for parameter   3      0.06603

 

 

                 Hessian

             1            2            3

1       -141.7        -53.9       -112.4

2        -53.9       -340.8       -239.7

3       -112.4       -239.7       -439.7

Warning Errors

 

IMSLS_HESSIAN_NOT_CALCULATED

The Hessian is not calculated for the requested distribution.

IMSLS_HESSIAN_NOT_USED

The Hessian is not used to calculate the standard errors of the estimates for the # distribution.

IMSLS_HESSIAN_NOT_CALC_2

For the Pareto distribution, the Hessian cannot be calculated because the parameter estimate is 0.

 

RW_logo.jpg
Contact Support