Evaluates the cumulative distribution function for the multivariate normal distribution.
Synopsis
#include <imsls.h>
float imsls_f_multivariate_normal_cdf (int k, float h[], float mean[], float sigma[], …,0)
The type double function is imsls_d_multivariate_normal_cdf.
Required Arguments
int k
(Input)
The number of variates in the multivariate normal distribution. The
number of variates must be greater than or equal to 1 and less than or equal to
1100.
float h[]
(Input)
Array of length k containing the upper
bounds for calculating the cumulative distribution function,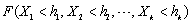 
.
float mean[]
(Input)
Array of length k containing the mean
of the multivariate normal distribution, i.e.,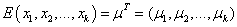 
.
float sigma[]
(Input)
Array of length k by k containing the
positive definite symmetric matrix of correlations or of variances and
covariances for the multivariate normal distribution, i.e.,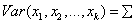 
.
Return Value
The value of the cumulative distribution function for a
multivariate normal random variable, .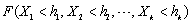
Synopsis with Optional Arguments
#include <imsls.h>
float
imsls_f_multivariate_normal_cdf (int
k, float
h[], float
mean[],
float sigma[],
IMSLS_PRINT,
IMSLS_ERR_ABS,
float err_abs,
IMSLS_ERR_REL,
float err_rel,
IMSLS_TOLERANCE, float tolerance,
IMSLS_MAX_EVALS, int max_evals,
IMSLS_RANDOM_SEED, int random_seed,
IMSLS_ERR_EST, float *err_est,
0)
Optional Arguments
IMSLS_PRINT, (Input)
Print
intermediate computations.
Default: No printing.
IMSLS_ERR_ABS,
float err_abs,
(Input)
The absolute accuracy requested for the calculated cumulative
probability.
Default: err_abs = 1.0e-3.
IMSLS_ERR_REL,
float err_rel, (Input)
The relative accuracy desired.
Default: err_rel = 1.0e-5.
IMSLS_TOLERANCE,
float tolerance,
(Input)
The minimum value for the smallest eigenvalue of sigma. If the
smallest eigenvalue is less than tolerance, then the
terminal error IMSLS_SIGMA_SINGULAR
is issued. Default: tolerance= ε, where ε is the machine
precision.
IMSLS_MAX_EVALS,
int max_evals,
(Input)
The maximum number of function evaluations allowed. If this
limit is exceeded, the IMSLS_MAX_EVALS_EXCEEDED
warning message is issued and the optimization terminates.
Default:
max_evals =
1000*k.
IMSLS_RANDOM_SEED,
int random_seed,
(Input)
The value of the random seed used for generating quadrature
points. By using different seeds on different calls to this function,
slightly different answers will be obtained in the digits beyond the estimated
error. If random_seed = 0, then
the seed is set to the value of the system clock which will automatically
generate slightly different answers for each call.
Default: random_seed =
7919.
IMSLS_ERR_EST,
float *err_est,
(Output)
The estimated error.
Description
Function
imsls_f_multivariate_normal_cdf
evaluates the cumulative distribution function F of a multivariate normal
distribution with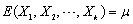 
and 
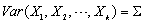. The input arrays mean
and sigma
are used as the values for μ and ∑, respectively. The formula for
the CDF calculation is given by the multiple integral described in Johnson and
Kotz (1972):
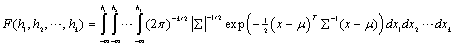
∑ must be positive definite, i.e. |∑| >0. If k = 2 or k > 2 the functions imsls_f_normal_cdf and imsls_f_bivariate_normal_cdf are used for this calculation.
In the special case of equal correlations, the above integral is transformed into a univariate integral using the transformation developed by Dunnett and Sobel(1955). This produces very accurate and fast calculations even for a large number of variates.
If k >2 and the correlations are not equal, the Cholesky decomposition transformation described by Genz (1992) is used (with permission from the author). This transforms the problem into a definite integral involving k-1 variables which is solved numerically using randomized Korobov rules if k ≤100, see Cranley and Patterson (1976) and Keast (1973); otherwise, the integral is solved using quasi-random Richtmeyer points described in Davis and Rabinowitz (1984).
Example 1
This example evaluates the cumulative distribution function for a trivariate normal random variable. There are three calculations. The first calculation is of F(1.96,1.96, 1.96) for a trivariate normal variable with μ = {0, 0, 0}, and
In this case, imsls_f_multivariate_normal_cdf calculates F(1.96, 1.96, 1.96) = 0.958179.
The second calculation involves a trivariate variable with the same correlation matrix as the first calculation but with a mean of μ = {0, 1, -1}. This is the same distribution as the first example shifted by the mean. The calculation of F(1.96, 2.96, 0.96) verifies that this probability is equal to the same value as reported for the first case.
The last calculation is the same calculation reported in Genz (1992) for a trivariate normal random variable with μ = {0, 0, 0} and
In this example the calculation of F(1, 4, 2) = 0.827985.
#include <imsls.h>
#include <stdio.h>
int main()
{
float bounds1[3] = {1.96, 1.96, 1.96};
float bounds2[3] = {1.96, 2.96, 0.96};
float bounds3[3] = {1.0, 4.0, 2.0};
float mean1[3] = {0.0, 0.0, 0.0};
float mean2[3] = {0.0, 1.0, -1.0};
float stdev1[9] = {1.0, 0.9, 0.9,
0.9, 1.0, 0.9,
0.9, 0.9, 1.0};
float stdev2[9] = {1.0, 0.6, 1.0/3.0,
0.6, 1.0, 11.0/15.0,
1.0/3.0, 11.0/15.0, 1.0};
float f;
char *fmt = {"%5.3W"};
imsls_f_write_matrix("Mean Vector", 1, 3, mean1,
IMSLS_NO_ROW_LABELS,
IMSLS_NO_COL_LABELS,
IMSLS_WRITE_FORMAT, fmt,
0);
imsls_f_write_matrix("Correlation Matrix", 3, 3,
stdev1, IMSLS_NO_ROW_LABELS,
IMSLS_NO_COL_LABELS,
IMSLS_WRITE_FORMAT, fmt,
0);
f = imsls_f_multivariate_normal_cdf(3, bounds1, mean1,
stdev1, 0);
printf("\nF(X1<%f, X2<%f, X3<%f) = %f\n\n",
bounds1[0], bounds1[1], bounds1[2], f);
imsls_f_write_matrix("Mean Vector\n", 1, 3, mean2,
IMSLS_NO_ROW_LABELS,
IMSLS_NO_COL_LABELS,
IMSLS_WRITE_FORMAT, fmt,
0);
imsls_f_write_matrix("Correlation Matrix", 3, 3,
stdev1, IMSLS_NO_ROW_LABELS,
IMSLS_NO_COL_LABELS,
IMSLS_WRITE_FORMAT, fmt,
0);
f = imsls_f_multivariate_normal_cdf(3, bounds2, mean2,
stdev1, 0);
printf("\nF(X1<%f, X2<%f, X3<%f) = %f\n",
bounds2[0], bounds2[1], bounds2[2], f);
imsls_f_write_matrix("Mean Vector", 1, 3, mean1,
IMSLS_NO_ROW_LABELS,
IMSLS_NO_COL_LABELS,
IMSLS_WRITE_FORMAT, fmt,
0);
imsls_f_write_matrix("Correlation Matrix", 3, 3, stdev2,
IMSLS_NO_ROW_LABELS,
IMSLS_NO_COL_LABELS,
IMSLS_WRITE_FORMAT, fmt,
0);
f = imsls_f_multivariate_normal_cdf(3, bounds3, mean1,
stdev2, 0);
printf("\nF(X1<%f, X2<%f, X3<%f) = %f\n",
bounds3[0], bounds3[1], bounds3[2], f);
}
Output
Mean Vector
0 0 0
Correlation Matrix
1.0 0.9 0.9
0.9 1.0 0.9
0.9 0.9 1.0
F(X1<1.960000, X2<1.960000, X3<1.960000) = 0.958179
Mean Vector
0 1 -1
Correlation Matrix
1.0 0.9 0.9
0.9 1.0 0.9
0.9 0.9 1.0
F(X1<1.960000, X2<2.960000, X3<0.960000) = 0.958179
Mean Vector
0 0 0
Correlation Matrix
1.00 0.60 0.33
0.60 1.00 0.73
0.33 0.73 1.00
F(X1<1.000000, X2<4.000000, X3<2.000000) = 0.827985
Example 2
This example illustrates the calculation of the cdf for a multivariate normal distribution with a mean of μ = {1, 0, -1, 0, 1, -1}, and a correlation matrix of
.
The optional argument IMSLS_PRINT
is used to illustrate the type of intermediate output available from this
function. This function sorts the variables by the limits for the cdf
calculation specified in x.
This improves the accuracy of the calculations, see Genz (1992). In this
case, F(X1<1, X2< 2.5, X3< 2, X4< 0.5,
X5< 0, X6< 0.8) =
0.087237 with an estimated error of
8.7e-05.
By increasing the correlation of X2 and X3 from 0.1 to 0.7, the correlation matrix becomes singular. This function checks for this condition and issues an error when sigma is not symmetric or positive definite.
#include <imsls.h>
#include <stdio.h>
int main()
{
float bounds[6] = {1.0, 2.5, 2.0, 0.5, 0.0, 0.8};
float mean[6] = {1.0, 0.0, -1.0, 0.0, 1.0, -1.0};
float s1[6*6] = {1.0, 0.1, 0.2, 0.3, 0.4, 0.0,
0.1, 1.0, 0.6, 0.1, 0.2, 0.5,
0.2, 0.6, 1.0, 0.0, 0.1, 0.2,
0.3, 0.1, 0.0, 1.0, 0.0, 0.5,
0.4, 0.2, 0.1, 0.0, 1.0, 0.3,
0.0, 0.5, 0.2, 0.5, 0.3, 1.0};
/* The following matrix is not positive definite */
float s2[6*6] = {1.0, 0.1, 0.2, 0.3, 0.4, 0.0,
0.1, 1.0, 0.6, 0.7, 0.2, 0.5,
0.2, 0.6, 1.0, 0.0, 0.1, 0.2,
0.3, 0.7, 0.0, 1.0, 0.0, 0.5,
0.4, 0.2, 0.1, 0.0, 1.0, 0.3,
0.0, 0.5, 0.2, 0.5, 0.3, 1.0};
float f, err;
int i, k=6;
f = imsls_f_multivariate_normal_cdf(k, bounds, mean, s1,
IMSLS_PRINT,
IMSLS_ERR_EST, &err,
0);
printf("F(X1<%2.1f, X2<%2.1f, X3<%2.1f, ",
bounds[0], bounds[1], bounds[2]);
printf("X4<%2.1f, X5<%2.1f, X6<%2.1f) = %f\n",
bounds[3], bounds[4], bounds[5], f);
printf("Estimated Error = %g\n", err);
/* example of error message when sigma is not positive definite */
f = imsls_f_multivariate_normal_cdf(k, bounds, mean, s2,
IMSLS_ERR_EST, &err,
0);
}
Output
Original H Limits
1.0 2.5 2.0 0.5 0.0 0.8
Original Sigma Matrix
1.0 0.1 0.2 0.3 0.4 0.0
0.1 1.0 0.6 0.1 0.2 0.5
0.2 0.6 1.0 0.0 0.1 0.2
0.3 0.1 0.0 1.0 0.0 0.5
0.4 0.2 0.1 0.0 1.0 0.3
0.0 0.5 0.2 0.5 0.3 1.0
Sorted Sigma Matrix
1.0 0.3 0.4 0.0 0.1 0.2
0.3 1.0 0.0 0.5 0.1 0.0
0.4 0.0 1.0 0.3 0.2 0.1
0.0 0.5 0.3 1.0 0.5 0.2
0.1 0.1 0.2 0.5 1.0 0.6
0.2 0.0 0.1 0.2 0.6 1.0
Eigenvalues of Sigma
eigenvalue[0] = 2.215651
eigenvalue[1] = 1.256233
eigenvalue[2] = 1.165661
eigenvalue[3] = 0.843083
eigenvalue[4] = 0.324266
eigenvalue[5] = 0.195106
Condition Number of Sigma = 7.327064
Cholesky Decomposition of Sorted Sigma Matrix
1.000 0.300 0.400 0.000 0.100 0.200
0.300 0.954 -0.126 0.524 0.073 -0.063
0.400 -0.126 0.908 0.403 0.186 0.013
0.000 0.524 0.403 0.750 0.515 0.303
0.100 0.073 0.186 0.515 0.827 0.515
0.200 -0.063 0.013 0.303 0.515 0.774
Prob. = 0.0872375 Error = 3.10012e-005
F(X1<1.0, X2<2.5, X3<2.0, X4<0.5, X5<0.0, X6<0.8) = 0.087237
Estimated Error = 3.10012e-005
eigenvalue[0] = 2.477894
eigenvalue[1] = 1.250438
eigenvalue[2] = 1.039730
eigenvalue[3] = 0.854005
eigenvalue[4] = 0.382186
eigenvalue[5] = -0.004253
*** FATAL Error IMSLS_SIGMA_SINGULAR
from
***
imsls_f_multivariate_normal_cdf.
*** "sigma" is not positive definite. Its smallest eigenvalue is
*** "e[5]"=-4.252925e-003 which is less than
*** "tolerance"=1.192093e-007.
Warning Errors
IMSLS_MAX_EVALS_EXCEEDED The maximum number of iterations for the CDF calculation has exceeded max_evals. Required accuracy may not have been achieved.
Fatal Errors
IMSLS_SIGMA_SINGULAR “sigma” is not positive definite. Its smallest eigenvalue is “e[#]”=#, which is less than “tolerance” = #.
