Evaluates the inverse of the standard normal (Gaussian) distribution function.
Synopsis
#include <imsls.h>
float imsls_f_normal_inverse_cdf (float p)
The type double function is imsls_d_normal_inverse_cdf.
Required Arguments
float p
(Input)
Probability for which the inverse of the normal distribution function
is to be evaluated. Argument p must be in the open
interval (0.0, 1.0).
Return Value
The inverse of the normal distribution function evaluated at p. The probability that a standard normal random variable takes a value less than or equal to imsls_f_normal_inverse_cdf is p.
Description
Function imsls_f_normal_inverse_cdf evaluates the inverse of the distribution function, Φ, of a standard normal (Gaussian) random variable, imsls_f_normal_inverse_cdf(p) = Φ−1(x), where
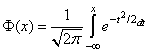
The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x. The standard normal distribution has a mean of 0 and a variance of 1.
Function imsls_f_normal_inverse_cdf is evaluated by use of minimax rational-function approximations for the inverse of the error function. General descriptions of these approximations are given in Hart et al. (1968) and Strecok (1968). The rational functions used in imsls_f_normal_inverse_cdf are described by Kinnucan and Kuki (1968).
Example
This example computes the point such that the probability is 0.9 that a standard normal random variable is less than or equal to this point.
#include <imsls.h>
#include <stdio.h>
int main()
{
float p = 0.9, x;
x = imsls_f_normal_inverse_cdf(p);
printf("The %2.0fth percentile of a standard normal is "
"%6.4f.\n", p*100.0, x);
}
Output
The 90th percentile of a standard normal is 1.2816.
