Classifies unknown patterns using a previously trained Naive Bayes classifier. The classifier is contained in an Imsls_f_nb_classifier data structure, which is optional output from imsls_f_naive_bayes_trainer.
Synopsis
#include <imsls.h>
int
*imsls_f_naive_bayes_classification (
Imsls_f_nb_classifier
*nb_classifier,
int n_patterns, …,
0)
The type double function is imsls_d_naive_bayes_classification.
Required Arguments
Imsls_f_nb_classifier
*nb_classifier
(Input)
Pointer to a structure of the type Imsls_f_nb_classifier
from imsls_f_naive_bayes_trainer.
int n_patterns
(Input)
Number of patterns to classify.
Return Value
Pointer to an array of size n_patterns containing the predicted classification associated with each input pattern.
Synopsis with Optional Arguments
#include <imsls.h>
int *imsls_f_naive_bayes_classification (Imsls_f_nb_classifier nb_classifier, int n_patterns,
IMSLS_NOMINAL, int nominal[],
IMSLS_CONTINUOUS, float continuous[],
IMSLS_PRINT_LEVEL, int print_level,
IMSLS_USER_PDF, float pdf(),
IMSLS_USER_PDF_WITH_PARMS, float pdf(), void *parms,
IMSLS_PREDICTED_CLASS_PROB, float **pred_class_prob,
IMSLS_PREDICTED_CLASS_PROB_USER, float pred_class_prob[],
IMSLS_RETURN_USER, int classification[],
0)
Optional Arguments
IMSLS_NOMINAL,
int nominal[]
(Input)
nominal is an array of
size n_patterns by nb_classifier->n_nominal
containing values for the nominal input attributes. The i-th row
contains the nominal input attributes for the i-th pattern. The
j-th column of this matrix contains the classifications for the
j-th nominal attribute. They must be encoded with integers starting
from 0 to nb_classifier->n_categories[i]-1.
Any value outside this range is treated as a missing value. If nb_classifier->n_nominal=0, this
array is ignored.
IMSLS_CONTINUOUS, float continuous[]
(Input)
continuous is an array
of size n_patterns by nb_classifier->n_continuous
containing values for the continuous input attributes. The i-th row
contains the input attributes for the i-th training pattern.
The j-th column of this matrix contains the values for the j-th
continuous attribute. Missing values should be set equal to imsls_f_machine(6)=NaN.
Patterns with missing values are still used to train the classifier unless the
IMSLS_IGNORE_MISSING_VALUES
option is supplied. If nb_classifier->n_continuous=0, this
matrix is ignored.
IMSLS_PRINT_LEVEL,
int
print_level (Input)
Print levels for printing data warnings and final
results. print_level should be
set to one of the following values:
|
print_level |
Description |
|
IMSLS_NONE |
Printing of data warnings and final results is suppressed. |
|
IMSLS_FINAL |
Prints final summary of Naive Bayes classifier training. |
|
IMSLS_DATA_WARNINGS |
Prints information about missing values and PDF calculations equal to zero. |
|
IMSLS_TRACE_ALL |
Prints final summary plus all data warnings associated with missing values and PDF calculations equal to zero. |
Default: IMSLS_NONE.
IMSLS_USER_PDF,
float pdf(int index[],
float
x,) (Input)
The
user-supplied probability density function and parameters used to calculate
the conditional probability density for continuous input attributes is required
when the classifier was trained with selected_pdf[i]= IMSLS_USER.
When
pdf is called,
x will equal
continuous[i*n_continuous+j],
and index will
contain the following values for i,
j, and k:
|
Value | |
|
index[0] |
i = pattern index |
|
index[1] |
j = attribute index |
|
index[2] |
k = target classification |
The pattern index
ranges from 0 to n_patterns-1 and
identifies the pattern index for x. The attributes index ranges from 0 to
n_categories[i]-1, and
k=classification[i].
This argument is ignored if n_continuous = 0. By default the
Gaussian PDF is used for calculating the conditional probability densities using
either the means and variances calculated from the training patterns or those
supplied in IMSLS_GAUSSIAN_PDF.
IMSLS_USER_PDF_WITH_PARMS,
float pdf(int index[], float x, void *parms),
void *parms, (Input)
The
user-supplied probability density function and parameters used to calculate the
conditional probability density for continuous input attributes is required when
selected_pdf[i]=
IMSLS_USER. PDF also accepts a
pointer to parms supplied by the user. The parameters pointed to by parms
are passed to pdf each time it is called. For an explanation of the other
arguments, see IMSLS_USER_PDF.
IMSLS_PREDICTED_CLASS_PROB,
float **pred_class_prob,
(Output)
The address of a pointer to an array of size n_patterns by n_classes, where n_classes is the
number of target classifications. The values in the i-th row are
the predicted classification
probabilities associated with the target classes. pred_class_prob[i*n_classes+j]
is the estimated probability that the i-th pattern belongs to the
j-th target classes.
IMSLS_PREDICTED_CLASS_PROB_USER,
float pred_class_prob[], (Output)
Storage for array pred_class_prob is
provided by the user. See IMSLS_PREDICTED_CLASS_PROB
for a description.
IMSLS_RETURN_USER,
int classification[]
(Output)
An array of length n_patterns containing
the predicted classifications for each pattern described by the input attributes
in nominal and
continuous.
Description
Function imsls_f_naive_bayes_classification estimates classification probabilities from a previously trained Naive Bayes classifier. Two arrays are used to describe the values of the nominal and continuous attributes used for calculating these probabilities. The predicted classification returned by this function is the class with the largest estimated classification probability. The classification probability estimates for each pattern can be obtained using the optional argument IMSLS_PREDICTED_CLASS_PROB.
Examples
Example 1
Fisher’s (1936) Iris data is often used for benchmarking classification algorithms. It is one of the IMSL data sets and consists of the following continuous input attributes and classification target:
Continuous Attributes: X0(sepal length), X1(sepal width), X2(petal length), and X3(petal width)
Classification (Iris Type): Setosa, Versicolour or Virginica.
This example trains a Naive Bayes classifier using 150 training patterns from Fisher’s data then classifies ten unknown plants using their sepal and petal measurements.
#include <imsls.h>
#include <stdio.h>
int main(){
int i, j;
int n_patterns =150; /* 150 training patterns */
int n_continuous =4; /* four continuous input attributes */
int n_classes =3; /* three classification categories */
int classification[150], *classErrors, *predictedClass;
float *pred_class_prob, continuous[150*4] ;
float *irisData; /* Fishers Iris Data */
char *classLabel[] = {"Setosa ", "Versicolour", "Virginica "};
char dashes[] = {
"--------------------------------------------------------------"};
Imsls_f_nb_classifier *nb_classifier;
/* irisData[]: The raw data matrix. This is a 2-D matrix with 150
/* rows and 5 columns. The last 4 columns are the
/* continuous input attributes and the 1st column is
/* the classification category (1-3). These data
/* contain no categorical input attributes. */
irisData = imsls_f_data_sets(3,0);
/* Data corrections described in the KDD data mining archive */
irisData[5*34+4] = 0.1;
irisData[5*37+2] = 3.1;
irisData[5*37+3] = 1.5;
/* setup the required input arrays from the data matrix */
for(i=0; i<n_patterns; i++){
classification[i] = (int) irisData[i*5]-1;
for(j=1; j<=n_continuous; j++) {
continuous[i*n_continuous+j-1] = irisData[i*5+j];
}
}
classErrors = imsls_f_naive_bayes_trainer(
n_patterns, n_classes, classification,
IMSLS_CONTINUOUS, n_continuous, continuous,
IMSLS_NB_CLASSIFIER, &nb_classifier, 0);
printf(" Iris Classification Error Rates\n");
printf("%s\n",dashes);
printf(" Setosa Versicolour Virginica | TOTAL\n");
printf(" %d/%d %d/%d %d/%d | %d/%d\n",
classErrors[0], classErrors[1],
classErrors[2], classErrors[3], classErrors[4],
classErrors[5], classErrors[6], classErrors[7]);
printf("%s\n\n", dashes);
/* CALL NAIVE_BAYES_CLASSIFICATION *************************** */
predictedClass = imsls_f_naive_bayes_classification(
nb_classifier, n_patterns,
IMSLS_CONTINUOUS, continuous,
IMSLS_PREDICTED_CLASS_PROB,
&pred_class_prob, 0);
printf(" PROBABILITIES FOR INCORRECT CLASSIFICATIONS\n",dashes);
printf("\nTRAINING PATTERNS| PREDICTED\t|\n");
printf(" X1 X2 X3 X4 | CLASS\t| CLASS\tP(0) P(1) P(2)|\n");
printf("%s|\n", dashes);
for(i=0; i<n_patterns; i++){
if(classification[i] == predictedClass[i]) continue;
printf(" %4.1f%4.1f%4.1f%4.1f| %s\t| %s\t%4.2f %4.2f %4.2f|\n",
continuous[i*n_continuous], continuous[i*n_continuous+1],
continuous[i*n_continuous+2], continuous[i*n_continuous+3],
classLabel[classification[i]], classLabel[predictedClass[i]],
pred_class_prob[i*n_classes], pred_class_prob[i*n_classes+1],
pred_class_prob[i*n_classes+2]);
}
printf("%s|\n", dashes);
imsls_f_nb_classifier_free(nb_classifier);
}
Output
For Fisher’s data, the Naive Bayes classifier incorrectly classified 6 of the 150 training patterns.
Iris Classification Error Rates
--------------------------------------------------------------
Setosa Versicolour Virginica | TOTAL
0/50 3/50 3/50 | 6/150
--------------------------------------------------------------
PROBABILITIES FOR INCORRECT CLASSIFICATIONS
TRAINING PATTERNS| PREDICTED |
X1 X2 X3 X4 | CLASS | CLASS P(0) P(1) P(2)|
--------------------------------------------------------------|
6.9 3.1 4.9 1.5| Versicolour | Virginica 0.00 0.46 0.54|
5.9 3.2 4.8 1.8| Versicolour | Virginica 0.00 0.16 0.84|
6.7 3.0 5.0 1.7| Versicolour | Virginica 0.00 0.08 0.92|
4.9 2.5 4.5 1.7| Virginica | Versicolour 0.00 0.97 0.03|
6.0 2.2 5.0 1.5| Virginica | Versicolour 0.00 0.96 0.04|
6.3 2.8 5.1 1.5| Virginica | Versicolour 0.00 0.71 0.29|
--------------------------------------------------------------|
Example 2
This example uses the spam benchmark data available from the Knowledge Discovery Databases archive maintained at the University of California, Irvine: http://archive.ics.uci.edu/ml/datasets/Spambase.
These data contain of 4601 patterns consisting of 57 continuous attributes and one classification. 41% of these patterns are classified as spam and the remaining as non-spam. The first 54 continuous attributes are word or symbol percentages. That is, they are percents scaled from 0 to 100% representing the percentage of words or characters in the email that contain a particular word or character. The last three continuous attributes are word lengths. For a detailed description of these data visit the KDD archive at the above link.
In this example, percentages are transformed using the
arcsin/square root transformation 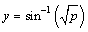 . The last three attributes, word
lengths, are transformed using square roots. Transformed percentages and
the first word length attribute are modeled using the Gaussian
distribution. The last two word lengths are modeled using the log normal
distribution.
. The last three attributes, word
lengths, are transformed using square roots. Transformed percentages and
the first word length attribute are modeled using the Gaussian
distribution. The last two word lengths are modeled using the log normal
distribution.
#include <imsls.h>
#include <stdlib.h>
#include <stdio.h>
static void printErrorRates(int classification_errors[6],
int n, char *label);
int main(){
int i, j, k;
int condPdfTableLength = 0;
int n_patterns;
int n_variables;
int n_sample = 2000;
int n_classes = 2; /* spam or no spam */
int n_continuous = 57;
int *classErrors = NULL;
int *classification = NULL;
int classSample[2000];
int *predictedClass = NULL;
int *rndSampleIndex = NULL;
int classification_errors[6];
float *continuous, *continuousSample;
char* label1 =
" Trainer from Training Dataset of %d Observations \n";
char* label2 =
" Classifier for Entire Dataset of %d Observations \n";
Imsls_f_nb_classifier *nb_classifier=NULL;
float *spamData;
int n_spam = 0;
spamData = imsls_f_data_sets(11, IMSLS_N_OBSERVATIONS, &n_patterns,
IMSLS_N_VARIABLES, &n_variables, 0);
continuous =
(float*)malloc((n_patterns*n_continuous)*sizeof(float));
continuousSample =
(float*)malloc((n_sample*n_continuous)*sizeof(float));
classification = (int*)malloc(n_patterns*sizeof(int));
/* map continuous attributes into transformed representation */
for(i=0; i<n_patterns; i++){
for(j=0; j<n_continuous; j++) {
if (j < 54 ) {
continuous[i*(n_variables-1)+j] = (float)
asin(sqrt( spamData[i*n_variables+j]/100));
} else {
continuous[i*(n_variables-1)+j] =
spamData[i*n_variables+j];
}
}
classification[i] = (int)spamData[(i*n_variables)+n_variables-1];
if(classification[i] == 1) n_spam++;
}
printf("Number of Patterns = %d Number Classified as Spam = %d \n\n",
n_patterns, n_spam);
/* select random sample for training Naive Bayes Classifier */
imsls_random_seed_set(1234567);
rndSampleIndex=imsls_random_sample_indices(n_sample, n_patterns, 0);
for(k=0; k<n_sample; k++){
i = rndSampleIndex[k]-1;
classSample[k] = classification[i];
for(j=0; j<n_continuous; j++) {
continuousSample[k*n_continuous+j] =
continuous[i*n_continuous+j];
}
}
/* Train Naive Bayes Classifier */
classErrors = imsls_f_naive_bayes_trainer(n_sample, n_classes,
classSample,
IMSLS_CONTINUOUS, n_continuous, continuousSample,
IMSLS_NB_CLASSIFIER, &nb_classifier, 0);
/* print error rates for training sample */
printErrorRates(classErrors, n_sample, label1);
/* CALL NAIVE_BAYES_CLASSIFICATION TO CLASSIFIY ENTIRE DATASET */
predictedClass = imsls_f_naive_bayes_classification(nb_classifier,
n_patterns,
IMSLS_CONTINUOUS, continuous, 0);
/* calculate classification error rates for entire dataset */
for(i=0; i<6; i++) classification_errors[i] = 0;
for(i=0; i<n_patterns; i++){
switch (classification[i])
{
case 0:
classification_errors[1]++;
if(classification[i] != predictedClass[i])
classification_errors[0]++;
break;
case 1:
classification_errors[3]++;
if(classification[i] != predictedClass[i])
classification_errors[2]++;
break;
}
classification_errors[5] =
classification_errors[1]+classification_errors[3];
classification_errors[4] =
classification_errors[0]+classification_errors[2];
}
/* print error rates for entire dataset */
printErrorRates(classification_errors, n_patterns, label2);
}
static void printErrorRates(int classification_errors[6],
int n, char *label)
{
double p, p1, p0;
p0 = 100.0*classification_errors[0]/classification_errors[1];
p1 = 100.0*classification_errors[2]/classification_errors[3];
p = 100.0*classification_errors[4]/classification_errors[5];
printf(" Classification Error Rates Reported by\n");
printf(label, n);
printf("----------------------------------------------------\n");
printf(" Not Spam Spam | TOTAL\n");
printf(" %d/%d=%4.1f%% %d/%d=%4.1f%% | %d/%d=%4.1f%%\n",
classification_errors[0], classification_errors[1],
p0, classification_errors[2], classification_errors[3],
p1, classification_errors[4], classification_errors[5], p);
printf("----------------------------------------------------\n\n");
return;
}
Output
It is interesting to note that the classification error rates obtained by training a classifier from a random sample is slightly lower than those obtained from training a classifier with all 4601 patterns. When the classifier is trained using all 4601 patterns, the overall classification error rate was 12.9% (see Example 3 for imsls_f_naive_bayes_trainer). It is 12.4% for a random sample of 2000 patterns.
Number of Patterns = 4601 Number Classified as Spam = 1813
Classification Error Rates Reported by
Trainer from Training Dataset of 2000 Observations
----------------------------------------------------
Not Spam Spam | TOTAL
31/1202= 2.6% 218/798=27.3% | 249/2000=12.4%
----------------------------------------------------
Classification Error Rates Reported by
Classifier for Entire Dataset of 4601 Observations
----------------------------------------------------
Not Spam Spam | TOTAL
81/2788= 2.9% 549/1813=30.3% | 630/4601=13.7%
----------------------------------------------------
