Trains a Naive Bayes classifier.
Synopsis
#include <imsls.h>
int *imsls_f_naive_bayes_trainer (int n_patterns, int n_classes, int classification[], ..., 0)
The type double function is imsls_d_naive_bayes_trainer.
Required Arguments
int n_patterns
(Input)
Number of training patterns.
int n_classes
(Input)
Number of target classifications.
int classification[]
(Input)
Array of size n_patterns containing
the target classifications for the training patterns. These must be
encoded from zero to n_classes-1. Any
value outside this range is considered a missing value. In this case, the
data in that pattern are not used to train the Naive Bayes classifier.
However, any pattern with missing values is still classified after the
classifier is trained.
Return Value
An array of size (n_classes+1) by 2 containing the number of classification errors and the number of non-missing classifications for each target classification plus the overall totals for these errors. For i < n_classes, the i-th row contains the number of classification errors for the i-th class and the number of patterns with non-missing classifications for that class. The last row contains the number of classification errors totaled over all target classifications and the total number of patterns with non-missing target classifications. The memory allocated for this array can be released using imsls_free.
If training is unsuccessful, NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
int
*imsls_f_naive_bayes_trainer (int
n_patterns,
int n_classes,
int classification[],
IMSLS_CONTINUOUS, int
n_continuous,
float continuous[],
IMSLS_NOMINAL, int n_nominal, int n_categories[], int nominal[],
IMSLS_PRINT_LEVEL, int print_level,
IMSLS_IGNORE_MISSING_VALUE_PATTERNS,
IMSLS_DISCRETE_SMOOTHING_PARM, float
d_lambda,
IMSLS_CONTINUOUS_SMOOTHING_PARM, float
c_lambda,
IMSLS_ZERO_CORRECTION, float
zero_correction,
IMSLS_SELECTED_PDF, int selected_pdf[],
IMSLS_GAUSSIAN_PDF, float
means[], float
stdev[],
IMSLS_LOG_NORMAL_PDF,
float
logMean[], float
logStdev[],
IMSLS_GAMMA_PDF, float
a[], float
b[],
IMSLS_POISSON_PDF, float
theta[],
IMSLS_USER_PDF, float
pdf(),
IMSLS_USER_PDF_WITH_PARMS, float
pdf(), void
*parms,
IMSLS_STATISTICS, float
**means, float
**stdev,
IMSLS_STATISTICS_USER, float
means[], float
stdev[],
IMSLS_PREDICTED_CLASS, int **predicted_class,
IMSLS_PREDICTED_CLASS_USER, int predicted_class[],
IMSLS_PREDICTED_CLASS_PROB, float
**pred_class_prob,
IMSLS_PREDICTED_CLASS_PROB_USER, float
pred_class_prob[],
IMSLS_CLASS_ERROR, float
**class_error,
IMSLS_CLASS_ERROR_USER, float class_error[],
IMSLS_COUNT_TABLE, int **count_table,
IMSLS_COUNT_TABLE_USER, int count_table[],
IMSLS_NB_CLASSIFIER, Imsls_f_nb_classifier **nb_classifier,
IMSLS_RETURN_USER, int
classErrors[],
0)
Optional Arguments
IMSLS_CONTINUOUS, int n_continuous, float continuous[] (Input)
n_continuous is the
number of continuous attributes and continuous is an array
of size n_patterns by n_continuous
containing the training values for the continuous attributes. The
i-th row contains the input attributes for the i-th training
pattern. The j-th column of
continuous
contains the values for the j-th continuous
attribute. Missing values should be set equal to imsls_f_machine(6)=NaN.
Patterns with both non-missing and missing values are used to
train the classifier unless the IMSLS_IGNORE_MISSING_VALUE_PATTERNS
argument is supplied. If the IMSLS_CONTINUOUS argument is not supplied, n_continuous is
assumed equal to zero.
IMSLS_NOMINAL,
int n_nominal, int
n_categories[],
int nominal[]
(Input)
n_nominal is the
number of nominal attributes. n_categories is an
array of length n_nominal containing
the number of categories associated with each nominal attribute. These
must all be greater than zero. nominal is an array of size n_patterns by n_nominal containing
the training values for the nominal attributes. The i-th row contains
the nominal input attributes for the i-th
pattern. The j-th column of
this matrix contains the classifications for the j-th nominal
attribute. The values for the j-th nominal
attribute are expected to be encoded with integers starting from 0 to n_categories[i]-1.
Any value outside this range is treated as a missing value. Patterns with both
non-missing and missing values are used to train the classifier unless the IMSLS_IGNORE_MISSING_VALUE_PATTERNS
option is supplied. If the IMSLS_NOMINAL argument
is not supplied, n_nominal is assumed
equal to zero.
IMSLS_PRINT_LEVEL,
int
print_level (Input)
Print levels for printing data warnings and final
results. print_level should be
set to ne of the following values:
|
print_level |
Description |
|
IMSLS_NONE |
Printing of data warnings and final results is suppressed. |
|
IMSLS_FINAL |
Prints final summary of Naive Bayes classifier training. |
|
IMSLS_DATA_WARNINGS |
Prints information about missing values and PDF calculations equal to zero. |
|
IMSLS_TRACE_ALL |
Prints final summary plus all data warnings associated with missing values and PDF calculations equal to zero. |
Default: IMSLS_NONE.
IMSLS_IGNORE_MISSING_VALUE_PATTERNS
(Input)
By default, patterns with both missing and non-missing values
are used to train the classifier. This option causes the algorithm to
ignore patterns with one or more missing input attributes during training.
However, classification predictions are still returned for all patterns.
IMSLS_DISCRETE_SMOOTHING_PARM, float d_lambda
(Input)
Parameter for calculating smoothed estimates of conditional
probabilities for discrete attributes. This parameter must be
non-negative.
Default: Laplace smoothing of conditional probabilities,
i.e. d_lambda=1.
IMSLS_CONTINUOUS_SMOOTHING_PARM, float c_lambda
(Input)
Parameter for calculating smoothed estimates of conditional
probabilities for continuous attributes. This parameter must be
non-negative.
Default: No smoothing of conditional probabilities for
continuous attributes, i.e. c_lambda=0.
IMSLS_ZERO_CORRECTION,
float
zero_correction (Input)
Parameter used to replace conditional
probabilities equal to zero numerically. This parameter must be
non-negative.
Default: No correction, i.e. zero_correction =
0.
IMSLS_SELECTED_PDF, int
selected_pdf[] (Input)
An array
of length n_continuous
specifying the distribution for each continuous input attribute. If
this argument is not supplied, conditional probabilities for all continuous
attributes are calculated using the Gaussian probability density function
with its parameters estimated from the training patterns, i.e. selected_pdf[i] = IMSLS_GAUSSIAN.
This argument allows users to select other distributions using the following
encoding:
|
selected_pdf[i] |
Probability Density Function |
|
IMSLS_GAUSSIAN |
Gaussian (See IMSLS_GAUSSIAN_PDF). |
|
IMSLS_LOG_NORMAL |
Log-normal (See IMSLS_LOG_NORMAL_PDF). |
|
IMSLS_GAMMA |
Gamma (See IMSLS_GAMMA_PDF). |
|
IMSLS_POISSON |
Poisson (See IMSLS_POISSON_PDF). |
|
IMSLS_USER |
User Defined (See IMSLS_USER_PDF). |
selected_pdf[i], specifies the probability density function for the i-th continuous input attribute.
IMSLS_GAUSSIAN_PDF, float
means[], float
stdev[] (Input)
The means and stdev are two arrays
each of size n_gauss by n_classes where n_gauss represents the
number of Gaussian attributes as specified by optional argument IMSLS_SELECTED_PDF
(i.e., the number of elements in selected_pdf equal to
IMSLS_GAUSSIAN). The
i-th row of means and stdev contains the
means and standard deviations respectively for the i-th Gaussian
attribute in continuous for each
value of the target classification. means[i*n_classes+j]
is used as the mean for the i-th Gaussian attribute when the target
classification equals j, and stdev[i*n_classes+j]
is used as the standard deviation for the i-th Gaussian attribute when
the target classification equals j. This argument
is ignored if n_continuous =
0.
Default: The means and standard deviations for all Gaussian attributes are
estimated from the means and standard deviations of the the training patterns.
These estimates are the traditional BLUE (Best Linear Unbiased Estimates) for
the parameters of a Gaussian distribution.
IMSLS_LOG_NORMAL_PDF, float
logMean[], float
logStdev[] (Input)
Two arrays
each of size n_logNormal by n_classes where n_logNormal represents
the number of log-normal attributes as specified by optional argument IMSLS_SELECTED_PDF
(i.e., the number of elements in selected_pdf equal to
IMSLS_LOG_NORMAL).
The i-th row of logMean and logStdev contains the
means and standard deviations respectively for the i-th log-normal attribute for each value of the
target classification.
logMean[i*n_classes+j]
is used as the mean for the i-th log-normal attribute when the target
classification equals j, and logStdev[i*n_classes+j]
is used as the standard deviation for the i-th log-normal attribute when
the target classification equals j. This argument
is ignored if n_continuous =
0.
Default: The means and standard deviations for all log-normal
attributes are estimated from the means and standard deviations of the the
training patterns. These estimates are the traditional MLE (Maximum Likelihood
Estimates) for the parameters of a log-normal distribution.
IMSLS_GAMMA_PDF, float
a[], float
b[] (Input)
Two arrays
each of size n_gamma by n_classes containing
the means and standard deviations for the Gamma continuous
attributes, where n_gamma represents the
number of gamma distributed continuous variables as specified by the optional
argument IMSLS_SELECTED_PDF
(i.e. the number of elements in selected_pdf equal to
IMSLS_GAMMA). The i-th row of a and b contains the shape
and scale parameters for the i-th Gamma attribute for each value of the
target classification. a[i*n_classes+j] is
used as the shape parameter for the i-th Gamma attribute when the target
classification equals j, and
b[i*n_classes+j]
is used as the scale parameter for the i-th Gamma attribute when the
target classification equals j. This argument
is ignored if n_continuous = 0.
Default: The shape and scale parameters for all Gamma attributes are
estimated from the training patterns. These estimates are the traditional MLE
(Maximum Likelihood Estimates) for the parameters of a Gamma distribution.
IMSLS_POISSON_PDF, float
theta[] (Input)
An array
of size n_poisson by n_classes containing
the means for the Poisson attributes, where n_poisson represents
the number of Poisson distributed continuous variables as specified by the
optional argument IMSLS_SELECTED_PDF
(i.e. the number of elements in selected_pdf equal to
IMSLS_POISSON).The
i-th row of theta contains the
means for the i-th Poisson attribute for each value of the target
classification. theta[i*n_classes+j]
is used as the mean for the i-th Poisson attribute
when the target classification equals j. This argument
is ignored if n_continuous= 0.
Default: The means (theta) for all Poisson
attributes are estimated from the means of the the training patterns. These
estimates are the traditional MLE (Maximum Likelihood Estimates) for the
parameters of a Poisson distribution.
IMSLS_USER_PDF,
float pdf(int index[],
float
x)
(Input)
The user-supplied probability density function and
parameters used to calculate the conditional probability density for continuous
input attributes is required when selected_pdf[i]= IMSLS_USER.
When pdf is called, x will equal continuous[i*n_continuous+j],
and index is an
array of length 3 which will contain the following values for i,
j, and k:
|
index |
Value |
|
i = pattern index | |
|
index[1] |
j = attribute index |
|
index[2] |
k = target classification |
The pattern index
ranges from 0 to n_patterns-1 and
identifies the pattern index for x. The
attributes index ranges from 0 to n_categories[i]-1, and
k=classification[i].
This
argument is ignored if n_continuous = 0. By default the
Gaussian PDF is used for calculating the conditional probability densities using
either the means and variances calculated from the training patterns or those
supplied in IMSLS_GAUSSIAN_PDF.
On
some platforms, imsls_f_naive_bayes_trainer
can evaluate the user-supplied function pdf in parallel. This
is done only if the function imsls_omp_options
is called to flag user-defined functions as thread-safe. A function is
thread-safe if there are no dependencies between calls. Such dependencies are
usually the result of writing to global or static variables.
IMSLS_USER_PDF_WITH_PARMS, float
pdf(int index[], float x, void *parms),
void *parms, (Input)
The user-supplied probability density
function and parameters used to calculate the conditional probability density
for continuous input attributes is required when selected_pdf[i]= IMSLS_USER.
PDF also accepts
a pointer to parms supplied by the user. The parameters pointed to by
parms are passed to pdf each time it is called. For an
explanation of the other arguments, see IMSLS_USER_PDF.
IMSLS_STATISTICS,
float **means, float
**stdev (Output)
The
address of pointers to two arrays of size n_continuous by n_classes containing
the means and standard deviations for the continuous attributes segmented by the
target classes. The structure of these matrices is identical to the
structure described for the IMSLS_GAUSSIAN_PDF
argument. The i-th row of means and stdev contains the means
and standard deviations respectively of the i-th continuous attribute for
each value of the target classification. That is, means[i*n_classes+j]
is the mean for the i-th continuous attribute when the target
classification equals j, and stdev[i*n_classes+j]
is the standard deviation for the i-th continuous attribute when the
target classification equals j, unless there are no training patterns for
this condition. If there are no training patterns in the i, j-th
cell then the mean and standard deviation for that cell is computed using the
mean and standard deviation for the i-th continuous attribute calculated
using all of its non-missing values. Standard deviations are estimated
using the minimum variance unbiased estimator.
IMSLS_STATISTICS_USER, float
means[], float
stdev[] (Output)
Storage
for matrices means and stdev provided
by the user. See IMSLS_STATISTICS.
IMSLS_PREDICTED_CLASS, int **pred_class (Output)
The
address of a pointer to an array of size n_patterns containing
the predicted classification for each training pattern.
IMSLS_PREDICTED_CLASS_USER,
int pred_class[]
(Output)
Storage for array pred_class provided by the user. See IMSLS_PREDICTED_CLASS.
IMSLS_PREDICTED_CLASS_PROB, float **pred_class_prob (Output)
The
address of a pointer to an array of size n_patterns by n_classes. The
values in the i-th row are the predicted classification probabilities
associated with the target classes. pred_class_prob[i*n_classes+j]
is the estimated probability that the
i-th pattern belongs to the
j-th target class.
IMSLS_PREDICTED_CLASS_PROB_USER,
float pred_class_prob[]
(Output)
Storage for array pred_class_prob is provided by the user.
See IMSLS_PREDICTED_CLASS_PROB
for a description.
IMSLS_CLASS_ERROR, float **class_error (Output)
The
address of a pointer to an array with n_patterns containing
the classification probability errors for each pattern in the training
data. The classification error for the i-th training
pattern is equal to 1- pred_class_prob[i*n_classes+k] where
k=classification[i].
IMSLS_CLASS_ERROR_USER
float class_error[] (Output)
Storage
for array class_error is
provided by the user. See IMSLS_CLASS_ERROR for
a description.
IMSLS_COUNT_TABLE int
**count_table (Output)
The
address of a pointer to an array of size
 ,
,
where m = n_nominal -1.
count_table[i*n_nominal*n_classes+j*n_classes+k] is equal to the
number of training patterns for the i-th nominal attribute, when the
classification[i]=j and nominal[i*n_classes+j]=k.
IMSLS_COUNT_TABLE_USER
int count_table[]
(Output)
Storage for matrix count_table provided by the user. See IMSLS_COUNT_TABLE.
IMSLS_NB_CLASSIFIER
Imsls_f_nb_classifier **nb_classifier (Output)
The
address of a pointer to an Imsls_f_nb_classifier structure. Upon
return, the structure is populated with the trained Naive Bayes
classifier. This is required input to imsls_f_naive_bayes_classification.
Memory allocated to this structure is released using imsls_f_nb_classifier_free.
IMSLS_RETURN_USER,
int classErrors[] (Output)
An
array of size (n_classes +1) by 2
containing the number of classification errors and the number of non-missing
classifications for each target classification and the overall totals. For
0 ≤ i < n_classes, the
i-th row contains the number of classification errors for the i-th
class and the number of patterns with non-missing classifications for that
class. The last row contains the number of classification errors totaled over
all target classifications and the total number of patterns with non-missing
target classifications.
Description
Function imsls_f_naive_bayes_trainer trains a Naive Bayes classifier for classifying data into one of n_classes target classes. Input attributes can be a combination of both nominal and continuous data. Ordinal data can be treated as either nominal attributes or continuous. If the distribution of the ordinal data is known or can be approximated using one of the continuous distributions, then associating them with continuous attributes allows a user to specify that distribution. Missing values are allowed.
Let C be the classification attribute with target categories 0, 1, …, n_classes-1, and let XT={x1, x2, …, xk} be a vector valued array of k = n_nominal+n_continuous input attributes. The classification problem simplifies to estimate the conditional probability P(C|X) from a set of training patterns. The Bayes rule states that this probability can be expressed as the ratio:
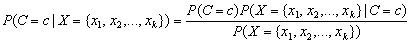 ,
,
where c is equal to one of the target classes
0, 1, …, n_classes-1. In
practice, the denominator of this expression is constant across all target
classes since it is only a function of the given values of X. As a
result, the Naive Bayes algorithm does not expend computational time estimating
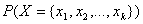 for every pattern. Instead,
a Naive Bayes classifier calculates the numerator
for every pattern. Instead,
a Naive Bayes classifier calculates the numerator 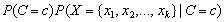 for each target class and then
classifies X to the target class with the largest value, i.e.,
for each target class and then
classifies X to the target class with the largest value, i.e.,
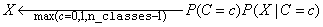 .
.
The classifier simplifies this calculation by assuming conditional independence. That is it assumes that:
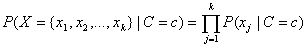 .
.
This is equivalent to assuming that the values of the input attributes, given C, are independent of one another, i.e.,
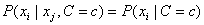 , for all
i≠j.
, for all
i≠j.
In real world data this assumption rarely holds, yet in
many cases this approach results in surprisingly low classification error rates.
Thus, the estimate of 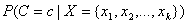 from a Naive Bayes classifier
is generally an approximation. Classifying patterns based upon the Naive Bayes
algorithm can have acceptably low classification error rates.
from a Naive Bayes classifier
is generally an approximation. Classifying patterns based upon the Naive Bayes
algorithm can have acceptably low classification error rates.
For nominal attributes, this implementation of the Naive Bayes classifier estimates conditional probabilities using a smoothed estimate:
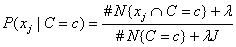 ,
,
where #N{Z}is the number of training patterns with attribute Z and j is equal to the number of categories associated with the j-th nominal attribute.
The probability 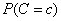 is also estimated using a
smoothed estimate:
is also estimated using a
smoothed estimate:
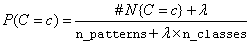
These estimates correspond to the maximum a priori (MAP) estimates for a Dirichelet prior assuming equal priors. The smoothing parameter can be any non-negative value. Setting λ = 0 corresponds to no smoothing. The default smoothing used in this algorithm, λ = 1, is commonly referred to as Laplace smoothing. This can be changed using the optional argument IMSLS_DISCRETE_SMOOTHING_PARM.
For continuous attributes, the same conditional probability
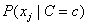 in the Naive Bayes formula is replaced
with the conditional probability density function
in the Naive Bayes formula is replaced
with the conditional probability density function 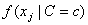 . By default, the density
function for continuous attributes is the Gaussian density function:
. By default, the density
function for continuous attributes is the Gaussian density function:
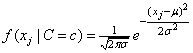 ,
,
where μ and σ
are the conditional mean and variance, i.e. the mean and variance of
xj when 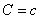 . By default the conditional mean
and standard deviations are estimated using the sample mean and standard
deviation of the training patterns. These are returned in the optional
argument IMSLS_STATISTICS.
. By default the conditional mean
and standard deviations are estimated using the sample mean and standard
deviation of the training patterns. These are returned in the optional
argument IMSLS_STATISTICS.
In addition to the default IMSLS_GAUSSIAN, users can select three other continuous distributions to model the continuous attributes using the argument IMSLS_SELECTED_PDF. These are the Log Normal, Gamma, and Poisson distributions selected by setting the entries in selected_pdf to IMSLS_LOG_NORMAL, IMSLS_GAMMA or IMSLS_POISSON. Their probability density functions are equal to:
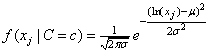 ,
,
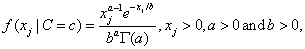
and
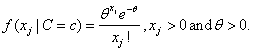
By default parameters for these distributions are estimated from the training patterns using the maximum likelihood method. However, they can also be supplied using the optional input arguments IMSLS_GAUSSIAN_PDF, IMSLS_LOG_NORMAL_PDF, IMSLS_GAMMA_PDF and IMSLS_POISSON_PDF.
The default Gaussian PDF can be changed and each continuous attribute can be assigned a different density function using the argument IMSLS_SELECTED_PDF. If any entry in selected_pdf is equal to IMSLS_USER, the user must supply their own PDF calculation using the IMSLS_USER_PDF argument. Each continuous attribute can be modeled using a different distribution if appropriate.
Smoothing conditional probability calculations for continuous attributes is controlled by the IMSLS_CONTINOUS_SMOOTHING_PARM and IMSLS_ZERO_CORRECTION optional arguments. By default conditional probability calculations for continuous attributes are unadjusted for calculations near zero. If the value of c_lambda is set using the IMSLS_CONTINOUS_SMOOTHING_PARM argument, the algorithm adds c_lambda to each continuous probability calculation. This is similar to the effect of d_lambda for the corresponding discrete calculations. By default c_lambda=0.
The value of zero_correction
from the IMSLS_ZERO_CORRECTION
argument is used when 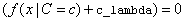 . If this condition occurs, the
conditional probability is replaced with the value of zero_correction.
By default zero_correction
=
0.
. If this condition occurs, the
conditional probability is replaced with the value of zero_correction.
By default zero_correction
=
0.
Examples
Example 1
Fisher’s (1936) Iris data is often used for benchmarking classification algorithms. It is one of the IMSL data sets and consists of the following continuous input attributes and classification target:
Continuous Attributes: X0(sepal length), X1(sepal width), X2(petal length), and X3(petal width)
Classification (Iris Type): Setosa, Versicolour, or Virginica.
This example trains a Naive Bayes classifier using 150 training patterns with these data.
#include <imsls.h>
#include <stdio.h>
int main(){
int i, j;
int n_patterns =150; /* 150 training patterns */
int n_continuous =4; /* four continuous input attributes */
int n_classes =3; /* three classification categories */
int classification[150], *classErrors, *predictedClass;
float *pred_class_prob, continuous[4*150] ;
float *irisData; /* Fishers Iris Data */
char *classLabel[3] = {"Setosa ", "Versicolour", "Virginica "};
Imsls_f_nb_classifier *nb_classifier;
imsls_omp_options(IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
/* irisData[]: The raw data matrix. This is a 2-D matrix
with 150 rows and 5 columns. The last 4 columns are the
continuous input attributes and the 1st column is the
classification category (1-3). These data contain no */
/* nominal input attributes. */
irisData = imsls_f_data_sets(3,0);
/* Data corrections described in the KDD data mining archive */
irisData[5*34+4] = 0.1;
irisData[5*37+2] = 3.1;
irisData[5*37+3] = 1.5;
/* setup the required input arrays from the data matrix */
for(i=0; i<n_patterns; i++){
classification[i] = (int) irisData[i*5]-1;
for(j=1; j<=n_continuous; j++)
continuous[i*n_continuous+j-1] = irisData[i*5+j];
}
classErrors = imsls_f_naive_bayes_trainer(n_patterns,
n_classes, classification,
IMSLS_CONTINUOUS, n_continuous, continuous,
IMSLS_NB_CLASSIFIER, &nb_classifier, 0);
printf(" Iris Classification Error Rates\n");
printf("----------------------------------------------\n");
printf(" Setosa Versicolour Virginica | TOTAL\n");
printf(" %d/%d %d/%d %d/%d | %d/%d\n",
classErrors[0], classErrors[1],
classErrors[2], classErrors[3],
classErrors[4], classErrors[5],
classErrors[6], classErrors[7]);
printf("----------------------------------------------\n\n");
};
Output
For Fisher’s data, the Naive Bayes classifier incorrectly classified 6 of the 150 training patterns.
Iris Classification Error Rates
----------------------------------------------
Setosa Versicolour Virginica | TOTAL
0/50 3/50 3/50 | 6/150
----------------------------------------------
Example 2
This example trains a Naive Bayes classifier using 24 training patterns with four nominal input attributes. It illustrates the output available from the optional argument IMSLS_PRINT_LEVEL.
The first nominal attribute has three classifications and the others have three. The target classifications are contact lenses prescription: hard, soft or neither recommended. These data are benchmark data from the Knowledge Discovery Databases archive maintained at the University of California, Irvine: http://archive.ics.uci.edu/ml/datasets/Lenses.
#include <imsls.h>
#include <stdio.h>
int main(){
int inputData[5*24] = /* DATA MATRIX */
{ 1,1,1,1,3,1,1,1,2,2,1,1,2,1,3,1,1,2,2,1,1,2,1,1,3,1,2,1,
2,2,1,2,2,1,3,1,2,2,2,1,2,1,1,1,3,2,1,1,2,2,2,1,2,1,3,2,
1,2,2,1,2,2,1,1,3,2,2,1,2,2,2,2,2,1,3,2,2,2,2,3,3,1,1,1,
3,3,1,1,2,3,3,1,2,1,3,3,1,2,2,1,3,2,1,1,3,3,2,1,2,2,3,2,
2,1,3,3,2,2,2,3};
int i, j;
int n_patterns =24; / 24 training patterns */
int n_nominal =4; / 2 nominal input attributes */
int n_classes =3; / three classification categories */
int n_categories[4] = {3, 2, 2, 2};
int nominal[4*24], classification[24], *classErrors;
char *classLabel[3] = {"Hard ", "Soft ", "Neither"};
imsls_omp_options(IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
/* setup the required input arrays from the data
matrix */
/* subtract 1 from the data to ensure classes start at zero */
for(i=0; i<n_patterns; i++){
classification[i] = inputData[i*5+4]-1;
for(j=0; j<n_nominal; j++)
nominal[i*n_nominal+j]= inputData[i*5+j]-1;
}
classErrors = imsls_f_naive_bayes_trainer(n_patterns, n_classes,
classification,
IMSLS_NOMINAL, n_nominal, n_categories, nominal,
IMSLS_PRINT_LEVEL, IMSLS_FINAL, 0);
}
Output
For these data, only one of the 24 training patterns is
misclassified, pattern 17. The target classification for that pattern is 2
= “Neither”. However, since
P(class
=
2) = 0.3491
< P(class
= 1) =
0.5085,
pattern 17 is classified as class =
1, “Soft Contacts” recommended. The classification error for this
probability is calculated as
1.0 - 0.3491 = 0.6509.
--------UNCONDITIONAL TARGET CLASS PROBABILITIES---------
P(Class=0) = 0.1852 P(Class=1) = 0.2222 P(Class=2) = 0.5926
---------------------------------------------------------
----------------CONDITIONAL PROBABILITIES----------------
----------NOMINAL ATTRIBUTE 0 WITH 3 CATEGORIES----------
P(X(0)=0|Class=0)=0.4286 P(X(0)=1|Class=0)=0.2857 P(X(0)=2|Class=0)=0.2857
P(X(0)=0|Class=1)=0.3750 P(X(0)=1|Class=1)=0.3750 P(X(0)=2|Class=1)=0.2500
P(X(0)=0|Class=2)=0.2778 P(X(0)=1|Class=2)=0.3333 P(X(0)=2|Class=2)=0.3889
---------------------------------------------------------
----------NOMINAL ATTRIBUTE 1 WITH 2 CATEGORIES----------
P(X(1)=0|Class=0) = 0.6667 P(X(1)=1|Class=0) = 0.3333
P(X(1)=0|Class=1) = 0.4286 P(X(1)=1|Class=1) = 0.5714
P(X(1)=0|Class=2) = 0.4706 P(X(1)=1|Class=2) = 0.5294
---------------------------------------------------------
----------NOMINAL ATTRIBUTE 2 WITH 2 CATEGORIES----------
P(X(2)=0|Class=0) = 0.1667 P(X(2)=1|Class=0) = 0.8333
P(X(2)=0|Class=1) = 0.8571 P(X(2)=1|Class=1) = 0.1429
P(X(2)=0|Class=2) = 0.4706 P(X(2)=1|Class=2) = 0.5294
---------------------------------------------------------
----------NOMINAL ATTRIBUTE 3 WITH 2 CATEGORIES----------
P(X(3)=0|Class=0) = 0.1667 P(X(3)=1|Class=0) = 0.8333
P(X(3)=0|Class=1) = 0.1429 P(X(3)=1|Class=1) = 0.8571
P(X(3)=0|Class=2) = 0.7647 P(X(3)=1|Class=2) = 0.2353
---------------------------------------------------------
TRAINING PREDICTED CLASS
PATTERN P(class=0) P(class=1) P(class=2) CLASS CLASS ERROR
-----------------------------------------------------------------------
0 0.0436 0.1297 0.8267 2 2 0.1733
1 0.1743 0.6223 0.2034 1 1 0.3777
2 0.1863 0.0185 0.7952 2 2 0.2048
3 0.7238 0.0861 0.1901 0 0 0.2762
4 0.0194 0.1537 0.8269 2 2 0.1731
5 0.0761 0.7242 0.1997 1 1 0.2758
6 0.0920 0.0243 0.8836 2 2 0.1164
7 0.5240 0.1663 0.3096 0 0 0.4760
8 0.0253 0.1127 0.8621 2 2 0.1379
9 0.1182 0.6333 0.2484 1 1 0.3667
10 0.1132 0.0168 0.8699 2 2 0.1301
11 0.6056 0.1081 0.2863 0 0 0.3944
12 0.0111 0.1327 0.8562 2 2 0.1438
13 0.0500 0.7138 0.2362 1 1 0.2862
14 0.0535 0.0212 0.9252 2 2 0.0748
15 0.3937 0.1875 0.4188 2 2 0.5812
16 0.0228 0.0679 0.9092 2 2 0.0908
17 0.1424 0.5085 0.3491 2 1 0.6509
18 0.0994 0.0099 0.8907 2 2 0.1093
19 0.5986 0.0712 0.3301 0 0 0.4014
20 0.0101 0.0805 0.9093 2 2 0.0907
21 0.0624 0.5937 0.3439 1 1 0.4063
22 0.0467 0.0123 0.9410 2 2 0.0590
23 0.3909 0.1241 0.4850 2 2 0.5150
-----------------------------------------------------------------------
CLASSIFICATION ERRORS
Classification 0: 0/4
Classification 1: 0/5
Classification 2: 1/15
Total Errors: 1/24
Example 3
This example illustrates the power of Naive Bayes classification for text mining applications. This example uses the spam benchmark data available from the Knowledge Discovery Databases archive maintained at the University of California, Irvine: http://archive.ics.uci.edu/ml/datasets/Spambase and is one of the IMSL data sets.
These data consist of 4601 patterns consisting of 57 continuous attributes and one classification binary classification attribute. 41% of these patterns are classified as spam and the remaining as non-spam. The first 54 continuous attributes are word or symbol percentages. That is, they are percents scaled from 0 to 100% representing the percentage of words or characters in the email that contain a particular word or character. The last three continuous attributes are word lengths. For a detailed description of these data visit the KDD archive at the above link.
In this example, the program was written to evaluate
alternatives for modeling the continuous attributes. Since some are
percentages and others are lengths with widely different ranges, the
classification error rate can be influenced by scaling. Percentages are
transformed using the
arcsin/square root transformation 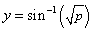 . This transformation often
produces a continuous attribute that is more closely approximated by a Gaussian
distribution. There are a variety of possible transformations for the word
length attributes. In this example, the square root transformation is
compared to a classifer with no transformation.
. This transformation often
produces a continuous attribute that is more closely approximated by a Gaussian
distribution. There are a variety of possible transformations for the word
length attributes. In this example, the square root transformation is
compared to a classifer with no transformation.
In addition, since this Naive Bayes algorithm allows users to select individual statistical distributions for modeling continuous attributes, the Gaussian and Log Normal distributions are investigated for modeling the continuous attributes.
#include <imsls.h>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
void print_error_rates(int classErrors[]);
int main(){
int i, j;
/* Inputs assuming all attributes, except family history,
are continuous */
int n_patterns; /* 4601 */
int n_variables; /* 57 + 1 classification */
int n_classes = 2; /* (spam or no spam) */
int n_continuous = 57;
int *classErrors = NULL;
int *classification = NULL;
int selected_pdf[57];
/* additional double variables */
float *continuous, *unscaledContinuous;
float *spamData;
int n_spam = 0;
static char *fmt = "%10.2f";
imsls_omp_options(IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
spamData = imsls_f_data_sets(11, IMSLS_N_OBSERVATIONS, &n_patterns,
IMSLS_N_VARIABLES, &n_variables, 0);
continuous = (float*) malloc( n_patterns * (n_variables-1)
* sizeof(float));
unscaledContinuous = (float*) malloc( n_patterns * (n_variables-1)
* sizeof(float));
classification = (int*) malloc( n_patterns*sizeof(int) );
for(i=0; i<n_patterns; i++){
for(j=0; j<(n_variables-1); j++) {
if (j<54) {
continuous[i*(n_variables-1)+j] = (float)
asin(sqrt( spamData[i*n_variables+j]/100));
} else {
continuous[i*(n_variables-1)+j] =
spamData[i*n_variables+j];
}
unscaledContinuous[i*(n_variables-1)+j] =
spamData[i*n_variables+j];
}
classification[i] = (int)spamData[(i*n_variables)+n_variables-1];
if(classification[i] == 1) n_spam++;
}
printf("Number of Patterns = %d \n", n_patterns);
printf(" Number Classified as Spam = %d \n\n", n_spam);
classErrors = imsls_f_naive_bayes_trainer(n_patterns, n_classes,
classification,
IMSLS_CONTINUOUS, n_continuous, unscaledContinuous, 0);
printf(" Unscaled Gaussian Classification Error Rates \n");
printf(" No Attribute Transformations \n");
printf(" All Attributes Modeled as Gaussian Variates.\n");
print_error_rates(classErrors);
imsls_free(classErrors);
classErrors = imsls_f_naive_bayes_trainer(n_patterns, n_classes,
classification, IMSLS_CONTINUOUS, n_continuous, continuous, 0);
printf(" Scaled Gaussian Classification Error Rates \n");
printf(" Arsin(sqrt) transformation of first 54 Vars. \n");
printf(" All Attributes Modeled as Gaussian Variates. \n");
print_error_rates(classErrors);
imsls_free(classErrors);
for(i=0; i<54; i++){
selected_pdf[i] = IMSLS_GAUSSIAN;
}
for(i=54; i<57; i++){
selected_pdf[i] = IMSLS_LOG_NORMAL;
}
classErrors = imsls_f_naive_bayes_trainer(n_patterns, n_classes,
classification,
IMSLS_CONTINUOUS, n_continuous, continuous,
IMSLS_SELECTED_PDF, selected_pdf, 0);
printf(" Gaussian/Log Normal Classification Error Rates \n");
printf(" Arsin(sqrt) transformation of 1st 54 Attributes. \n");
printf(" Gaussian - 1st 54 & Log Normal - last 3 Attributes\n");
print_error_rates(classErrors);
imsls_free(classErrors);
/* scale continuous attributes using z-score scaling */
for(i=0; i<n_patterns; i++){
for(j=54; j<57; j++) continuous[i*n_continuous+j] = (float)
sqrt(unscaledContinuous[i*n_continuous+j]);
}
for(i=0; i<57; i++){
selected_pdf[i] = IMSLS_GAUSSIAN;
}
classErrors = imsls_f_naive_bayes_trainer(n_patterns, n_classes,
classification,
IMSLS_CONTINUOUS, n_continuous, continuous,
IMSLS_SELECTED_PDF, selected_pdf, 0);
printf(" Scaled Classification Error Rates \n");
printf(" Arsin(sqrt) transformation of 1st 54 Attributes\n");
printf(" sqrt() transformation for last 3 Attributes \n");
printf(" All Attributes Modeled as Gaussian Variates. \n");
print_error_rates(classErrors);
imsls_free(classErrors);
for(i=54; i<57; i++){
selected_pdf[i] = IMSLS_LOG_NORMAL;
}
classErrors = imsls_f_naive_bayes_trainer(n_patterns, n_classes,
classification, IMSLS_CONTINUOUS, n_continuous, continuous,
IMSLS_SELECTED_PDF, selected_pdf, 0);
printf(" Scaled Classification Error Rates\n");
printf(" Arsin(sqrt) transformation of 1st 54 Attributes \n");
printf(" and sqrt() transformation for last 3 Attributes \n");
printf(" Gaussian - 1st 54 & Log Normal - last 3 Attributes\n");
print_error_rates(classErrors);
imsls_free(classErrors);
}
void print_error_rates(int classErrors[]){
float p0, p1, p2;
p0 = (float)100.0*classErrors[0]/classErrors[1];
p1 = (float)100.0*classErrors[2]/classErrors[3];
p2 = (float)100.0*classErrors[4]/classErrors[5];
printf("----------------------------------------------------\n");
printf(" Not Spam Spam | TOTAL\n");
printf(" %d/%d=%4.1f%% %d/%d=%4.1f%% | %d/%d=%4.1f%%\n",
classErrors[0], classErrors[1],
p0, classErrors[2], classErrors[3],
p1, classErrors[4], classErrors[5], p2);
printf("----------------------------------------------------\n\n");
}
Output
If the continuous attributes are left untransformed and modeled using the Gaussian distribution, the overall classification error rate is 18.4% with most of these occurring when spam is classified as “not spam.” The error rate for correctly classifying non-spam is 26.6%.
The lowest overall classification error rate occurs when the percentages are transformed using the arc-sin/square root transformation and the length attributes are untransformed using logs. Representing the transformed percentages as Gaussian attributes and the transformed lengths as log-normal attributes reduces the overall error rate to 14.2%. However, although the error rate for correctly classifying non-spam email is low for this case, the error rate for correctly classifying spam is high, about 28%.
In the end, the best model to identify spam may depend upon which type of error is more important, incorrectly classifying non-spam email or incorrectly classifying spam.
Data File Opened Successfully
Number of Patterns = 4601
Number Classified as Spam = 1813
Unscaled Gaussian Classification Error Rates
No Attribute Transformations
All Attributes Modeled as Gaussian Variates.
----------------------------------------------------
Not Spam Spam | TOTAL
743/2788=26.6% 102/1813= 5.6% | 845/4601=18.4%
----------------------------------------------------
Scaled Gaussian Classification Error Rates
Arsin(sqrt) transformation of first 54 Vars.
All Attributes Modeled as Gaussian Variates.
----------------------------------------------------
Not Spam Spam | TOTAL
84/2788= 3.0% 508/1813=28.0% | 592/4601=12.9%
----------------------------------------------------
Gaussian/Log Normal Classification Error Rates
Arsin(sqrt) transformation of 1st 54 Attributes.
Gaussian - 1st 54 & Log Normal - last 3 Attributes
----------------------------------------------------
Not Spam Spam | TOTAL
81/2788= 2.9% 519/1813=28.6% | 600/4601=13.0%
----------------------------------------------------
Scaled Classification Error Rates
Arsin(sqrt) transformation of 1st 54 Attributes
sqrt() transformation for last 3 Attributes
All Attributes Modeled as Gaussian Variates.
----------------------------------------------------
Not Spam Spam | TOTAL
74/2788= 2.7% 595/1813=32.8% | 669/4601=14.5%
----------------------------------------------------
Scaled Classification Error Rates
Arsin(sqrt) transformation of 1st 54 Attributes
and sqrt() transformation for last 3 Attributes
Gaussian - 1st 54 & Log Normal - last 3 Attributes
----------------------------------------------------
Not Spam Spam | TOTAL
73/2788= 2.6% 602/1813=33.2% | 675/4601=14.7%
----------------------------------------------------

