Performs nonparametric hazard rate estimation using kernel functions and quasi-likelihoods.
Synopsis
#include <imsls.h>
float
*imsls_f_nonparam_hazard_rate
(int n_observations,
float
t[],
int n_hazard, float
hazard_min,
float hazard_increment, ...,
0)
The type double function is imsls_d_nonparam_hazard_rate.
Required Arguments
int n_observations
(Input)
Number of observations.
float t[]
(Input)
An array of n_observations
containing the failure times. If optional argument IMSLS_CENSOR_CODES is
used, the values of t may be treated as
exact failure times, as right-censored times, or a combination of exact and
right censored times. By default, all times in t are assumed to be
exact failure times.
int n_hazard
(Input)
Number of grid points at which to compute the hazard. The
function computes the hazard rates over the range given by:
hazard_min + j
* hazard_increment, for j = 0, …, n_hazard − 1.
float hazard_min
(Input)
First grid value.
float hazard_increment
(Input)
Increment between grid values.
Return Value
Pointer to an array of length n_hazard containing the estimated hazard rates.
Synopsis with Optional Arguments
#include <imsls.h>
float *imsls_f_nonparam_hazard_rate (int n_observations, float t[], int n_hazard, float hazard_min, float hazard_increment
IMSLS_PRINT_LEVEL, int iprint,
IMSLS_CENSOR_CODES, int censor_codes[],
IMSLS_WEIGHT, int iwto,
IMSLS_SORT_OPTION, int isort,
IMSLS_K_GRID, int n_k, int k_min, int k_increment,
IMSLS_BETA_GRID, int n_beta_grid, float beta_start, float beta_increment,
IMSLS_N_MISSING, int *nmiss,
IMSLS_ALPHA, float *alpha,
IMSLS_BETA, float *beta,
IMSLS_CRITERION, float *vml,
IMSLS_K, int *k,
IMSLS_SORTED_EVENT_TIMES, float **event_times,
IMSLS_SORTED_EVENT_TIMES_USER, float event_times[],
IMSLS_SORTED_CENSOR_CODES, int **isorted_censor,
IMSLS_SORTED_CENSOR_CODES_USER, int isorted_censor[],
IMSLS_RETURN_USER, float haz[],
0)
Optional Arguments
IMSLS_PRINT_LEVEL,
int iprint (Input)
Printing option.
Default: iprint = 0.
|
iprint |
Action |
|
0 |
No printing is performed. |
|
1 |
The grid estimates and the optimized estimates are printed for each value of k. |
IMSLS_CENSOR_CODES, int censor_codes[] (Input)
censor_codes is an
array of length n_observations
containing the censoring codes for each time in t. If
censor_codes[i]=0 the
failure time t[i] is treated as an
exact time of failure. Otherwise it is treated as a right-censored time;
that is, the exact time of failure is greater than t[i].
Default: All
failure times are treated as exact times of failure with no censoring.
IMSLS_WEIGHT_OPTION, int iwto
(Input)
Weight option . If iwto = 1, then
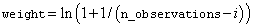is used for the i-th smallest
observation. Otherwise,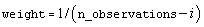 
is used.
Default: iwto = 0.
IMSLS_SORT_OPTION, int isort
(Input)
Sorting option . If isort = 1, then the
event times are not automatically sorted by the function. Otherwise, sorting is
performed with exact failure times following tied right-censored
times.
Default: isort = 0.
IMSLS_K_GRID, int n_k, int k_min, int k_increment
(Input)
Finds the optimal value of k over the range given
by: kmin + (j − 1) * k_increment, for
j = 1, …, n_k. Where n_k is the number of values of k to be
considered. k_min is the minimum
value for parameter k. k_increment is the
increment between successive values of parameter k. Parameter
k is the number of nearest neighbors to be used in computing the
k-th nearest neighbor distance.
Default: k_min is the smallest
possible value of k, k_increment =2, and
n_k will be at
most 10 points.
IMSLS_BETA_GRID, int n_beta_grid, float beta_start, float beta_increment
(Input)
For n_beta_grid > 0, a
user-defined grid is used. This grid is defined as beta_start + (j
− 1)*beta_increment, for
j = 1, …, n_beta_grid.
beta_start is
the first value to be used in the user-defined grid and beta_increment is the
increment between successive grid values of beta.
Default: The values in the initial beta search are given as follows:
Let β* = − 8, − 4, −
2, − 1, − 0.5,0.5,1, and 2, and
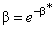
For each value of β, vml is computed at the optimizing β. The maximizing β is used to initiate the iterations. If the initial β* is determined from the search to be less than −6, then it is presumed that β is infinite, and an analytic estimate of α based upon infinite β is used. Infinite β corresponds to a flat hazard rate.
IMSLS_N_MISSING,
int *nmiss
(Output)
Number of missing (NaN, not a number) failure times in t.
IMSLS_ALPHA,
float *alpha
(Output)
Optimal estimate for the parameter α.
IMSLS_BETA,
float *beta
(Output)
Optimal estimate for the parameter β.
IMSLS_CRITERION,
float *vml
(Output)
Optimum value of the criterion function.
IMSLS_K, int
*k
(Output)
Optimal estimate for the parameter k.
IMSLS_SORTED_EVENT_TIMES,
float **event_times
(Output)
Address of a pointer to an array of length n_observations
containing the times of occurrence of the events, sorted from smallest to
largest.
IMSLS_SORTED_EVENT_TIMES_USER,
float event_times[]
(Output)
Storage for event_times is
provided by the user. See IMSLS_SORTED_EVENT_TIMES.
IMSLS_SORTED_CENSOR_CODES,
int **isorted_censor
(Output)
Address of a pointer to an array of length n_observations
containing the sorted censor codes. Censor codes are sorted corresponding
to the events event_times[i], with censored
observations preceding tied failures.
IMSLS_SORTED_CENSOR_CODES_USER,
int isorted_censor[]
(Output)
Storage for isorted_censor is
provided by the user. See IMSLS_SORTED_CENSOR_CODE.
IMSLS_RETURN_USER,
float
haz[] (Output)
If specified, haz is a user supplied array of length
n_hazard
containing the estimated hazard rates.
Description
Function imsls_f_nonparam_hazard_rate is an implementation of the methods discussed by Tanner and Wong (1984) for estimating the hazard rate in survival or reliability data with right censoring. It uses the biweight kernel,
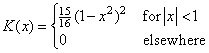
and a modified likelihood to obtain data-based estimates of
the smoothing parameters α, β, and k needed in the estimation of the
hazard rate. For kernel K(x), define the “smoothed” kernel
Ks(x −
x(j) as follows:
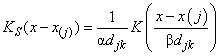
where djk is the distance to the k-th nearest failure from x(j), and x(j) is the j-th ordered observation (from smallest to largest). For given α and β, the hazard at point x is then
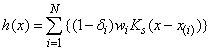
where N = n_observations, δi is the i-th observation’s censor code (1 = censored, 0 = failed), and wi is the i-th ordered observation’s weight, which may be chosen as either 1/(N − i + 1), or ln(1 + 1/(N - I + 1)). Let
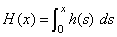
The likelihood is given by
,
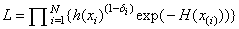where Π denotes product. Since the likelihood leads to degenerate estimates, Tanner and Wong (1984) suggest the use of a modified likelihood. The modification consists of deleting observation xi in the calculation of h(xi) and H(xi) when the likelihood term for xi is computed using the usual optimization techniques. α and β for given k can then be estimated.
Estimates for α and β are computed as follows: for given β,
a closed form solution is available for α. The problem is thus reduced to the
estimation of β.
A grid search for β is first performed. Experience
indicates that if the initial estimate of β from this grid search is greater
than, say, e6 ,then the modified
likelihood is degenerate because the hazard rate does not change with time. In
this situation, β should be taken to be infinite, and an estimate of α
corresponding to infinite β should be directly computed. When the estimate of β
from the grid search is less than e6, a secant algorithm is
used to optimize the modified likelihood. The secant algorithm iteration stops
when the change in β from one iteration to the next is less than 10−5. Alternatively, the
iterations may cease when the value of β becomes greater than e6, at which point an
infinite β with a degenerate likelihood is assumed.
To find the optimum value of the likelihood with respect to k, a user-specified grid of k-values is used. For each grid value, the modified likelihood is optimized with respect to α and β. That grid point, which leads to the smallest likelihood, is taken to be the optimal k.
Programming Notes
1. If sorting of the data is performed by imsls_f_nonparam_hazard_rate, then the sorted array will be such that all censored observations at a given time precede all failures at that time. To specify an arbitrary pattern of censored/failed observations at a given time point, the isort = 1 option must be used. In this case, it is assumed that the times have already been sorted from smallest to largest.
2. The smallest value of k must be greater than the largest number of tied failures since djk must be positive for all j. (Censored observations are not counted.) Similarly, the largest value of k must be less than the total number of failures. If the grid specified for k includes values outside the allowable range, then a warning error is issued; but k is still optimized over the allowable grid values.
3. The secant algorithm iterates on the transformed parameter β* = exp(− β). This assures a positive β, and it also seems to lead to a more desirable grid search. All results returned to the user are in the original parameterization, however.
4. Since local minimums have been observed in the modified likelihood, it is recommended that more than one grid of initial values for α and β be used.
5. Function imsls_f_nonparam_hazard_rate assumes that the hazard grid points are new data points.
Example
The following example is taken from Tanner and Wong (1984). The data are from Stablein, Carter, and Novak (1981) and involve the survival times of individuals with nonresectable gastric carcinoma. Only individuals treated with both radiation and chemotherapy are used. For each value of k from 18 to 22 with increment of 2, the default grid search for β is performed. Using the optimal value of β in the grid, the optimal parameter estimates of α and β are computed for each value of k. The final solution is the parameter estimates for the value of k which optimizes the modified likelihood (vml). Because the iprint = 1 is in effect, imsls_f_nonparam_hazard_rate prints all of the results in the output.
#include <imsls.h>
int main ()
{
int n_observations = 45, iprint = 1, kmin = 18;
int increment_k = 2, n_k = 3, isort = 1, nmiss, *isorted_censor;
float *event_times, *haz;
int n_hazard=100;
float hazard_min = 0.0, hazard_inc = 10;
float t[] = { 17.0, 42.0, 44.0, 48.0, 60.0, 72.0, 74.0, 95.0,
103.0, 108.0, 122.0, 144.0, 167.0, 170.0, 183.0,
185.0, 193.0, 195.0, 197.0, 208.0, 234.0, 235.0,
254.0, 307.0, 315.0, 401.0, 445.0, 464.0, 484.0,
528.0, 542.0, 567.0, 577.0, 580.0, 795.0, 855.0,
882.0, 892.0,1031.0,1033.0,1306.0,1335.0,1366.0,
1452.0, 1472.0};
float censor_codes[] = { 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0};
haz = imsls_f_nonparam_hazard_rate I (n_observations, t,
n_hazard, hazard_min, hazard_inc,
IMSLS_K_GRID, n_k, kmin,
increment_k,
IMSLS_PRINT_LEVEL, iprint,
IMSLS_N_MISSING, &nmiss,
IMSLS_SORT_OPTION, isort,
IMSLS_CENSOR_CODES, censor_codes,
IMSLS_SORTED_EVENT_TIMES,
&event_times,
IMSLS_SORTED_CENSOR_CODES,
&isorted_censor,
0);
printf ("\nnmiss = %d\n", nmiss);
imsls_f_write_matrix ("Sorted Event Times", 1, n_observations,
event_times, IMSLS_WRITE_FORMAT, "%7.1f", 0);
imsls_i_write_matrix ("Sorted Censors", 1, n_observations,
isorted_censor, 0);
imsls_f_write_matrix ("Hazard Rates", 1, n_hazard, haz, 0);
}
Output
*** Grid search for k = 18 ***
alpha beta vml
4.57832 2980.96 -266.805
4.54312 54.5982 -266.62
4.33646 20.0855 -265.541
4.01933 12.1825 -264.001
3.54274 7.38906 -262.54
2.99058 4.48169 -262.512
2.35154 2.71828 -262.634
1.58417 1.64872 -262.158
0.966332 1 -262.868
*** Optimal parameter estimates ***
alpha beta vml
1.69515 1.76926 -262.119
*** Grid search for k = 20 ***
alpha beta vml
4.05393 2980.96 -266.526
4.03284 54.5982 -266.401
3.90505 20.0855 -265.648
3.68782 12.1825 -264.402
3.30434 7.38906 -262.666
2.82272 4.48169 -262.08
2.25276 2.71828 -262.445
1.55578 1.64872 -261.772
0.955586 1 -262.618
*** Optimal parameter estimates ***
alpha beta vml
1.54053 1.63155 -261.771
*** Grid search for k = 22 ***
alpha beta vml
3.65641 2980.96 -267.595
3.64159 54.5982 -267.499
3.55056 20.0855 -266.904
3.38875 12.1825 -265.859
3.07147 7.38906 -264.066
2.64504 4.48169 -263.039
2.1374 2.71828 -263.335
1.51261 1.64872 -262.64
0.936368 1 -262.683
*** Optimal parameter estimates ***
alpha beta vml
1.34217 1.45001 -262.561
*** The final solution (k = 20) ***
alpha beta vml
1.54053 1.63155 -261.771
nmiss = 0
Sorted Event Times
1 2 3 4 5 6 7 8
17.0 42.0 44.0 48.0 60.0 72.0 74.0 95.0
9 10 11 12 13 14 15 16
103.0 108.0 122.0 144.0 167.0 170.0 183.0 185.0
17 18 19 20 21 22 23 24
193.0 195.0 197.0 208.0 234.0 235.0 254.0 307.0
25 26 27 28 29 30 31 32
315.0 401.0 445.0 464.0 484.0 528.0 542.0 567.0
33 34 35 36 37 38 39 40
577.0 580.0 795.0 855.0 882.0 892.0 1031.0 1033.0
41 42 43 44 45
1306.0 1335.0 1366.0 1452.0 1472.0
Sorted Censors
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
39 40 41 42 43 44 45
1 1 1 1 1 1 1
Hazard Rates
1 2 3 4 5 6
0.000962 0.001111 0.001276 0.001451 0.001634 0.001819
7 8 9 10 11 12
0.002004 0.002185 0.002359 0.002523 0.002675 0.002813
13 14 15 16 17 18
0.002935 0.003040 0.003126 0.003193 0.003240 0.003266
19 20 21 22 23 24
0.003273 0.003260 0.003229 0.003179 0.003114 0.003034
25 26 27 28 29 30
0.002941 0.002838 0.002727 0.002612 0.002495 0.002381
31 32 33 34 35 36
0.002273 0.002175 0.002084 0.001998 0.001917 0.001841
37 38 39 40 41 42
0.001771 0.001709 0.001655 0.001608 0.001569 0.001537
43 44 45 46 47 48
0.001510 0.001484 0.001459 0.001435 0.001411 0.001388
49 50 51 52 53 54
0.001365 0.001343 0.001323 0.001304 0.001285 0.001266
55 56 57 58 59 60
0.001247 0.001228 0.001208 0.001188 0.001167 0.001146
61 62 63 64 65 66
0.001125 0.001103 0.001081 0.001060 0.001040 0.001020
67 68 69 70 71 72
0.000999 0.000979 0.000958 0.000936 0.000913 0.000891
73 74 75 76 77 78
0.000868 0.000845 0.000821 0.000798 0.000775 0.000752
79 80 81 82 83 84
0.000730 0.000708 0.000685 0.000662 0.000640 0.000617
85 86 87 88 89 90
0.000595 0.000573 0.000552 0.000530 0.000510 0.000490
91 92 93 94 95 96
0.000471 0.000452 0.000434 0.000416 0.000399 0.000383
97 98 99 100
0.000366 0.000351 0.000336 0.000321
Fatal Errors
IMSLS_ALL_OBSERVATIONS_MISSING All observations are missing (NaN, not a number) values.
