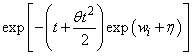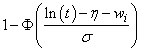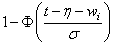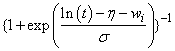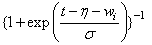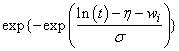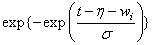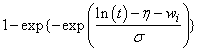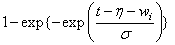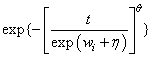Estimates survival probabilities and hazard rates for the various parametric models.
Synopsis
#include <imsls.h>
int *imsls_f_survival_estimates (Imsls_f_survival *survival_info, int n_observations, float xpt[], float time, int npt, float delta, ..., 0)
The type double function is imsls_d_survival_estimates.
Required Arguments
Imsls_f_survival
*survival_info (Input)
Pointer to structure of type
Imsls_f_survival containing the estimated survival coefficients and
other related information. See imsls_f_survival_glm.
int
n_observations (Input)
Number of observations for which
estimates are to be calculated.
float xpt[]
(Input)
Array xpt is an array of
size n_observations by x_col_dim containing the groups of covariates for
which estimates are desired, where x_col_dim is described
in the documentation for imsls_f_survival_glm. The covariates must be
specified exactly as in the call to imsls_f_survival_glm
which produced survival_info.
float time
(Input)
Beginning of the time grid for which estimates are desired. Survival
probabilities and hazard rates are computed for each covariate vector over the
grid of time points time + i*delta for
i = 0, 1, …, npt − 1.
int npt
(Input)
Number of points on the time grid for which survival probabilities
are desired.
float delta
(Input)
Increment between time points on the time grid.
Return Value
An array of size npt by (2 ∗ n_observations + 1) containing the estimated survival probabilities for the covariate groups specified in xpt. Column 0 contains the survival time. Columns 1 and 2 contain the estimated survival probabilities and hazard rates, respectively, for the covariates in the first row of xpt. In general, the survival and hazard for row i of xpt is contained in columns 2i − 1 and 2i, respectively, for i = 1, 2, …, npt.
Synopsis with Optional Arguments
#include <imsls.h>
int
*imsls_f_survival_estimates (Imsls_f_survival
survival_info,
int n_observations,
float xpt[],
float
time,
int
npt,
float delta,
IMSLS_XBETA,
float
**xbeta,
IMSLS_XBETA_USER,
float
xbeta[],
IMSLS_RETURN_USER,
float
sprob[],
0)
Optional Arguments
IMSLS_XBETA, float **xbeta
(Output)
Address of a pointer to an array of length n_observations
containing the estimated linear response
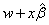
for each row of xpt.
IMSLS_XBETA_USER, float xbeta[]
(Output)
Storage for array xbeta is provided by
the user. See IMSLS_XBETA.
IMSLS_RETURN_USER, float sprob[]
(Output)
User supplied array of size npt by (2 ∗ n_observations + 1)
containing the estimated survival probabilities for the covariate groups
specified in xpt. Column 0 contains
the survival time. Columns 1 and 2 contain the estimated survival probabilities
and hazard rates, respectively, for the covariates in the first row of xpt. In general, the
survival and hazard for row i of xpt is contained in
columns 2i − 1 and
2i, respectively, for i = 1, 2, …, npt.
Description
Function imsls_f_survival_estimates computes estimates of survival probabilities and hazard rates for the parametric survival/reliability models fit by function imsls_f_survival_glm.
Let η = xTβ be the linear parameterization, where x is the design vector corresponding to a row of xpt (imsls_f_survival_estimates generates the design vector using function imsls_f_regressors_for_glm), and β is a vector of parameters associated with the linear model. Let T denote the random response variable and S(t) denote the probability that T > t. All models considered also allow a fixed parameter w (input in column ifix of xpt). Use of the parameter is discussed in function imsls_f_survival_glm. There also may be nuisance paramseters θ > 0 or σ > 0. Let Φ denote the cumulative normal distribution. The survival models available in imsls_f_survival_estimates are:
|
Model |
Name |
S (t) |
|
0 |
Exponential |
exp [−t exp (wi + η)] |
|
1 |
Linear hazard |
|
|
2 |
Log-normal |
|
|
3 |
Normal |
|
|
4 |
Log-logistic |
|
|
5 |
Logistic |
|
|
6 |
Log least extreme value |
|
|
7 |
Least extreme value |
|
|
8 |
Log extreme value |
|
|
9 |
Extreme value |
|
|
10 |
Weibull |
|
Let λ(t) denote the hazard rate at time t. Then λ(t) and S(t) are related at
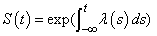
Models 0, 1, 2, 4, 6, 8, and 10 require that T > 0 (in which case assume λ(s) = 0 for s < 0), while the remaining models allow arbitrary values for T, −∞ < T < ∞. The computations proceed in function imsls_f_survival_estimates as follows:
1. The input arguments are checked for consistency and validity.
2. For each row of xpt, the explanatory variables are generated from the classification and variables and the covariates using function imsls_f_regressors_for_glm (See Chapter 2, “Regression”) with dummy_method = IMSLS_LEAVE_OUT_LAST. Given the explanatory variables x, η is computed as η = xTβ, where β is input in survival_info.
3. For each point requested in the time grid, the survival probabilities and hazard rates are computed.
Example
This example is a continuation of the first example given for function imsls_f_survival_glm. Prior to calling survival_estimates, imsls_f_survival_glm is invoked to compute the parameter estimates (contained in the structure survival_info). The example is taken from Lawless (1982, p. 287) and involves the mortality of patients suffering from lung cancer.
#include <imsls.h>
#include <stdlib.h>
int main() {
static float x[40][7] = {
1.0, 0.0, 7.0, 64.0, 5.0, 411.0, 0.0,
1.0, 0.0, 6.0, 63.0, 9.0, 126.0, 0.0,
1.0, 0.0, 7.0, 65.0, 11.0, 118.0, 0.0,
1.0, 0.0, 4.0, 69.0, 10.0, 92.0, 0.0,
1.0, 0.0, 4.0, 63.0, 58.0, 8.0, 0.0,
1.0, 0.0, 7.0, 48.0, 9.0, 25.0, 1.0,
1.0, 0.0, 7.0, 48.0, 11.0, 11.0, 0.0,
2.0, 0.0, 8.0, 63.0, 4.0, 54.0, 0.0,
2.0, 0.0, 6.0, 63.0, 14.0, 153.0, 0.0,
2.0, 0.0, 3.0, 53.0, 4.0, 16.0, 0.0,
2.0, 0.0, 8.0, 43.0, 12.0, 56.0, 0.0,
2.0, 0.0, 4.0, 55.0, 2.0, 21.0, 0.0,
2.0, 0.0, 6.0, 66.0, 25.0, 287.0, 0.0,
2.0, 0.0, 4.0, 67.0, 23.0, 10.0, 0.0,
3.0, 0.0, 2.0, 61.0, 19.0, 8.0, 0.0,
3.0, 0.0, 5.0, 63.0, 4.0, 12.0, 0.0,
4.0, 0.0, 5.0, 66.0, 16.0, 177.0, 0.0,
4.0, 0.0, 4.0, 68.0, 12.0, 12.0, 0.0,
4.0, 0.0, 8.0, 41.0, 12.0, 200.0, 0.0,
4.0, 0.0, 7.0, 53.0, 8.0, 250.0, 0.0,
4.0, 0.0, 6.0, 37.0, 13.0, 100.0, 0.0,
1.0, 1.0, 9.0, 54.0, 12.0, 999.0, 0.0,
1.0, 1.0, 5.0, 52.0, 8.0, 231.0, 1.0,
1.0, 1.0, 7.0, 50.0, 7.0, 991.0, 0.0,
1.0, 1.0, 2.0, 65.0, 21.0, 1.0, 0.0,
1.0, 1.0, 8.0, 52.0, 28.0, 201.0, 0.0,
1.0, 1.0, 6.0, 70.0, 13.0, 44.0, 0.0,
1.0, 1.0, 5.0, 40.0, 13.0, 15.0, 0.0,
2.0, 1.0, 7.0, 36.0, 22.0, 103.0, 1.0,
2.0, 1.0, 4.0, 44.0, 36.0, 2.0, 0.0,
2.0, 1.0, 3.0, 54.0, 9.0, 20.0, 0.0,
2.0, 1.0, 3.0, 59.0, 87.0, 51.0, 0.0,
3.0, 1.0, 4.0, 69.0, 5.0, 18.0, 0.0,
3.0, 1.0, 6.0, 50.0, 22.0, 90.0, 0.0,
3.0, 1.0, 8.0, 62.0, 4.0, 84.0, 0.0,
4.0, 1.0, 7.0, 68.0, 15.0, 164.0, 0.0,
4.0, 1.0, 3.0, 39.0, 4.0, 19.0, 0.0,
4.0, 1.0, 6.0, 49.0, 11.0, 43.0, 0.0,
4.0, 1.0, 8.0, 64.0, 10.0, 340.0, 0.0,
4.0, 1.0, 7.0, 67.0, 18.0, 231.0, 0.0};
int n_observations = 40;
int n_estimates = 2;
int n_class = 2;
int n_continuous = 3;
int model = 0;
int icen = 6, ilt = -1, irt = 5;
int lp_max = 40;
float time = 10.0;
int npt = 10;
float delta = 20.0;
int n_coef;
float *sprob;
Imsls_f_survival *survival_info;
char *fmt = "%12.2f%10.4f%10.6f%10.4f%10.6f";
char *clabels[] = {"", "Time", "S1", "H1", "S2", "H2"};
n_coef = imsls_f_survival_glm(n_observations, n_class,
n_continuous,
model, &x[0][0],
IMSLS_X_COL_CENSORING, icen, ilt, irt,
IMSLS_INFINITY_CHECK, lp_max,
IMSLS_SURVIVAL_INFO, &survival_info,
0);
sprob = imsls_f_survival_estimates(survival_info, n_estimates,
&x[0][0], time, npt, delta, 0);
imsls_f_write_matrix("Survival and Hazard Estimates",
npt, 2*n_estimates+1, sprob,
IMSLS_WRITE_FORMAT, fmt, IMSLS_NO_ROW_LABELS,
IMSLS_COL_LABELS, clabels, 0);
imsls_free (survival_info);
imsls_free (sprob);
}
Output
Survival and Hazard Estimates
Time S1 H1 S2 H2
10.00 0.9626 0.003807 0.9370 0.006503
30.00 0.8921 0.003807 0.8228 0.006503
50.00 0.8267 0.003807 0.7224 0.006503
70.00 0.7661 0.003807 0.6343 0.006503
90.00 0.7099 0.003807 0.5570 0.006503
110.00 0.6579 0.003807 0.4890 0.006503
130.00 0.6096 0.003807 0.4294 0.006503
150.00 0.5649 0.003807 0.3770 0.006503
170.00 0.5235 0.003807 0.3310 0.006503
190.00 0.4852 0.003807 0.2907 0.006503
Note that the hazard rate is constant over time for the exponential model.
Warning Errors
IMSLS_CONVERGENCE_ASSUMED_1 Too many step halvings. Convergence is assumed.
IMSLS_CONVERGENCE_ASSUMED_2 Too many step iterations. Convergence is assumed.
IMSLS_NO_PREDICTED_1 “estimates[0]” > 1.0. The expected value for the log logistic distribution (“model” = 4) does not exist. Predicted values will not be calculated.
IMSLS_NO_PREDICTED_2 “estimates[0]” > 1.0. The expected value for the log extreme value distribution (“model” = 8) does not exist. Predicted values will not be calculated.
IMSLS_NEG_EIGENVALUE The Hessian has at least one negative eigenvalue. An upper bound on the absolute value of the minimum eigenvalue is # corresponding to variable index #.
IMSLS_INVALID_FAILURE_TIME_4 “x[#][“ilt”= #]” = # and “x[#][“irt”= #]” = #. The censoring interval has length 0.0. The censoring code for this observation is being set to 0.0.
Fatal Error
IMSLS_MAX_CLASS_TOO_SMALL The number of distinct values of the classification variables exceeds “max_class” = #.
IMSLS_TOO_FEW_COEF IMSLS_INITIAL_EST_INPUT is specified, and “n_coef_input” = #. The model specified requires # coefficients.
IMSLS_TOO_FEW_VALID_OBS “n_observations” = %(i1) and “n_rows_missing” = #. “n_observations”−”n_rows_missing” must be greater than or equal to 2 in order to estimate the coefficients.
IMSLS_SVGLM_1 For the exponential model (“model” = 0) with “n_effects” = # and no intercept, “n_coef” has been determined to equal 0. With no coefficients in the model, processing cannot continue.
IMSLS_INCREASE_LP_MAX Too many observations are to be deleted from the model. Either use a different model or increase the workspace.
IMSLS_INVALID_DATA_8 “n_class_values[#]” = #. The number of distinct values for each classification variable must be greater than one.