Computes statistics for mean and variance inferences using samples from two normal populations.
Synopsis
#include <imsls.h>
float imsls_f_normal_two_sample (int n1_observations, float x1[], int n2_observations, float x2[], ..., 0)
The type double function is imsls_d_normal_two_sample.
Required Arguments
int
n1_observations (Input)
Number of observations in the
first sample, x1.
float x1[]
(Input)
Array of length n1_observations
containing the first sample.
int
n2_observations (Input)
Number of observations in the
second sample, x2.
float x2[]
(Input)
Array of length n2_observations
containing the second sample.
Return Value
Difference in means, x1_mean − x2_mean.
Synopsis with Optional Arguments
#include <imsls.h>
float imsls_f_normal_two_sample (int n1_observations, float x1[], int n2_observations, float x2[],
IMSLS_MEANS, float *x1_mean, float *x2_mean,
IMSLS_CONFIDENCE_MEAN, float confidence_mean,
IMSLS_CI_DIFF_FOR_EQUAL_VARS, float *lower_limit, float *upper_limit,
IMSLS_CI_DIFF_FOR_UNEQUAL_VARS, float *lower_limit, float *upper_limit
IMSLS_T_TEST_FOR_EQUAL_VARS, int *df, float *t, float *p_value,
IMSLS_T_TEST_FOR_UNEQUAL_VARS, float *df, float *t, float *p_value,
IMSLS_T_TEST_NULL, float mean_hypothesis_value,
IMSLS_POOLED_VARIANCE, float *pooled_variance,
IMSLS_CONFIDENCE_VARIANCE, float confidence_variance,
IMSLS_CI_COMMON_VARIANCE, float *lower_limit, float *upper_limit,
IMSLS_CHI_SQUARED_TEST, int *df, float *chi_squared, float *p_value,
IMSLS_CHI_SQUARED_TEST_NULL, float variance_hypothesis_value,
IMSLS_STD_DEVS, float *x1_std_dev, float *x2_std_dev,
IMSLS_CI_RATIO_VARIANCES, float *lower_limit, float *upper_limit,
IMSLS_F_TEST, int *df_numerator, int *df_denominator, float *F, float *p_value,
0)
Optional Arguments
IMSLS_MEANS, float *x1_mean, float *x2_mean
(Output)
Means of the first and second samples.
IMSLS_CONFIDENCE_MEAN, float
confidence_mean (Input)
Confidence level for two-sided
interval estimate of the mean of x1 minus the mean of
x2, in percent.
Argument confidence_mean must
be between 0.0 and 100.0 and is often 90.0, 95.0, or 99.0. For a one-sided
confidence interval with confidence level c (at least 50 percent), set
confidence_mean = 100.0 − 2.0 × (100.0 − c).
Default:
confidence_mean = 95.0
IMSLS_CI_DIFF_FOR_EQUAL_VARS, float *lower_limit, float *upper_limit
(Output)
Argument lower_limit contains
the lower confidence limit, and upper_limit contains
the upper limit for the mean of the first population minus the mean of the
second, assuming equal variances.
IMSLS_CI_DIFF_FOR_UNEQUAL_VARS, float *lower_limit, float *upper_limit
(Output)
Argument lower_limit contains
the approximate lower confidence limit, and upper_limit contains
the approximate upper limit for the mean of the first population minus the mean
of the second, assuming unequal variances.
IMSLS_T_TEST_FOR_EQUAL_VARS, int *df, float *t, float *p_value
(Output)
A t test for μ1 − μ2 = c, where c is
the null hypothesis value. (See the description of IMSLS_T_TEST_NULL.)
Argument df
contains the degrees of freedom, argument t contains the
t value, and argument p_value contains the
probability of a larger t in absolute value, assuming equal means. This
test assumes equal variances.
IMSLS_T_TEST_FOR_UNEQUAL_VARS, float *df, float *t, float *p_value
(Output)
A t test for μ1 − μ2 = c, where c is
the null hypothesis value. (See the description of IMSLS_T_TEST_NULL.)
Argument df
contains the degrees of freedom for Satterthwaite’s approximation, argument
t contains the
t value, and argument p_value contains the
approximate probability of a larger t in absolute value, assuming equal
means. This test does not assume equal variances.
IMSLS_T_TEST_NULL, float
mean_hypothesis_value (Input)
Null hypothesis value for
the t test.
Default: mean_hypothesis_value = 0.0
IMSLS_POOLED_VARIANCE, float
*pooled_variance (Output)
Pooled variance for the two
samples.
IMSLS_CONFIDENCE_VARIANCE, float
confidence_variance (Input)
Confidence level for inference
on variances. Under the assumption of equal variances, the pooled variance is
used to obtain a two-sided confidence_variance
percent confidence interval for the common variance if IMSLS_CI_COMMON_VARIANCE
is specified. Without making the assumption of equal variances, the ratio of the
variances is of interest. A two-sided confidence_variance
percent confidence interval for the ratio of the variance of the first sample to
that of the second sample is computed and is returned if IMSLS_CI_RATIO_VARIANCES
is specified. The confidence intervals are symmetric in probability.
Default: confidence_variance = 95.0
IMSLS_CI_COMMON_VARIANCE, float *lower_limit, float *upper_limit
(Output)
Argument lower_limit contains
the lower confidence limit, and upper_limit contains
the upper limit for the common, or pooled, variance.
IMSLS_CHI_SQUARED_TEST, int *df, float *chi_squared, float *p_value
(Output)
The chi-squared test for
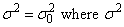
is the common, or pooled, variance, and
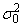
is the null hypothesis value. (See description of IMSLS_CHI_SQUARED_TEST_NULL.) Argument df contains the degrees of freedom, argument chi_squared contains the chi-squared value, and argument p_value contains the probability of a larger chi-squared in absolute value, assuming equal means.
IMSLS_CHI_SQUARED_TEST_NULL, float
variance_hypothesis_value (Input)
Null hypothesis value
for the chi-squared test.
Default: variance_hypothesis_value = 1.0
IMSLS_STD_DEVS, float *x1_std_dev, float
*x2_std_dev (Output)
Standard deviations of the first and
second samples.
IMSLS_CI_RATIO_VARIANCES, float *lower_limit, float *upper_limit
(Output)
Argument lower_limit contains
the approximate lower confidence limit, and upper_limit contains
the approximate upper limit for the ratio of the variance of the first
population to the second.
IMSLS_F_TEST, int *df_numerator, int *df_denominator, float *F, float *p_value
(Output)
The F test for equality of variances. Argument df_numerator and df_denominator contain
the numerator degrees of freedom, argument F contains the
F test value, and argument p_value contains the
probability of a larger F in absolute value, assuming equal
variances.
Description
Function imsls_f_normal_two_sample computes statistics for making inferences about the means and variances of two normal populations, using independent samples in x1 and x2. For inferences concerning parameters of a single normal population, see function imsls_f_normal_one_sample.
Let μ1 and 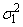 be the mean and variance of the
first population, and let μ2 and
be the mean and variance of the
first population, and let μ2 and 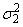 be the corresponding quantities
of the second population. The function contains test confidence intervals for
difference in means, equality of variances, and the pooled variance.
be the corresponding quantities
of the second population. The function contains test confidence intervals for
difference in means, equality of variances, and the pooled variance.
The means and variances for the two samples are as follows:

and
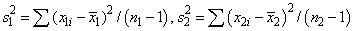
Inferences about the Means
The test that the difference in means equals a certain value, for example, μ0, depends on whether or not the variances of the two populations can be considered equal. If the variances are equal and mean_hypothesis_value equals 0, the test is the two-sample t test, which is equivalent to an analysis-of-variance test. The pooled variance for the difference-in-means test is as follows:
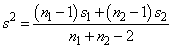
The t statistic is as follows:
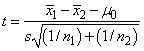
Also, the confidence interval for the difference in means can be obtained by specifying IMSLS_CI_DIFF_FOR_EQUAL_VARS.
If the population variances are not equal, the ordinary t statistic does not have a t distribution and several approximate tests for the equality of means have been proposed. (See, for example, Anderson and Bancroft 1952, and Kendall and Stuart 1979.) One of the earliest tests devised for this situation is the Fisher-Behrens test, based on Fisher’s concept of fiducial probability. A procedure used if IMSLS_T_TEST_FOR_UNEQUAL_VARS and/or IMSLS_CI_DIFF_FOR_UNEQUAL_VARS are specified is the Satterthwaite’s procedure, as suggested by H.F. Smith and modified by F.E. Satterthwaite (Anderson and Bancroft 1952, p. 83).
The test statistic is
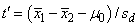
where
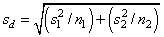
Under the null hypothesis of μ1 − μ2 = c, this quantity has an approximate t distribution with degrees of freedom df (in IMSLS_T_TEST_FOR_UNEQUAL_VARS), given by the following equation:
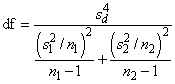
Inferences about Variances
The F statistic for testing the equality of
variances is given by 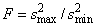 , where
, where 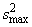 is the larger of
is the larger of 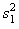 and
and 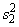 . If the variances are equal, this
quantity has an F distribution with n1 − 1 and
n2 − 1 degrees
of freedom.
. If the variances are equal, this
quantity has an F distribution with n1 − 1 and
n2 − 1 degrees
of freedom.
It is generally not recommended that the results of the F test be used to decide whether to use the regular t test or the modified tʹ on a single set of data. The modified tʹ (Satterthwaite’s procedure) is the more conservative approach to use if there is doubt about the equality of the variances.
Examples
Example 1
This example, taken from Conover and Iman (1983, p. 294), involves scores on arithmetic tests of two grade-school classes. The question is whether a group taught by an experimental method has a higher mean score. Only the difference in means is output. The data are shown below.
|
Scores for Standard Group |
Scores for Experimental Group |
|
72 |
111 |
|
75 |
118 |
|
77 |
128 |
|
80 |
138 |
|
104 |
140 |
|
110 |
150 |
|
125 |
163 |
|
|
164 |
|
|
169 |
#include <imsls.h>
int main()
{
#define N1_OBSERVATIONS 7
#define N2_OBSERVATIONS 9
float diff_means;
float x1[N1_OBSERVATIONS] = {
72.0, 75.0, 77.0, 80.0, 104.0, 110.0, 125.0};
float x2[N2_OBSERVATIONS] = {
111.0, 118.0, 128.0, 138.0, 140.0, 150.0, 163.0,
164.0, 169.0};
/* Perform analysis */
diff_means = imsls_f_normal_two_sample(N1_OBSERVATIONS, x1,
N2_OBSERVATIONS, x2, 0);
/* Print results */
printf("\nx1_mean - x2_mean = %5.2f\n", diff_means);
}
Output
x1_mean - x2_mean = -50.48
Example 2
The same data is used for this example as for the initial example. Here, the results of the t test are output. The variances of the two populations are assumed to be equal. It is seen from the output that there is strong reason to believe that the two means are different (t value of −4.804). Since the lower 97.5-percent confidence limit does not include 0, the null hypothesis is that μ1 ≤ μ 2 would be rejected at the 0.05 significance level. (The closeness of the values of the sample variances provides some qualitative substantiation of the assumption of equal variances.)
#include <imsls.h>
int main()
{
#define N1_OBSERVATIONS 7
#define N2_OBSERVATIONS 9
int df;
float diff_means, lower_limit, upper_limit, t, p_value, sp2;
float x1[N1_OBSERVATIONS] = {
72.0, 75.0, 77.0, 80.0, 104.0, 110.0, 125.0};
float x2[N2_OBSERVATIONS] = {
111.0, 118.0, 128.0, 138.0, 140.0, 150.0, 163.0,
164.0, 169.0};
/* Perform analysis */
diff_means = imsls_f_normal_two_sample(N1_OBSERVATIONS, x1,
N2_OBSERVATIONS, x2,
IMSLS_POOLED_VARIANCE, &sp2,
IMSLS_CI_DIFF_FOR_EQUAL_VARS, &lower_limit, &upper_limit,
IMSLS_T_TEST_FOR_EQUAL_VARS, &df, &t, &p_value,
0);
/* Print results */
printf("\nx1_mean - x2_mean = %5.2f\n", diff_means);
printf("Pooled variance = %5.2f\n", sp2);
printf("95%% CI for x1_mean - x2_mean is (%5.2f,%5.2f)\n",
lower_limit, upper_limit);
printf("df = %3d\n", df);
printf("t = %5.2f\n", t);
printf("p-value = %8.5f\n", p_value);
}
Output
x1_mean - x2_mean = -50.48
Pooled variance = 434.63
95% CI for x1_mean - x2_mean is (-73.01,-27.94)
df = 14
t = -4.80
p-value = 0.00028
