poly_prediction

Chapter 2: Regression > poly_prediction

poly_prediction

Computes predicted values, confidence intervals, and diagnostics after fitting a polynomial regression model.

Synopsis

#include <imsls.h>

float *imsls_f_poly_prediction (Imsls_f_poly_regression *poly_info, int n_predict, float x[], ..., 0)

The type double function is imsls_d_poly_prediction.

Required Arguments

Imsls_f_poly_regression *poly_info (Input)
Pointer to a structure of type Imsls_f_poly_regression. See function imsls_f_poly_regression.

int n_predict (Input)
Length of array x.

float x[] (Input)
Array of length n_predict containing the values of the independent variable for which calculations are to be performed.

Return Value

A pointer to an internally allocated array of length n_predict containing the predicted values.

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_poly_prediction (Imsls_f_poly_regression *poly_info, int n_predict, float x[],

IMSLS_CONFIDENCE, float confidence,

IMSLS_WEIGHTS, float weights[],

IMSLS_SCHEFFE_CI, float **lower_limit, float **upper_limit,

IMSLS_SCHEFFE_CI_USER, float lower_limit[], float upper_limit[],

IMSLS_POINTWISE_CI_POP_MEAN, float **lower_limit, float **upper_limit,

IMSLS_POINTWISE_CI_POP_MEAN_USER, float lower_limit[],

IMSLS_POINTWISE_CI_NEW_SAMPLE, float **lower_limit, float **upper_limit,

IMSLS_POINTWISE_CI_NEW_SAMPLE_USER, float lower_limit[], float upper_limit[],

IMSLS_LEVERAGE_USER, float leverage[],

IMSLS_RETURN_USER, float y_hat[],

IMSLS_Y, float y[],

IMSLS_RESIDUAL, float **residual,

IMSLS_RESIDUAL_USER, float residual[],

IMSLS_STANDARDIZED_RESIDUAL, float **standardized_residual,

IMSLS_STANDARDIZED_RESIDUAL_USER, float standardized_residual[],

IMSLS_DELETED_RESIDUAL, float **deleted_residual,

IMSLS_DELETED_RESIDUAL_USER, float deleted_residual[],

IMSLS_COOKSD, float **cooksd,

IMSLS_COOKSD_USER, float cooksd[],

IMSLS_DFFITS, float **dffits,

IMSLS_DFFITS_USER, float dffits[],

Optional Arguments

IMSLS_CONFIDENCE, float confidence (Input)
Confidence level for both two-sided interval estimates on the mean and for two-sided prediction intervals in percent. Argument confidence must be in the range [0.0, 100.0). For one-sided intervals with confidence level onecl, where 50.0 ≤ onecl < 100.0, set confidence = 100.0 – 2.0 * (100.0 − onecl).
Default: confidence = 95.0.

IMSLS_WEIGHTS, float weights[] (Input)
Array of length n_predict containing the weight for each row of x. The computed prediction interval uses SSE/(DFE*weights[i]) for the estimated variance of a future response.
Default: weights[] = 1.

IMSLS_SCHEFFE_CI, float **lower_limit, float **upper_limit (Output)
Array lower_limit is the address of a pointer to an internally allocated array of length n_predict containing the lower confidence limits of Scheffé confidence intervals corresponding to the rows of x. Array upper_limit is the address of a pointer to an internally allocated array of length n_predict containing the upper confidence limits of Scheffé confidence intervals corresponding to the rows of x.

IMSLS_SCHEFFE_CI_USER, float lower_limit[], float upper_limit[] (Output)
Storage for arrays lower_limit and upper_limit is provided by the user. See IMSLS_SCHEFFE_CI.

IMSLS_POINTWISE_CI_POP_MEAN, float **lower_limit, float **upper_limit (Output)
Array lower_limit is the address of a pointer to an internally allocated array of length n_predict containing the lower confidence limits of the confidence intervals for two-sided interval estimates of the means, corresponding to the rows of x. Array upper_limit is the address of a pointer to an internally allocated array of length n_predict containing the upper confidence limits of the confidence intervals for two-sided interval estimates of the means, corresponding to the rows
of x.

IMSLS_POINTWISE_CI_POP_MEAN_USER, float lower_limit[], float upper_limit[] (Output)
Storage for arrays lower_limit and upper_limit is provided by the user. See IMSLS_POINTWISE_CI_POP_MEAN.

IMSLS_POINTWISE_CI_NEW_SAMPLE, float **lower_limit, float **upper_limit (Output)
Array lower_limit is the address of a pointer to an internally allocated array of length n_predict containing the lower confidence limits of the confidence intervals for two-sided prediction intervals, corresponding to the rows of x. Array upper_limit is the address of a pointer to an internally allocated array of length n_predict containing the upper confidence limits of the confidence intervals for two-sided prediction intervals, corresponding to the rows of x.

IMSLS_POINTWISE_CI_NEW_SAMPLE_USER, float lower_limit[], float upper_limit[] (Output)
Storage for arrays lower_limit and upper_limit is provided by the user. See IMSLS_POINTWISE_CI_NEW_SAMPLE.

IMSLS_LEVERAGE, float **leverage (Output)
Address of a pointer to an internally allocated array of length n_predict containing the leverages.

IMSLS_LEVERAGE_USER, float leverage[] (Output)
Storage for array leverage is provided by the user. See IMSLS_LEVERAGE.

IMSLS_RETURN_USER, float y_hat[] (Output)
Storage for array y_hat is provided by the user. The length n_predict array contains the predicted values.

IMSLS_Y float y[] (Input)
Array of length n_predict containing the observed responses.

Note: IMSLS_Y must be specified if any of the following optional arguments are specified.

IMSLS_RESIDUAL, float **residual (Output)
Address of a pointer to an internally allocated array of length n_predict containing the residuals.

IMSLS_RESIDUAL_USER, float residual[] (Output)
Storage for array residual is provided by the user. See IMSLS_RESIDUAL.

IMSLS_STANDARDIZED_RESIDUAL, float **standardized_residual (Output)
Address of a pointer to an internally allocated array of length n_predict containing the standardized residuals.

IMSLS_STANDARDIZED_RESIDUAL_USER, float standardized_residual[] (Output)
Storage for array standardized_residual is provided by the user. See IMSLS_STANDARDIZED_RESIDUAL.

IMSLS_DELETED_RESIDUAL, float **deleted_residual (Output)
Address of a pointer to an internally allocated array of length n_predict containing the deleted residuals.

IMSLS_DELETED_RESIDUAL_USER, float deleted_residual[] (Output)
Storage for array deleted_residual is provided by the user. See IMSLS_DELETED_RESIDUAL.

IMSLS_COOKSD, float **cooksd (Output)
Address of a pointer to an internally allocated array of length n_predict containing the Cook’s D statistics.

IMSLS_COOKSD_USER, float cooksd[] (Output)
Storage for array cooksd is provided by the user. See IMSLS_COOKSD.

IMSLS_DFFITS, float **dffits (Output)
Address of a pointer to an internally allocated array of length n_predict containing the DFFITS statistics.

IMSLS_DFFITS_USER, float dffits[] (Output)
Storage for array dffits is provided by the user. See IMSLS_DFFITS.

Description

Function imsls_f_poly_prediction assumes a polynomial model

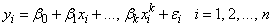
where the observed values of the y_i’s constitute the response, the x_i’s are the settings of the independent variable, the β_j’s are the regression coefficients and the ɛ_i’s are the errors that are independently distributed normal with mean 0 and the following variance:

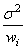
Given the results of a polynomial regression, fitted using orthogonal polynomials and weights w_i, function imsls_f_poly_prediction produces predicted values, residuals, confidence intervals, prediction intervals, and diagnostics for outliers and in influential cases.

Often, a predicted value and confidence interval are desired for a setting of the independent variable not used in computing the regression fit. This is accomplished by simply using a different x matrix when calling imsls_f_poly_prediction than was used for the fit (function imsls_f_poly_regression). See Example 1.

Results from function imsls_f_poly_regression, which produces the fit using orthogonal polynomials, are used for input by the structure poly_info. The fitted model from imsls_f_poly_regression is

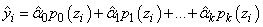
where the z_i’s are settings of the independent variable x scaled to the interval [−2, 2] and the p_j (z)’s are the orthogonal polynomials. The X^TX matrix for this model is a diagonal matrix with elements d_j. The case statistics are easily computed from this model and are equal to those from the original polynomial model with β_j’s as the regression coefficients.

The leverage is computed as follows:

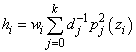
The estimated variance of

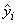
is given by the following:

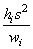
The computation of the remainder of the case statistics follows easily from the definitions. See Diagnostics for Individual Cases” for the definition of the case diagnostics.

Often, predicted values and confidence intervals are desired for combinations of settings of the independent variables not used in computing the regression fit. This can be accomplished by defining a new data matrix. Since the information about the model fit is input in poly_info, it is not necessary to send in the data set used for the original calculation of the fit, i.e., only variable combinations for which predictions are desired need be entered in x.

Examples

Example 1

A polynomial model is fit to the data discussed by Neter and Wasserman (1974, pp. 279–285). The data set contains the response variable y measuring coffee sales (in hundred gallons) and the number of self-service dispensers. Responses for 14 similar cafeterias are in the data set.

#include <imsls.h>

int main()

{

Imsls_f_poly_regression *poly_info;

float *y_hat, *coefficients;

int n_observations = 14;

int degree = 2;

int n_predict = 8;

float x[] = {0.0, 0.0, 1.0, 1.0, 2.0, 2.0, 4.0,

4.0, 5.0, 5.0, 6.0, 6.0, 7.0, 7.0};

float y[] = {508.1, 498.4, 568.2, 577.3, 651.7, 657.0, 755.3,

758.9, 787.6, 792.1, 841.4, 831.8, 854.7, 871.4};

float x2[] = {0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0};

/* Generate the polynomial regression fit*/

coefficients = imsls_f_poly_regression (n_observations, x, y,

degree, IMSLS_POLY_REGRESSION_INFO, &poly_info, 0);

/* Compute predicted values */

y_hat = imsls_f_poly_prediction(poly_info, n_predict, x2, 0);

/* Print predicted values */

imsls_f_write_matrix("Predicted Values", 1, n_predict, y_hat, 0);

imsls_free(coefficients);

imsls_free(y_hat);

return;

}

Output

Predicted Values

1 2 3 4 5 6

503.3 578.3 645.4 704.4 755.6 798.8

7 8

834.1 861.4

Example 2

Predicted values, confidence intervals, and diagnostics are computed for the data set described in the first example.

#include <imsls.h>

int main()

{

#define N_PREDICT 14

Imsls_f_poly_regression *poly_info;

float *coefficients, y_hat[N_PREDICT],

lower_ci[N_PREDICT], upper_ci[N_PREDICT],

lower_pi[N_PREDICT], upper_pi[N_PREDICT],

s_residual[N_PREDICT], d_residual[N_PREDICT],

leverage[N_PREDICT], cooksd[N_PREDICT],

dffits[N_PREDICT], lower_scheffe[N_PREDICT],

upper_scheffe[N_PREDICT];

int n_observations = N_PREDICT;

int degree = 2;

float x[] = {0.0, 0.0, 1.0, 1.0, 2.0, 2.0, 4.0,

4.0, 5.0, 5.0, 6.0, 6.0, 7.0, 7.0};

float y[] = {508.1, 498.4, 568.2, 577.3, 651.7, 657.0, 755.3,

758.9, 787.6, 792.1, 841.4, 831.8, 854.7, 871.4};

/* Generate the polynomial regression fit*/

coefficients = imsls_f_poly_regression (n_observations, x, y,

degree, IMSLS_POLY_REGRESSION_INFO, &poly_info, 0);

/* Compute predicted values and case statistics */

imsls_f_poly_prediction(poly_info, N_PREDICT, x,

IMSLS_RETURN_USER, y_hat,

IMSLS_POINTWISE_CI_POP_MEAN_USER, lower_ci, upper_ci,

IMSLS_POINTWISE_CI_NEW_SAMPLE_USER, lower_pi, upper_pi,

IMSLS_Y, y,

IMSLS_STANDARDIZED_RESIDUAL_USER, s_residual,

IMSLS_DELETED_RESIDUAL_USER, d_residual,

IMSLS_LEVERAGE_USER, leverage,

IMSLS_COOKSD_USER, cooksd,

IMSLS_DFFITS_USER, dffits,

IMSLS_SCHEFFE_CI_USER, lower_scheffe, upper_scheffe,

0);

/* Print results */

imsls_f_write_matrix("Predicted Values", 1, N_PREDICT, y_hat, 0);

imsls_f_write_matrix("Lower Scheffe CI", 1, N_PREDICT,

lower_scheffe, 0);

imsls_f_write_matrix("Upper Scheffe CI", 1, N_PREDICT,

upper_scheffe, 0);

imsls_f_write_matrix("Lower CI", 1, N_PREDICT, lower_ci, 0);

imsls_f_write_matrix("Upper CI", 1, N_PREDICT, upper_ci, 0);

imsls_f_write_matrix("Lower PI", 1, N_PREDICT, lower_pi, 0);

imsls_f_write_matrix("Upper PI", 1, N_PREDICT, upper_pi, 0);

imsls_f_write_matrix("Standardized Residual", 1, N_PREDICT,

s_residual, 0);

imsls_f_write_matrix("Deleted Residual", 1, N_PREDICT,

d_residual, 0);

imsls_f_write_matrix("Leverage", 1, N_PREDICT, leverage, 0);

imsls_f_write_matrix("Cooks Distance", 1, N_PREDICT, cooksd, 0);

imsls_f_write_matrix("DFFITS", 1, N_PREDICT, dffits, 0);

imsls_free(coefficients);

return;

}

Output

Predicted Values

1 2 3 4 5 6

503.3 503.3 578.3 578.3 645.4 645.4

7 8 9 10 11 12

755.6 755.6 798.8 798.8 834.1 834.1

13 14

861.4 861.4

Lower Scheffe CI

1 2 3 4 5 6

489.8 489.8 569.5 569.5 636.5 636.5

7 8 9 10 11 12

745.7 745.7 790.2 790.2 825.5 825.5

13 14

847.7 847.7

Upper Scheffe CI

1 2 3 4 5 6

516.9 516.9 587.1 587.1 654.2 654.2

7 8 9 10 11 12

765.5 765.5 807.4 807.4 842.7 842.7

13 14

875.1 875.1

Lower CI

1 2 3 4 5 6

492.8 492.8 571.5 571.5 638.4 638.4

7 8 9 10 11 12

747.9 747.9 792.1 792.1 827.4 827.4

13 14

850.7 850.7

Upper CI

1 2 3 4 5 6

513.9 513.9 585.2 585.2 652.3 652.3

7 8 9 10 11 12

763.3 763.3 805.5 805.5 840.8 840.8

13 14

872.1 872.1

Lower PI

1 2 3 4 5 6

482.8 482.8 559.3 559.3 626.4 626.4

7 8 9 10 11 12

736.3 736.3 779.9 779.9 815.2 815.2

13 14

840.8 840.8

Upper PI

1 2 3 4 5 6

523.9 523.9 597.3 597.3 664.3 664.3

7 8 9 10 11 12

774.9 774.9 817.7 817.7 853.0 853.0

13 14

882.1 882.1

Standardized Residual

1 2 3 4 5 6

0.737 -0.766 -1.366 -0.137 0.859 1.575

7 8 9 10 11 12

-0.041 0.456 -1.507 -0.902 0.982 -0.308

13 14

-1.051 1.557

Deleted Residual

1 2 3 4 5 6

0.720 -0.751 -1.429 -0.131 0.848 1.707

7 8 9 10 11 12

-0.039 0.439 -1.613 -0.894 0.980 -0.295

13 14

-1.056 1.681

Leverage

1 2 3 4 5 6

0.3554 0.3554 0.1507 0.1507 0.1535 0.1535

7 8 9 10 11 12

0.1897 0.1897 0.1429 0.1429 0.1429 0.1429

13 14

0.3650 0.3650

Cooks Distance

1 2 3 4 5 6

0.0997 0.1080 0.1104 0.0011 0.0446 0.1500

7 8 9 10 11 12

0.0001 0.0162 0.1262 0.0452 0.0536 0.0053

13 14

0.2116 0.4644

DFFITS

1 2 3 4 5 6

0.535 -0.558 -0.602 -0.055 0.361 0.727

7 8 9 10 11 12

-0.019 0.212 -0.659 -0.365 0.400 -0.120

13 14

-0.801 1.274

Warning Errors

IMSLS_LEVERAGE_GT_1 A leverage (= #) much greater than one is computed. It is set to 1.0.

IMSLS_DEL_MSE_LT_0 A deleted residual mean square (= #) much less than zero is computed. It is set to zero.

Fatal Errors

IMSLS_NEG_WEIGHT “weights[#]” = #. Weights must be nonnegative.

Contact Support