Generates pseudorandom numbers from a Cauchy distribution.
Synopsis
#include <imsls.h>
float *imsls_f_random_cauchy (int n_random, ..., 0)
The type double function is imsls_d_random_cauchy.
Required Arguments
int n_random
(Input)
Number of random numbers to generate.
Return Value
An array of length n_random containing the random Cauchy deviates.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_random_cauchy (int n_random,
IMSLS_RETURN_USER,
float r[],
0)
Optional Arguments
IMSLS_RETURN_USER, float r[]
(Output)
User-supplied array of length n_random containing
the random Cauchy deviates.
Description
Function imsls_f_random_cauchy generates pseudorandom numbers from a Cauchy distribution. The probability density function is
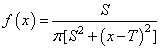
where T is the median and T − S is the first quartile. This function first generates standard Cauchy random numbers (T = 0 and S = 1) using the technique described below, and then scales the values using T and S.
Use of the inverse CDF technique would yield a Cauchy deviate from a uniform (0, 1) deviate, u, as tan [π (u − 0.5)]. Rather than evaluating a tangent directly, however, random_cauchy generates two uniform (−1, 1) deviates, x1 and x2. These values can be thought of as sine and cosine values. If
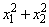
is less than or equal to 1, then x1/x2 is delivered as the unscaled Cauchy deviate; otherwise, x1 and x2 are rejected and two new uniform (−1, 1) deviates are generated. This method is also equivalent to taking the ration of two independent normal deviates.
Example
In this example, imsls_f_random_cauchy generates five pseudorandom Cauchy numbers. The generator used is a simple multiplicative congruential with a multiplier of 16807.
#include <imsls.h>
#include <stdio.h>
int main()
{
int n_random = 5;
float *r;
imsls_random_seed_set(123457);
r = imsls_f_random_cauchy(n_random, 0);
printf("Cauchy random deviates: %8.4f%8.4f%8.4f%8.4f%8.4f\n",
r[0], r[1], r[2], r[3], r[4]);
}
Output
Cauchy random deviates: 3.5765 0.9353 15.5797 2.0815 -0.1333
