Computes the ranks, normal scores, or exponential scores for a vector of observations.
Synopsis
#include <imsls.h>
float *imsls_f_ranks (int n_observations, float x[], ..., 0)
The type double function is imsls_d_ranks.
Required Arguments
int
n_observations (Input)
Number of observations.
float x[]
(Input)
Array of length n_observations
containing the observations to be ranked.
Return Value
A pointer to a vector of length n_observations containing the rank (or optionally, a transformation of the rank) of each observation.
Synopsis with Optional Arguments
#include <imsl.h>
float*
imsls_f_ranks (int
n_observations,
float
x[],
IMSLS_AVERAGE_TIE,
or
IMSLS_HIGHEST,
or
IMSLS_LOWEST,
or
IMSLS_RANDOM_SPLIT,
IMSLS_FUZZ,
float
fuzz_value,
IMSLS_RANKS,
or
IMSLS_BLOM_SCORES,
or
IMSLS_TUKEY_SCORES,
or
IMSLS_VAN_DER_WAERDEN_SCORES,
or
IMSLS_EXPECTED_NORMAL_SCORES,
or
IMSLS_SAVAGE_SCORES,
IMSLS_RETURN_USER,
float
ranks[],
0)
Optional Arguments
IMSLS_AVERAGE_TIE, or
IMSLS_HIGHEST, or
IMSLS_LOWEST, or
IMSLS_RANDOM_SPLIT
Exactly
one of these optional arguments can be used to change the method used to assign
a score to tied observations.
|
Argument |
Method |
|
IMSLS_AVERAGE_TIE |
average of the scores of the tied observations (default) |
|
IMSLS_HIGHEST |
highest score in the group of ties |
|
IMSLS_LOWEST |
lowest score in the group of ties |
|
IMSLS_RANDOM_SPLIT |
tied observations are randomly split using a random number generator |
IMSLS_FUZZ, float
fuzz_value (Input)
Value used to determine when two items
are tied. If abs(x [i] − x [j]) is less than or
equal to fuzz_value, then x[i] and x[j] are said to be
tied.
Default: fuzz_value = 0.0
IMSLS_RANKS, or
IMSLS_BLOM_SCORES, or
IMSLS_TUKEY_SCORES, or
IMSLS_VAN_DER_WAERDEN_SCORES, or
IMSLS_EXPECTED_NORMAL_SCORES, or
IMSLS_SAVAGE_SCORES
Exactly
one of these optional arguments can be used to specify the type of values
returned.
|
Argument |
Result |
|
IMSLS_RANKS |
ranks (default) |
|
IMSLS_BLOM_SCORES |
Blom version of normal scores |
|
IMSLS_TUKEY_SCORES |
Tukey version of normal scores |
|
IMSLS_VAN_DER_WAERDEN_SCORES |
Van der Waerden version of normal scores |
|
IMSLS_EXPECTED_NORMAL_SCORES |
expected value of normal order statistics (for tied observations, the average of the expected normal scores) |
|
IMSLS_SAVAGE_SCORES |
Savage scores (the expected value of exponential order statistics) |
IMSLS_RETURN_USER, float ranks[]
(Output)
If specified, the ranks are returned in the user-supplied array
ranks.
Description
Ties
In data without ties, the output values are the ordinary ranks (or a transformation of the ranks) of the data in x. If x[i] has the smallest value among the values in x and there is no other element in x with this value, then ranks [i] = 1. If both x[i] and x[j] have the same smallest value, the output value depends on the option used to break ties.
|
Argument |
Result |
|
IMSLS_AVERAGE_TIE |
ranks[i] = ranks[j] = 1.5 |
|
IMSLS_HIGHEST |
ranks[i] = ranks[j] = 2.0 |
|
IMSLS_LOWEST |
ranks[i] = ranks[j] = 1.0 |
|
IMSLS_RANDOM_SPLIT |
ranks[i] = 1.0 and ranks[j] = 2.0 or, randomly, ranks[i] = 2.0 and ranks[j] = 1.0 |
When the ties are resolved randomly, function imsls_f_random_uniform (Chapter 12;) is used to generate random numbers. Different results may occur from different executions of the program unless the “seed” of the random number generator is set explicitly by use of the function imsls_f_random_seed_set (Chapter 12;).
Scores
As an option, normal and other functions of the ranks can be returned. Normal scores can be defined as the expected values, or approximations to the expected values, of order statistics from a normal distribution. The simplest approximations are obtained by evaluating the inverse cumulative normal distribution function, function imsls_f_normal_inverse_cdf (Chapter 11;), at the ranks scaled into the open interval (0, 1). In the Blom version (see Blom 1958), the scaling transformation for the rank ri (1 ≤ ri ≤ n, where n is the sample size, n_observations) is (ri − 3/8)/(n + 1/4). The Blom normal score corresponding to the observation with rank ri is
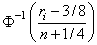
where Φ(·) is the normal cumulative distribution function.
Adjustments for ties are made after the normal score transformation. That is, if x [i] equals x [j] (within fuzz_value) and their value is the k-th smallest in the data set, the Blom normal scores are determined for ranks of k and k + 1. Then, these normal scores are averaged or selected in the manner specified. (Whether the transformations are made first or ties are resolved first makes no difference except when IMSLS_AVERAGE_TIE is specified.)
In the Tukey version (see Tukey 1962), the scaling transformation for the rank ri is (ri − 1/3)/(n + 1/3). The Tukey normal score corresponding to the observation with rank ri is as follows:
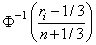
Ties are handled in the same way as for the Blom normal scores.
In the Van der Waerden version (see Lehmann 1975, p. 97), the scaling transformation for the rank ri is ri/(n + 1). The Van der Waerden normal score corresponding to the observation with rank ri is as follows:
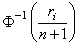
Ties are handled in the same way as for the Blom normal scores.
When option IMSLS_EXPECTED_NORMAL_SCORES is used, the output values are the expected values of the normal order statistics from a sample of size n_observations. If the value in x[i] is the k-th smallest, the value output in ranks [i] is E(zk), where E(·) is the expectation operator and zk is the k-th order statistic in a sample of size n_observations from a standard normal distribution. Ties are handled in the same way as for the Blom normal scores.
Savage scores are the expected values of the exponential order statistics from a sample of size n_observations. These values are called Savage scores because of their use in a test discussed by Savage 1956 (see also Lehmann 1975). If the value in x[i] is the k-th smallest, the value output in ranks [i] is E(yk), where yk is the k-th order statistic in a sample of size n_observations from a standard exponential distribution. The expected value of the k-th order statistic from an exponential sample of size n (n_observations) is as follows:
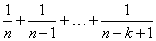
Ties are handled in the same way as for the Blom normal scores.
Examples
Example 1
The data for this example, from Hinkley (1977), contains 30 observations. Note that the fourth and sixth observations are tied and that the third and twentieth observations are tied.
#include <imsls.h>
#define N_OBSERVATIONS 30
int main()
{
float *ranks;
float x[] = {0.77, 1.74, 0.81, 1.20, 1.95, 1.20, 0.47, 1.43,
3.37, 2.20, 3.00, 3.09, 1.51, 2.10, 0.52, 1.62,
1.31, 0.32, 0.59, 0.81, 2.81, 1.87, 1.18, 1.35,
4.75, 2.48, 0.96, 1.89, 0.90, 2.05};
ranks = imsls_f_ranks(N_OBSERVATIONS, x, 0);
imsls_f_write_matrix("Ranks", 1, N_OBSERVATIONS, ranks, 0);
}
Output
Ranks
1 2 3 4 5 6
5.0 18.0 6.5 11.5 21.0 11.5
7 8 9 10 11 12
2.0 15.0 29.0 24.0 27.0 28.0
13 14 15 16 17 18
16.0 23.0 3.0 17.0 13.0 1.0
19 20 21 22 23 24
4.0 6.5 26.0 19.0 10.0 14.0
25 26 27 28 29 30
30.0 25.0 9.0 20.0 8.0 22.0
Example 2
This example uses all the score options with the same data set, which contains some ties. Ties are handled in several different ways in this example.
#include <imsls.h>
#define N_OBSERVATIONS 30
void main()
{
float fuzz_value=s0.0, score[4][N_OBSERVATIONS], *ranks;
float x[] = {0.77, 1.74, 0.81, 1.20, 1.95, 1.20, 0.47, 1.43,
3.37, 2.20, 3.00, 3.09, 1.51, 2.10, 0.52, 1.62,
1.31, 0.32, 0.59, 0.81, 2.81, 1.87, 1.18, 1.35,
4.75, 2.48, 0.96, 1.89, 0.90, 2.05};
char *row_labels[] = {"Blom", "Tukey", "Van der Waerden",
"Expected Value"};
/* Blom scores using largest ranks */
/* for ties */
imsls_f_ranks(N_OBSERVATIONS, x,
IMSLS_HIGHEST,
IMSLS_BLOM_SCORES,
IMSLS_RETURN_USER, &score[0][0],
0);
/* Tukey normal scores using smallest */
/* ranks for ties */
imsls_f_ranks(N_OBSERVATIONS, x,
IMSLS_LOWEST,
IMSLS_TUKEY_SCORES,
IMSLS_RETURN_USER, &score[1][0],
0);
/* Van der Waerden scores using */
/* randomly resolved ties */
imsls_random_seed_set(123457);
imsls_f_ranks(N_OBSERVATIONS, x,
IMSLS_RANDOM_SPLIT,
IMSLS_VAN_DER_WAERDEN_SCORES,
IMSLS_RETURN_USER, &score[2][0],
0);
/* Expected value of normal order */
/* statistics using averaging to */
/* break ties */
imsls_f_ranks(N_OBSERVATIONS, x,
IMSLS_EXPECTED_NORMAL_SCORES,
IMSLS_RETURN_USER, &score[3][0],
0);
imsls_f_write_matrix("Normal Order Statistics", 4, N_OBSERVATIONS,
(float *)score,
IMSLS_ROW_LABELS, row_labels,
IMSLS_WRITE_FORMAT, "%9.3f",
0);
/* Savage scores using averaging */
/* to break ties */
ranks = imsls_f_ranks(N_OBSERVATIONS, x,
IMSLS_SAVAGE_SCORES,
0);
imsls_f_write_matrix("Expected values of exponential order "
"statistics", 1,
N_OBSERVATIONS, ranks,
0);
}
Output
Normal Order Statistics
1 2 3 4 5
Blom -1.024 0.209 -0.776 -0.294 0.473
Tukey -1.020 0.208 -0.890 -0.381 0.471
Van der Waerden -0.989 0.204 -0.753 -0.287 0.460
Expected Value -1.026 0.209 -0.836 -0.338 0.473
6 7 8 9 10
Blom -0.294 -1.610 -0.041 1.610 0.776
Tukey -0.381 -1.599 -0.041 1.599 0.773
Van der Waerden -0.372 -1.518 -0.040 1.518 0.753
Expected Value -0.338 -1.616 -0.041 1.616 0.777
11 12 13 14 15
Blom 1.176 1.361 0.041 0.668 -1.361
Tukey 1.171 1.354 0.041 0.666 -1.354
Van der Waerden 1.131 1.300 0.040 0.649 -1.300
Expected Value 1.179 1.365 0.041 0.669 -1.365
16 17 18 19 20
Blom 0.125 -0.209 -2.040 -1.176 -0.776
Tukey 0.124 -0.208 -2.015 -1.171 -0.890
Van der Waerden 0.122 -0.204 -1.849 -1.131 -0.865
Expected Value 0.125 -0.209 -2.043 -1.179 -0.836
21 22 23 24 25
Blom 1.024 0.294 -0.473 -0.125 2.040
Tukey 1.020 0.293 -0.471 -0.124 2.015
Van der Waerden 0.989 0.287 -0.460 -0.122 1.849
Expected Value 1.026 0.294 -0.473 -0.125 2.043
26 27 28 29 30
Blom 0.893 -0.568 0.382 -0.668 0.568
Tukey 0.890 -0.566 0.381 -0.666 0.566
Van der Waerden 0.865 -0.552 0.372 -0.649 0.552
Expected Value 0.894 -0.568 0.382 -0.669 0.568
Expected values of exponential order statistics
1 2 3 4 5 6
0.179 0.892 0.240 0.474 1.166 0.474
7 8 9 10 11 12
0.068 0.677 2.995 1.545 2.162 2.495
13 14 15 16 17 18
0.743 1.402 0.104 0.815 0.555 0.033
19 20 21 22 23 24
0.141 0.240 1.912 0.975 0.397 0.614
25 26 27 28 29 30
3.995 1.712 0.350 1.066 0.304 1.277
