Analyzes data from split-split-plot experiments.  The whole-plots can be assigned to experimental units using either a completely randomized or randomized complete block design.  Function split_split_plot also analyzes split-split-plot experiments replicated at several locations.

Synopsis

#include <imsls.h>

float  *imsls_f_split_split_plot (int n, int n_locations, int n_whole, int n_split, int n_sub, int rep[], int whole[], int split[], int sub[], float y[],…, 0)

The type double function is imsls_d_split_split_plot.

Required Arguments

int n  (Input)
Number of missing and non-missing experimental observations.  imsls_f_split_split_plot verifies that:

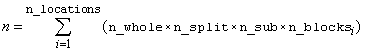
            where n_blocks_i is equal to the number of blocks or replicates at the i-th location.

int n_locations (Input)
Number of locations.  n_locations must be one or greater.   If n_locations>1 then the optional array locations[] must be included as input. See optional argument IMSLS_LOCATIONS.

int n_whole  (Input)
Number of levels associated with the whole-plot factor.  n_whole must be greater than one.

int n_split  (Input)
Number of levels associated with the split-plot factor.  n_split must be greater than one.

int n_sub  (Input)
Number of levels associated with the sub-plot factor.  n_sub must be greater than one.

int rep[]  (Input)
An array of length n containing the block, or replicate, identifiers for each observation in y.  Different locations can have different numbers of blocks or replicates.  Each block or replicate at a single location must be assigned a different identifier, but different locations can have the same assignments.

int whole[]  (Input)
An array of length n containing the whole-plot identifiers for each observation in y.  Each level of the whole-plot factor must be assigned a different integer.  imsls_f_split_split_plot verifies that the number of unique whole-plot identifiers is equal to n_whole.

int split[]  (Input)
An array of length n containing the split-plot identifiers for each observation in y.  Each level of the split-plot factor must be assigned a different integer.  imsls_f_split_split_plot verifies that the number of unique split-plot identifiers is equal to n_split.

int sub[]  (Input)
An array of length n containing the sub-plot identifiers for each observation in y.  Each level of the sub-plot factor must be assigned a different integer.  imsls_f_split_split_plot verifies that the number of unique sub-plot identifiers is equal to n_sub.

float y[] (Input)
An array of length n containing the experimental observations and any missing values.  Missing values cannot be omitted.  They are included by placing a NaN (not a number) in y. The NaN value can be set using either the function imsls_f_machine(6) or imsls_d_machine(6), depending upon whether single or double precision is being used, respectively.  At a single location, only one missing value per whole-plot is allowed.  The location, whole-plot, split-plot and sub-plot for each observation in y are identified by the corresponding values in the arguments locations, whole, split and sub.

Return Value

Address of a pointer to the memory location of a two dimensional, 20 by 6 array containing the ANOVA table.  Each row in this array contains values for one of the effects in the ANOVA table.  The first value in each row, anova_table_i,0 = anova_table[i*6], identifies the source for the effect associated with values in that row.  The remaining values in a row contain the ANOVA table values using the following convention:

 

 

The Source Identifiers in the first column of anova_table_i,j are the only negative values in anova_table[]. Note that the p-value for the F-statistic is returned as 0.0 when the value is so small that all significant digits have been lost. Assignments of identifiers to ANOVA sources use the following coding:

NOTES: † If n_locations=1 sources involving location are set to missing (NaN).

‡   If IMSLS_CRD is set, entries for blocks within location are set to missing, and  its sum of squares and degrees of freedom are pooled into the whole-plot error.

*  Split-plot error component calculation varies depending upon n_locations. See “Description” below for details.

Synopsis with Optional Arguments

#include <imsl.h>

float  *imsls_f_split_split_plot (int n, int n_locations, int n_whole,
int n_split, int n_sub, int rep[], int whole[], int split[],int sub[],
float y[],
IMSLS_RETURN_USER, float anova_table[],
IMSLS_LOCATIONS, int locations[],
IMSLS_RCBD or IMSLS_CRD,
IMSLS_N_MISSING, int *n_missing,
IMSLS_CV, float **cv,
IMSLS_CV_USER, float cv[],
IMSLS_GRAND_MEAN, float *grand_mean,
IMSLS_WHOLE_PLOT_MEANS, float **whole_plot_means,
IMSLS_WHOLE_PLOT_MEANS_USER, float whole_plot_means[],
IMSLS_SPLIT_PLOT_MEANS, float **split_plot_means,
IMSLS_SPLIT_PLOT_MEANS_USER, float split_plot_means[],
IMSLS_SUB_PLOT_MEANS, float **sub_plot_means,
IMSLS_SUB_PLOT_MEANS_USER, float sub_plot_means[],
IMSLS_WHOLE_SPLIT_PLOT_MEANS, float **whole_split_plot_means,
IMSLS_WHOLE_SPLIT_PLOT_MEANS_USER, float whole_split_plot_means[],
IMSLS_WHOLE_SUB_PLOT_MEANS, float **whole_sub_plot_means,
IMSLS_WHOLE_SUB_PLOT_MEANS_USER,float whole_sub_plot_means[],
IMSLS_SPLIT_SUB_PLOT_MEANS, float **split_sub_plot_means,
IMSLS_SPLIT_SUB_PLOT_MEANS_USER, float split_sub_plot_means[],
IMSLS_TREATMENT_MEANS, float **treatment_means,
IMSLS_TREATMENT_MEANS_USER, float treatment_means[],
IMSLS_STD_ERRORS, float **std_err,
IMSLS_STD_ERRORS_USER, float std_err[],
IMSLS_N_BLOCKS, int **n_blocks,
IMSLS_N_BLOCKS_USER, int n_blocks[],
IMSLS_LOCATION_ANOVA_TABLE float **location_anova_table,
IMSLS_LOCATION_ANOVA_TABLE_USER, float location_anova_table[],
IMSLS_ANOVA_ROW_LABELS, char ***anova_row_labels,
IMSLS_ANOVA_ROW_LABELS_USER, char *anova_row_labels[],
0)

Optional Arguments

IMSLS_RETURN_USER, float anova_table[] (Output)
User defined array of length 120 for storage of the 20 by 6 anova table described as the return argument for imsls_f_split_split_plot.  For a detailed description of the format for this table, see the previous description of the return value for imsls_f_split_split_plot.

IMSLS_LOCATIONS, int locations[]  (Input)
An array of length n containing the location identifiers for each observation in y.  Unique integers must be assigned to each location in the study.  This argument is required when n_locations>1.

IMSLS_RCBD or IMSLS_CRD (Input)
Whole-plot randomization characteristic:  IMSLS_RCBD implies that whole-plots are assigned to whole-plot experimental units using a randomized complete block design.  IMSLS_CRD implies that whole-plots are completely randomized to whole-plot experimental units.  Default: IMSLS_RCBD.

IMSLS_N_MISSING, int *n_missing  (Output)
Number of missing values, if any, found in y. Missing values are denoted with a NaN (Not a Number) value.

IMSLS_CV, float **cv (Output)
Address of a pointer to  an internally allocated array of length 3 containing the whole-plot, split-plot and sub-plot coefficients of variation.  cv[0] contains the whole-plot C.V., cv[1] contains the split-plot C.V., and cv[2] contains the sub-plot C.V.

IMSLS_CV_USER, float cv[] (Output)
Storage for the array cv, provided by the user.

IMSLS_GRAND_MEAN, float *grand_mean (Output)
Mean of all the data across every location.

IMSLS_WHOLE_PLOT_MEANS, float **whole_plot_means (Output)
 Address of a pointer to an internally allocated array of length n_whole containing the whole-plot means.

IMSLS_WHOLE_PLOT_MEANS_USER, float whole_plot_means[] (Output)
Storage for the array whole_plot_means, provided by the user.

IMSLS_SPLIT_PLOT_MEANS, float **split_plot_means (Output)
Address of a pointer to an internally allocated array of length n_split containing the split-plot means.

IMSLS_SPLIT_PLOT_MEANS_USER, float split_plot_means[] (Output)
Storage for the array split_plot_means, provided by the user.

IMSLS_SUB_PLOT_MEANS, float **sub_plot_means (Output)
 Address of a pointer to an internally allocated array of length n_sub containing the sub-plot means.

IMSLS_SUB_PLOT_MEANS_USER, float sub_plot_means[] (Output)
Storage for the array sub_plot_means, provided by the user.

IMSLS_WHOLE_SPLIT_PLOT_MEANS, float **whole_split_plot_means (Output)
 Address of a pointer to an internally allocated 2-dimensional array of size n_whole by n_split containing the whole-plot by split-plot means.

IMSLS_WHOLE_SPLIT_PLOT_MEANS_USER, float whole_split_plot_means[] (Output)
Storage for the array whole_split_plot_means, provided by the user.

IMSLS_WHOLE_SUB_PLOT_MEANS, float **whole_sub_plot_means (Output)
Address of a pointer to an internally allocated 2-dimensional array of size n_whole by  n_sub containing the whole-plot by sub-plot means.

IMSLS_WHOLE_SUB_PLOT_MEANS_USER, float whole_sub_plot_means[] (Output)
Storage for the array whole_sub_plot_means, provided by the user.

IMSLS_SPLIT_SUB_PLOT_MEANS, float **split_sub_plot_means (Output)
 Address of a pointer to an internally allocated 2-dimensional array of size n_split by n_sub containing the split-plot by sub-plot means.

IMSLS_SPLIT_SUB_PLOT_MEANS_USER, float split_sub_plot_means[] (Output)
Storage for the array split_sub_plot_means, provided by the user.

IMSLS_TREATMENT_MEANS, float **treatment_means (Output)
Address of a pointer to an internally allocated array of size (n_whole*n_strip*n_sub) containing the treatment means. For i > 0, j > 0 and  k > 0, treatment_means_i,j,k = treatment_means[(i-1)*n_sptrip*n_sub+(j-1)*n_sub + k-1] contains the mean of the observations, averaged over all locations, blocks and replicates, for the kth sub-plot within the j-th split-plot within the i-th whole-plot.

IMSLS_TREATMENT_MEANS_USER, float treatment_means[]  (Output)
Storage for the array treatment_means, provided by the user.

IMSLS_STD_ERRORS, float **std_err (Output)
 Address of a pointer to an internally allocated array of length 8 containing five standard errors and their associated degrees of freedom.   The standard errors are in the first five elements and their associated degrees of freedom are reported in std_err[4] through std_err[7].

 

IMSLS_STD_ERRORS_USER, float std_err[] (Output)
Storage for the array std_err, provided by the user.

IMSLS_N_BLOCKS, int **n_blocks (Output)
Address of a pointer to an internally allocated array of length n_locations containing the number of blocks, or replicates, at each location.

IMSLS_N_BLOCKS_USER, int n_blocks[] (Output)
Storage for the array n_blocks, provided by the user.

IMSLS_LOCATION_ANOVA_TABLE, float **location_anova_table (Output)
 Address of a pointer to an internally allocated 3-dimensional array of size n_locations  by 20 by 6 containing the anova tables associated with each location.  For each location, the 20 by 6 dimensional array corresponds to the anova table for that location.  For example, location_anova_table[(i-1)*120+(j-1)*6 + (k-1)] contains the value in the kth column and j-th row of the returned anova-table for the i-th location.

IMSLS_LOCATION_ANOVA_TABLE_USER, float anova_table[] (Output)
Storage for the array location_anova_table, provided by the user.

IMSLS_ANOVA_ROW_LABELS, char ***anova_row_labels   (Output)
Address of a pointer to a pointer to an internally allocated array containing the labels for each of the n_anova rows of the returned ANOVA table. The label for the i-th row of the ANOVA table can be printed with printf("%s", anova_row_labels[i]);

The memory associated with anova_row_labels can be freed with a single call to imsls_free(anova_row_labels).

IMSLS_ANOVA_ROW_LABELS_USER, char *anova_row_labels[]   (Output)
Storage for the array anova_row_labels, provided by the user.  The amount of space required will vary depending upon the number of factors and n_anova.  An upperbound on the required memory is char *anova_row_labels[600].

Description

Function imsls_f_split_split_plot is capable of analyzing a wide variety of split-split-plot experiments. 

Split-split-plot experimental designs can vary in the assignment of whole-plot factors to experimental units.  In some cases, this assignment is completely random.  For example, in a drug study the experimental unit might be the subject receiving a treatment.  The whole-plot factor, possibly different treatments, could be assigned in one of two ways.  Each subject could receive only one treatment or each could receive all treatments over an appropriate period of time.  If each subject received only a single randomly selected treatment, then this design constitutes a completely randomized design for the whole-plot factor, and the optional input argument IMSLS_CRD must be set. 

On the other hand, if each subject receives every treatment in random order, then the subject is a blocking factor, and this sampling scheme constitutes a randomized complete block design.  In this case, it is necessary to assume that there are no carry-over effects from one treatment to another.  This sampling scheme is the default setting, i.e. IMSLS_RCBD is the default setting.

This randomization choice occurs often in agricultural field trials.  A trial designed to test different fertilizers and different seed lots can be conducted in one of two ways.  The whole-plot factor, fertilizer, can be applied to different fields, or each can be applied to sub-divisions of these fields. In either case, a field, or a sub-division of a field, is the whole-plot experimental unit.  In the first case, in which only one randomly selected fertilizer is applied to each field, the whole-plot factor is not blocked and this scheme is called as a completely randomized design, and the optional input argument IMSLS_CRD must be set.  However, if fertilizers are applied to sub-divisions within a field, then the whole-plot factor is blocked within fields and this assignment is referred to as a randomized complete block design.  By default, imsls_f_split_split_plot assumes that levels of the whole-plot factor are randomly assigned within blocks, i.e.IMSLS_RCBD is the default setting for randomizing whole-plots.

The essential distinction between split-plot  and split-split-plot experiments is the presence of a third factor that is blocked, or nested, within each level of the whole-plot and split-plot factors.  This third factor is referred to as the sub-plot factor.

 

Table 4- 25 – Split-Plot Experiment – Split-Plot B Nested within Whole-Plot A

 

Table 4- 26 – Split-Split Plot Experiment – Sub-Plot Factor C Nested Within Split-Plot Factor B, Nested Within Whole-Plot Factor A

Contrast the split-split plot experiment to the same experiment run using a strip-split plot design, see Table 4 - 27.  In a strip-split plot experiment factor B is applied in strip across factor A; whereas, in a split-split plot experiment, factor B is randomly assigned to each level of factor A.  In a strip-split plot experiment, the level of factor B is constant across a row; whereas in a split-split plot experiment, the levels of factor B change as you go across a row, reflecting the fact that factor B is randomized within each level of factor A.

 

Table 4- 27 – Strip-Split Plot Experiment - Split-Plots Nested Within Strip-Plot Factors A and B

In some studies, a split-split-plot experiment is replicated at several locations.  Function imsls_f_split_split_plot can analyze these, even when the number of blocks or replicates at each location is different.  If only a single replicate or block is used at each location, then location should be treated as a blocking factor, with n_locations set equal to one.   If n_locations=1, it is assumed that the experiment was conducted at a single location with more than one block or replicate at that location.  In this case, all entries in the anova table associated with location will contain missing values.

However, if n_locations>1, it is assumed the experiment was repeated at multiple locations, with replication or blocking occurring at each location.  Although the number of blocks, or replicates, at each location can be different, the number of levels for whole-plot and split-plot factors, n_whole and n_split, must be the same at each location.  The locations associated with each of the observations in y are specified in the argument locations[], which is a required input argument when n_locations>1. 

By default, locations are assumed to be random effects. Tests involving whole-plots use the interaction between whole-plots and locations as the error term for testing whether there are statistically significant differences among whole-plot factor levels.  This assumes that the interaction of whole-plots and locations is not statistically significant.  A test of this assumption uses the pooled whole-plot error.  If the interaction between location and whole-plots, split-plots or sub-plot is statistically significant, then the nature of that interaction should be explored since it impacts the interpretation of the significance of the treatment factors.

When n_locations >1 are assumed to be random effects, tests involving split-plots do not use the split-plot errors pooled across locations.  Instead, the error term for split plots is the interaction between locations and split-plots.  The split-plot by whole-plot interaction is tested against the location by split-plot by whole-plot interaction. 

Suppose, for example, that a researcher wanted to conduct an agricultural experiment comparing the effectiveness of 4 fertilizers with 3 rates of application and 2 seed lots.  One replicate of the experiment is conducted at each of the 3 farms.  That is, only a single field at each location is assigned to this experiment. 

Each field is divided into 4 whole-plots and the fertilizers are randomly assigned to each of the 4 whole-plots.  Each whole-plot is then further sub-divided into 3 split-plots which are each randomly assigned one of the three fertilizer application rates.  Finally, each of these sub-divisions assigned a particular fertilizer and application rate is sub-divided into 2 plots and randomly assigned one of the two seed lots.

In this case, each farm is a blocking factor, fertilizers are whole-plots and fertilizer application rate are split plots, and seed lots are sub-plots.  The input array rep would contain integers from 1 to the number of farms, with n_whole=4, n_split=3 and n_sub=2.

However, if each farm allocated more than a single field for this study, then each farm would be treated as a different location with n_locations set equal to the number of farms, and fields might be treated as blocking factor.  The array rep would contain integers from 1 to the number fields used in a farm, and locations[] would contain integers from 1 to the number of farms.

In summary imsls_f_split_split_plot can analyze 3x2=6 different experimental situations, depending upon the settings of:

1.     Locations (none, fixed or random): specified by setting n_locations, locations[] and IMSLS_LOC_FIXED or IMSLS_LOC_RANDOM.

2.     Whole-plot sampling (CRD or RCBD): specified by setting IMSLS_CRD or IMSLS_RCBD.

The default condition depends upon the value for n_locations. If n_locations>1, locations are assumed to be a random effect.  Assignment of experimental units to whole-plots is assumed to use a RCBD design and whole-plots, split-plots and sub-plots are all assumed to be fixed effects.

Example

This example uses data from a split-split-plot design consisting of 2 whole-plots, 2-split-plots and 2 sub-plots.

 

#include <stdlib.h>

#include <stdio.h>

#include <math.h>

#include <imsls.h>

 

int main()

{

   char **anova_row_labels;

   char *col_labels[] = {" ", "\nID", "\nDF", "\nSSQ",

      "Mean\nsquares", "\nF", "\np-value"};

   char dashes[] =

      "*************************************************************";

   int i, j, k, l, page_width = 132;

 

   int n = 24;        

   int n_locations = 1;

   int n_whole = 2;   

   int n_split = 2;   

   int n_sub   = 2;

   int rep[]={

      1, 1, 1, 1, 1, 1, 1, 1,

      2, 2, 2, 2, 2, 2, 2, 2,

      3, 3, 3, 3, 3, 3, 3, 3

   };

   int whole[]={  

      1, 1, 1, 1, 2, 2, 2, 2,

      1, 1, 1, 1, 2, 2, 2, 2,

      1, 1, 1, 1, 2, 2, 2, 2

   };

   int split[]={   

      1, 1, 2, 2, 1, 1, 2, 2, f

      1, 1, 2, 2, 1, 1, 2, 2, 

      1, 1, 2, 2, 1, 1, 2, 2

   };

   int sub[]={   

      1, 2, 1, 2, 1, 2, 1, 2,

      1, 2, 1, 2, 1, 2, 1, 2, 

      1, 2, 1, 2, 1, 2, 1, 2

   };

   float y[] ={   

      30.0, 40.0, 38.9, 38.2,

      41.8, 52.2, 54.8, 58.2,

      20.5, 26.9, 21.4, 25.1,

      26.4, 36.7, 28.9, 35.9,

      21.0, 25.4, 24.0, 23.3,

      34.4, 41.0, 33.0, 34.9

   };

   float grand_mean, *cv, *aov, *treatment_means;

   float *whole_plot_means, *split_plot_means;

   float *sub_plot_means, *std_err;

   int   *equal_means; 

 

   aov = imsls_f_split_split_plot(n, n_locations, n_whole, n_split,

      n_sub, rep, whole, split, sub, y,

      IMSLS_GRAND_MEAN, &grand_mean,

      IMSLS_CV, &cv,

      IMSLS_TREATMENT_MEANS,  &treatment_means,

      IMSLS_WHOLE_PLOT_MEANS, &whole_plot_means,

      IMSLS_SPLIT_PLOT_MEANS, &split_plot_means,

      IMSLS_SUB_PLOT_MEANS,   &sub_plot_means,

      IMSLS_STD_ERRORS,       &std_err,

      IMSLS_ANOVA_ROW_LABELS, &anova_row_labels,

      0);

 

   /* Output results. */

   imsls_page(IMSLS_SET_PAGE_WIDTH, &page_width);

 

   /* Print ANOVA table. */

   imsls_f_write_matrix("   *** ANALYSIS OF VARIANCE TABLE ***",

      20, 6, aov,

      IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.2f%7.2f%7.2f%7.3f",

      IMSLS_ROW_LABELS, anova_row_labels,

      IMSLS_COL_LABELS, col_labels,

      0);

 

   printf("\n\nGrand mean:    %7.3f\n", grand_mean);

   printf("Coefficient of Variation ****\n");

   printf("  Whole-Plot: %7.3f\n", cv[0]);

   printf("  Split-Plot: %7.3f\n", cv[1]);

   printf("  Sub-Plot  : %7.3f\n", cv[2]);

   l = 0;

   /*

   * Treatment Means

   */

   printf("\n\n%s\n", dashes);

   printf("Treatment Means: \n");

   for (i=0; i < n_whole; i++){

      for(j=0; j < n_split; j++){

         for(k=0; k < n_sub; k++){

            printf("  treatment[%d][%d][%d] %f \n", i, j, k,

               treatment_means[l++]);

         }

      }

   }

   printf("\n  Standard Error for Comparing Two Treatment Means: %f ",

      std_err[3]);

   printf("\n(df=%f)\n", std_err[7]);

   equal_means = imsls_f_multiple_comparisons(n_whole*n_split*n_sub,

      treatment_means, (int)std_err[7],

      std_err[3]/sqrt(2),

      IMSLS_LSD,

      IMSLS_ALPHA, .05,

      0);

   printf("\n  LSD for Treatment Means (alpha=0.05)");

   imsls_i_write_matrix("  Size of Groups of Means", 1,

      n_whole*n_split*n_sub-1, equal_means, 0);

   /*

   * Whole-plot Means

   */

   printf("\n\n%s", dashes);

   imsls_f_write_matrix("Whole-plot Means", n_whole, 1,

      whole_plot_means, 0);

   printf("\nStandard Error for Comparing Two Whole-Plot Means: %f ",

      std_err[0]);

   printf("\n(df=%f)\n", std_err[4]);

   equal_means = imsls_f_multiple_comparisons(n_whole,

      whole_plot_means, (int)std_err[4], std_err[0]/sqrt(2),

      IMSLS_LSD,

      IMSLS_ALPHA, .05,

      0);

   printf("\nLSD for Whole-Plot Means (alpha=0.05) \n");

   imsls_i_write_matrix("Size of Groups of Means", 1, n_whole-1,

      equal_means, 0);

   /*

   * Split-plot Means

   */

   printf("\n\n%s",dashes);

   imsls_f_write_matrix("Split-plot Means", n_split, 1,

      split_plot_means, 0);

   printf("\nStandard Error for Comparing Two Split-Plot Means: %f ",

      std_err[1]);

   printf("\n(df=%f)\n", std_err[5]);

   equal_means = imsls_f_multiple_comparisons(n_split,

      split_plot_means, (int)std_err[5], std_err[1]/sqrt(2),

      IMSLS_LSD,

      IMSLS_ALPHA, .05,

      0);

   printf("\nLSD for Split-Plot Means (alpha=0.05) \n");

   imsls_i_write_matrix("Size of Groups of Means", 1, n_split-1,

      equal_means, 0);

   /*

   * Sub-plot Means

   */

   printf("\n\n%s", dashes);

   imsls_f_write_matrix("Sub-plot Means", n_sub, 1, sub_plot_means, 0);

   printf("\nStandard Error for Comparing Two Sub-Plot Means: %f ",

      std_err[2]);

   printf("\n(df=%f)\n", std_err[6]);

   equal_means = imsls_f_multiple_comparisons(n_sub, sub_plot_means,

      (int)std_err[6], std_err[2]/sqrt(2),

      IMSLS_LSD,

      IMSLS_ALPHA, .05,

      0);

   printf("\nLSD for Sub-Plot Means (alpha=0.05) \n");

   imsls_i_write_matrix(": Size of Groups of Means", 1, n_sub-1,

      equal_means, 0);

}

 

Output

                        *** ANALYSIS OF VARIANCE TABLE ***

                                                         Mean

                                   ID   DF       SSQ  squares        F  p-value

Location                           -1  ...  ........  .......  .......  .......

Blocks Within Location             -2    2   1310.28   655.14    30.82    0.031

Whole-Plot                         -3    1    858.01   858.01    40.37    0.024

Location x Whole-Plot              -4  ...  ........  .......  .......  .......

Whole-Plot Error                   -5    2     42.51    21.26     0.86    0.490

Split-Plot                         -6    1     17.17    17.17     0.69    0.452

Location x Split-Plot              -7  ...  ........  .......  .......  .......

Whole-Plot x Split-Plot            -8    1      1.55     1.55     0.06    0.815

Location x Whole-Plot x            -9  ...  ........  .......  .......  .......

   Split-Plot

Split-Plot Error                  -10    4     99.32    24.83     7.62    0.008

Sub-Plot                          -11    1    163.80   163.80    50.27    0.000

Location x Sub-Plot               -12  ...  ........  .......  .......  .......

Whole-Plot x Sub-Plot             -13    1     11.34    11.34     3.48    0.099

Location x Whole-Plot x Sub-Plot  -14  ...  ........  .......  .......  .......

Split-plot x Sub-Plot             -15    1     46.76    46.76    14.35    0.005

Location x Split-Plot x Sub-Plot  -16  ...  ........  .......  .......  .......

Whole_plot x Split-Plot           -17    1      0.51     0.51     0.16    0.703

   x Sub-Plot

Location x Whole-Plot x           -18  ...  ........  .......  .......  .......

   Split-Plot x Sub-Plot

Sub-Plot Error                    -19    8     26.07     3.26  .......  .......

Corrected Total                   -20   23   2577.33  .......  .......  .......

 

 

Grand mean:     33.871

Coefficient of Variation ****

  Whole-Plot:  13.612

  Split-Plot:  14.712

  Sub-Plot  :   5.329

 

 

*************************************************************

Treatment Means:

  treatment[0][0][0] 23.833334

  treatment[0][0][1] 30.766668

  treatment[0][1][0] 28.100000

  treatment[0][1][1] 28.866669

  treatment[1][0][0] 34.200001

  treatment[1][0][1] 43.299999

  treatment[1][1][0] 38.899998

  treatment[1][1][1] 43.000000

 

  Standard Error for Comparing Two Treatment Means: 1.473846

(df=8.000000)

 

  LSD for Treatment Means (alpha=0.05)

   Size of Groups of Means

 1   2   3   4   5   6   7

 0   3   0   0   0   0   2

 

 

*************************************************************

Whole-plot Means

 1        27.89

 2        39.85

 

Standard Error for Comparing Two Whole-Plot Means: 2.661792

(df=2.000000)

 

LSD for Whole-Plot Means (alpha=0.05)

 

Size of Groups of Means

           0

 

 

*************************************************************

Split-plot Means

 1        33.03

 2        34.72

 

Standard Error for Comparing Two Split-Plot Means: 2.876944

(df=4.000000)

 

LSD for Split-Plot Means (alpha=0.05)

 

Size of Groups of Means

           2

 

 

*************************************************************

Sub-plot Means

1        31.26

2        36.48

 

Standard Error for Comparing Two Sub-Plot Means: 1.473846

(df=8.000000)

 

LSD for Sub-Plot Means (alpha=0.05)

 

: Size of Groups of Means

            0

---

Contact Support