FPS3H
Solves Poisson’s or Helmholtz’s equation on a three-dimensional box using a fast Poisson solver based on the HODIE finite-difference scheme on a uniform mesh.
Required Arguments
PRHS — User-supplied FUNCTION to evaluate the right side of the partial differential equation. The form is PRHS(X, Y, Z), where
X – The x-coordinate value. (Input)
Y – The y-coordinate value. (Input)
Z – The z-coordinate value. (Input)
PRHS – Value of the right side at (X, Y, Z). (Output)
PRHS must be declared EXTERNAL in the calling program.
BRHS — User-supplied FUNCTION to evaluate the right side of the boundary conditions. The form is BRHS(ISIDE, X, Y, Z), where
ISIDE – Side number. (Input)
See IBCTY for the definition of the side numbers.
X – The x-coordinate value. (Input)
Y – The y-coordinate value. (Input)
Z – The z-coordinate value. (Input)
BRHS – Value of the right side of the boundary condition at (X, Y, Z). (Output)
BRHS must be declared EXTERNAL in the calling program.
COEFU — Value of the coefficient of U in the differential equation. (Input)
NX — Number of grid lines in the x-direction. (Input)
NX must be at least 4. See Comment 2 for further restrictions on NX.
NX must be at least 4. See Comment 2 for further restrictions on NX.
NY — Number of grid lines in the y-direction. (Input)
NY must be at least 4. See Comment 2 for further restrictions on NY.
NY must be at least 4. See Comment 2 for further restrictions on NY.
NZ — Number of grid lines in the z-direction. (Input)
NZ must be at least 4. See Comment 2 for further restrictions on NZ.
NZ must be at least 4. See Comment 2 for further restrictions on NZ.
AX — Value of X along the left side of the domain. (Input)
BX — Value of X along the right side of the domain. (Input)
AY — Value of Y along the bottom of the domain. (Input)
BY — Value of Y along the top of the domain. (Input)
AZ — Value of Z along the front of the domain. (Input)
BZ — Value of Z along the back of the domain. (Input)
IBCTY — Array of size 6 indicating the type of boundary condition on each face of the domain or that the solution is periodic. (Input)
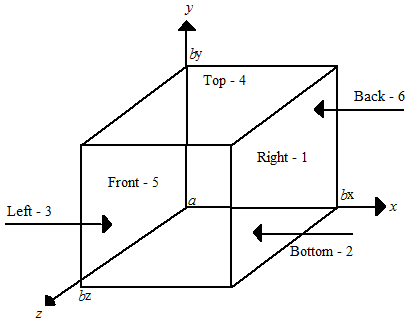
The sides are numbers 1 to 6 as follows:
The sides are numbers 1 to 6 as follows:
Side | Location |
|---|---|
1 - Right | (X = BX) |
2 - Bottom | (Y = AY) |
3 - Left | (X = AX) |
4 - Top | (Y = BY) |
5 - Front | (Z = BZ) |
6 - Back | (Z = AZ) |
There are three boundary condition types.
IBCTY | Boundary Condition |
|---|---|
1 | Value of U is given. (Dirichlet) |
2 | Value of dU/dX is given (sides 1 and/or 3). (Neumann) Value of dU/dY is given (sides 2 and/or 4). Value of dU/dZ is given (sides 5 and/or 6). |
3 | Periodic. |
U — Array of size NX by NY by NZ containing the solution at the grid points. (Output)
Optional Arguments
IORDER — Order of accuracy of the finite-difference approximation. (Input)
It can be either 2 or 4. Usually, IORDER = 4 is used.
Default: IORDER = 4.
It can be either 2 or 4. Usually, IORDER = 4 is used.
Default: IORDER = 4.
LDU — Leading dimension of U exactly as specified in the dimension statement of the calling program. (Input)
Default: LDU = size (U,1).
Default: LDU = size (U,1).
MDU — Middle dimension of U exactly as specified in the dimension statement of the calling program. (Input)
Default: MDU = size (U,2).
Default: MDU = size (U,2).
FORTRAN 90 Interface
Generic: CALL FPS3H (PRHS, BRHS, COEFU, NX, NY, NZ, AX, BX, AY, BY, AZ, BZ, IBCTY, U [, …])
Specific: The specific interface names are S_FPS3H and D_FPS3H.
FORTRAN 77 Interface
Single: CALL FPS3H (PRHS, BRHS, COEFU, NX, NY, NZ, AX, BX, AY, BY, AZ, BZ, IBCTY, IORDER, U, LDU, MDU)
Double: The double precision name is DFPS3H.
Description
Let c = COEFU, ax = AX, bx = BX, nx = NX, ay = AY, by = BY, ny = NY, az = AZ, bz = BZ, and nz = NZ.
FPS3H is based on the code HFFT3D by Boisvert (1984). It solves the equation
on the domain (ax, bx) × (ay, by) × (az, bz) (a box) with a user-specified combination of Dirichlet (solution prescribed), Neumann (first derivative prescribed), or periodic boundary conditions. The six sides are numbered as shown in the following diagram.
When c = 0 and only Neumann or periodic boundary conditions are prescribed, then any constant may be added to the solution to obtain another solution to the problem. In this case, the solution of minimum∞‑norm is returned.
The solution is computed using either a second-or fourth-order accurate finite-difference approximation of the continuous equation. The resulting system of linear algebraic equations is solved using fast Fourier transform techniques. The algorithm relies upon the fact that nx ‑ 1 and nz ‑ 1 are highly composite (the product of small primes). For details of the algorithm, see Boisvert (1984). If nx ‑ 1 and nz ‑ 1 are highly composite, then the execution time of FPS3H is proportional to
If evaluations of p(x, y, z) are inexpensive, then the difference in running time between IORDER = 2 and IORDER = 4 is small.
Comments
1. Workspace may be explicitly provided, if desired, by use of F2S3H/DF2S3H. The reference is:
CALL F2S3H (PRHS, BRHS, COEFU, NX, NY, NZ, AX, BX, AY, BY, AZ, BZ, IBCTY, IORDER, U, LDU, MDU, UWORK, WORK)
The additional arguments are as follows:
UWORK — Work array of size NX + 2 by NY + 2 by NZ + 2. If the actual dimensions of U are large enough, then U and UWORK can be the same array.
WORK — Work array of length (NX + 1)(NY + 1)(NZ + 1)(IORDER ‑ 2)/2 + 2(NX * NY + NX * NZ + NY * NZ) + 2(NX + NY + 1) + MAX(2 * NX * NY, 2 * NX + NY + 4 * NZ + (NX + NZ)/2 + 29)
2. The grid spacing is the distance between the (uniformly spaced) grid lines. It is given by the formulas
HX = (BX ‑ AX)/(NX ‑ 1),
HY = (BY ‑ AY)/(NY ‑ 1), and
HZ = (BZ ‑ AZ)/(NZ ‑ 1).
The grid spacings in the X, Y and Z directions must be the same, i.e., NX, NY and NZ must be such that HX = HY = HZ. Also, as noted above, NX, NY and NZ must all be at least 4. To increase the speed of the Fast Fourier transform, NX ‑ 1 and NZ ‑ 1 should be the product of small primes. Good choices for NX and NZ are 17, 33 and 65.
3. If -COEFU is nearly equal to an eigenvalue of the Laplacian with homogeneous boundary conditions, then the computed solution might have large errors.
Example
This example solves the equation
with the boundary conditions ∂u/∂z = ‑2 sin(3x + y ‑ 2z) ‑ exp(x ‑ z) on the front side and u = cos(3x + y ‑ 2z) + exp(x ‑z) + 1 on the other five sides. The domain is the box [0, 1/4] × [0, 1/2] × [0, 1/2]. The output of FPS3H is a 9 × 17 × 17 table of U values. The quadratic interpolation routine QD3VL is used to print a table of values.
USE FPS3H_INT
USE UMACH_INT
USE QD3VL_INT
IMPLICIT NONE
! SPECIFICATIONS FOR PARAMETERS
INTEGER LDU, MDU, NX, NXTABL, NY, NYTABL, NZ, NZTABL
PARAMETER (NX=5, NXTABL=4, NY=9, NYTABL=3, NZ=9, &
NZTABL=3, LDU=NX, MDU=NY)
!
INTEGER I, IBCTY(6), IORDER, J, K, NOUT
REAL AX, AY, AZ, BRHS, BX, BY, BZ, COEFU, FLOAT, PRHS, &
U(LDU,MDU,NZ), UTABL, X, ERROR, TRUE, &
XDATA(NX), Y, YDATA(NY), Z, ZDATA(NZ)
INTRINSIC COS, EXP, FLOAT
EXTERNAL BRHS, PRHS
! Define domain
AX = 0.0
BX = 0.125
AY = 0.0
BY = 0.25
AZ = 0.0
BZ = 0.25
! Set boundary condition types
IBCTY(1) = 1
IBCTY(2) = 1
IBCTY(3) = 1
IBCTY(4) = 1
IBCTY(5) = 2
IBCTY(6) = 1
! Coefficient of U
COEFU = 10.0
! Order of the method
IORDER = 4
! Solve the PDE
CALL FPS3H (PRHS, BRHS, COEFU, NX, NY, NZ, AX, BX, AY, BY, AZ, &
BZ, IBCTY, U)
! Set up for quadratic interpolation
DO 10 I=1, NX
XDATA(I) = AX + (BX-AX)*FLOAT(I-1)/FLOAT(NX-1)
10 CONTINUE
DO 20 J=1, NY
YDATA(J) = AY + (BY-AY)*FLOAT(J-1)/FLOAT(NY-1)
20 CONTINUE
DO 30 K=1, NZ
ZDATA(K) = AZ + (BZ-AZ)*FLOAT(K-1)/FLOAT(NZ-1)
30 CONTINUE
! Print the solution
CALL UMACH (2, NOUT)
WRITE (NOUT,'(8X,5(A,11X))') 'X', 'Y', 'Z', 'U', 'Error'
DO 60 K=1, NZTABL
DO 50 J=1, NYTABL
DO 40 I=1, NXTABL
X = AX + (BX-AX)*FLOAT(I-1)/FLOAT(NXTABL-1)
Y = AY + (BY-AY)*FLOAT(J-1)/FLOAT(NYTABL-1)
Z = AZ + (BZ-AZ)*FLOAT(K-1)/FLOAT(NZTABL-1)
UTABL = QD3VL(X,Y,Z,XDATA,YDATA,ZDATA,U, CHECK=.false.)
TRUE = COS(3.0*X+Y-2.0*Z) + EXP(X-Z) + 1.0
ERROR = UTABL - TRUE
WRITE (NOUT,'(5F12.4)') X, Y, Z, UTABL, ERROR
40 CONTINUE
50 CONTINUE
60 CONTINUE
END
!
REAL FUNCTION PRHS (X, Y, Z)
REAL X, Y, Z
!
REAL COS, EXP
INTRINSIC COS, EXP
! Right side of the PDE
PRHS = -4.0*COS(3.0*X+Y-2.0*Z) + 12*EXP(X-Z) + 10.0
RETURN
END
!
REAL FUNCTION BRHS (ISIDE, X, Y, Z)
INTEGER ISIDE
REAL X, Y, Z
!
REAL COS, EXP, SIN
INTRINSIC COS, EXP, SIN
! Boundary conditions
IF (ISIDE .EQ. 5) THEN
BRHS = -2.0*SIN(3.0*X+Y-2.0*Z) - EXP(X-Z)
ELSE
BRHS = COS(3.0*X+Y-2.0*Z) + EXP(X-Z) + 1.0
END IF
RETURN
END
Output
X Y Z U Error
0.0000 0.0000 0.0000 3.0000 0.0000
0.0417 0.0000 0.0000 3.0348 0.0000
0.0833 0.0000 0.0000 3.0558 0.0001
0.1250 0.0000 0.0000 3.0637 0.0001
0.0000 0.1250 0.0000 2.9922 0.0000
0.0417 0.1250 0.0000 3.0115 0.0000
0.0833 0.1250 0.0000 3.0175 0.0000
0.1250 0.1250 0.0000 3.0107 0.0000
0.0000 0.2500 0.0000 2.9690 0.0001
0.0417 0.2500 0.0000 2.9731 0.0000
0.0833 0.2500 0.0000 2.9645 0.0000
0.1250 0.2500 0.0000 2.9440 -0.0001
0.0000 0.0000 0.1250 2.8514 0.0000
0.0417 0.0000 0.1250 2.9123 0.0000
0.0833 0.0000 0.1250 2.9592 0.0000
0.1250 0.0000 0.1250 2.9922 0.0000
0.0000 0.1250 0.1250 2.8747 0.0000
0.0417 0.1250 0.1250 2.9211 0.0010
0.0833 0.1250 0.1250 2.9524 0.0010
0.1250 0.1250 0.1250 2.9689 0.0000
0.0000 0.2500 0.1250 2.8825 0.0000
0.0417 0.2500 0.1250 2.9123 0.0000
0.0833 0.2500 0.1250 2.9281 0.0000
0.1250 0.2500 0.1250 2.9305 0.0000
0.0000 0.0000 0.2500 2.6314 -0.0249
0.0417 0.0000 0.2500 2.7420 -0.0004
0.0833 0.0000 0.2500 2.8112 -0.0042
0.1250 0.0000 0.2500 2.8609 -0.0138
0.0000 0.1250 0.2500 2.7093 0.0000
0.0417 0.1250 0.2500 2.8153 0.0344
0.0833 0.1250 0.2500 2.8628 0.0237
0.1250 0.1250 0.2500 2.8825 0.0000
0.0000 0.2500 0.2500 2.7351 -0.0127
0.0417 0.2500 0.2500 2.8030 -0.0011
0.0833 0.2500 0.2500 2.8424 -0.0040
0.1250 0.2500 0.2500 2.8735 -0.0012
Published date: 03/19/2020
Last modified date: 03/19/2020